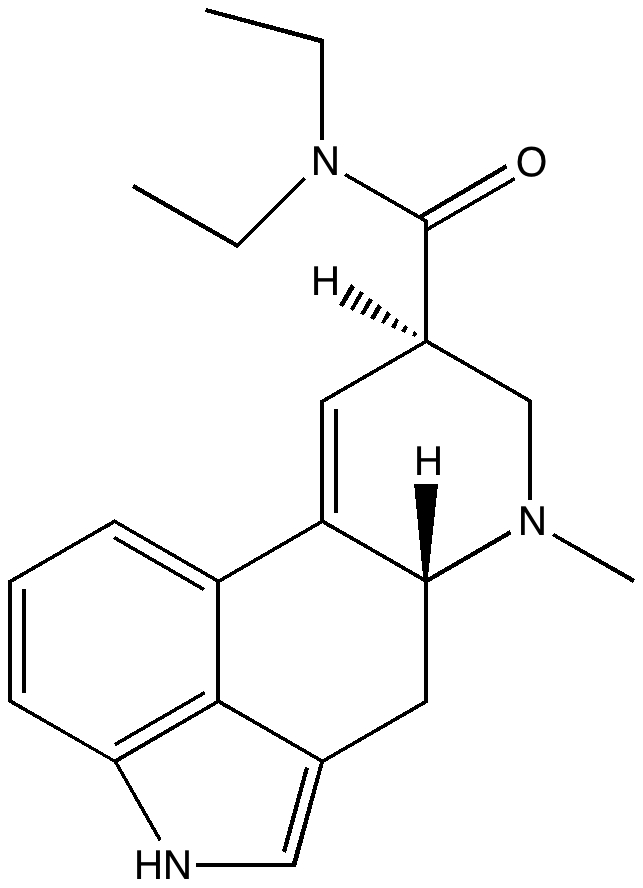
Moore’s law describes a long-term trend in the evolution of computing hardware, and it is often interpreted in terms of processing speed. Here I chart this rise in terms of the size of computable molecules. By computable I mean specifically how long it takes to predict the geometry of a given molecule using a quantum mechanical procedure.
The geometry (shape) of a molecule is defined by 3N-6 variables, where N is the number of atoms it contains. Optimising the value of variables in order to obtain the minimum value of a function was first conducted by chemical engineers, who needed to improve the function of chemical reactor plants. The mathematical techniques they developed were adopted to molecules in the 1970s, and in 1975 a milestone was reached with the molecule above. Here, N=49, and 3N-6=141. The function used was one describing its computed enthalpy of formation, using a quantum mechanical procedure known as MINDO/3. The computer used was what passed then for a supercomputer, a CDC 6600 (of which a large well endowed university could probably afford one of). It was almost impossible to get exclusive access to such a beast (its computing power was shared amongst the entire university, in this case of about 50,000 people), but during a slack period over a long weekend, the optimised geometry of LSD was obtained (it’s difficult to know how many hours the CDC 6600 took to perform this feat, but I suspect it might have been around 72). The result was announced by Paul Weiner to the group I was then part of (the Dewar research group), and Michael immediately announced that this deserved an unusual Monday night sojourn to the Texas Tavern, where double pitchers of beer would be available. You might be tempted to ask what the reason for the celebration was. Well, LSD was a “real molecule” (and not a hallucination). It meant one could predict for the first time the geometry of realistic molecules such as drugs and hence be taken seriously by people who dealt with molecules of this size for a living. And if you could predict the energy of its equilibrium geometry, you could then quickly move on to predicting the barriers to its reaction. A clear tipping point had been reached in computational simulation.
In 1975, MINDO/3 was thought to compute an energy function around 1000 to 10,000 faster than the supposedly more accurate ab initio codes then available (in fact you could not then routinely optimise geometries with the common codes of this type). With this in mind, one can subject the same molecule to a modern ωB97XD/6-311G(d,p) optimisation. This level of theory is probably closer to 104 to 105 times slower to compute than MINDO/3. On a modest “high performance” resource (which nowadays runs in parallel, in fact on 32 cores in this case), the calculation takes about an hour (starting from a 1973 X-ray structure, which turns out to be quite a poor place to start from, and almost certainly poorer than the 1975 point). In (very) round numbers, the modern calculation is about a million times faster. Which (coincidentally) is approximately the factor predicted by Moore’s law.
I will give one more example, this time for an example dating from around 2003, 28 years on from the original benchmark.
This example has 114 atoms, and hence 3N-6 =336, or 2.42 times the 1975 size. It is a transition state, which is a far slower calculation then an equilibrium geometry. It is also typical of the polymerisation chemistry of the naughties. Each run on the computer (B3LYP/6-31G(d), with the alkyl groups treated at STO-3G) now took about 8-10 days (on a machine with 4 cores), and probably 2-4 runs in total would have been required per system (of which four needed to be studied to derive meaningful conclusions). Let us say 1000 hours per transition state. Together with false starts etc, the project took about 18 months to complete. Move on to 2010; added to the model was a significantly better (= slower) basis set and a solvation correction, and a single calculation now took 67 hours. In 2011, it would be reduced to ~10 hours (by now we are up to 64-core computers).
In 2011, calculations involving ~250 atoms are now regarded as almost routine, and molecules with up to this number of atoms cover most of the discrete (i.e. non repeating) molecular systems of interest nowadays. But the 1975 LSD calculation still stands as the day that realistic computational chemistry came of age.
Tags: 3g, chemical engineers, chemical reactor plants, computational chemistry, energy, energy function, hallucination, Historical, Interesting chemistry, LSD, molecular systems, Paul Weiner, simulation, sojourn, Texas Tavern, X-ray