The discussion appended to the post on curly arrows is continued here. Recollect the curly arrow diagram (in modern style) derived from Robinson’s original suggestion:
The pertinent point is that the angle subtended at the nitrogen atom evolves from being bent (~115°) on the left, to linear (180°) on the right. The nitrogen hybridisation changes from trigonal (sp2) to digonal (sp). Because of this, the scheme must represent a reaction rather than a resonance. What kind of species is the molecule on the right? A ωB97XD/6-311G(d,p) solution of the wave equation indicates it is a transition state. The normal mode indicates that the nitrogen atom is moving out of the plane of the ring, evolving the C=N double bond back into having a nitrogen lone pair, and apparently on the way to a most interesting non-planar valence-bond isomer of nitrosobenzene. You might have noticed a nitro group has appeared in the 4-position. I did this to try to stabilize the negative charge in this position shown on the right above to prevent it from being a transition state; this subterfuge failed!
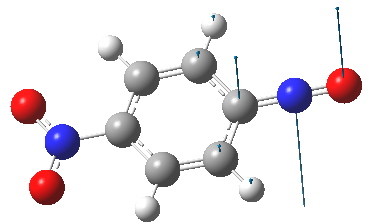
The linear form is a transition state. Click for 3D
What about an IRC (intrinsic reaction coordinate)? It starts off downhill from the transition state at IRC = 0.0. To quote Monty Python, and now for something completely different. At IRC 2.65, something does indeed happen, a most unusual feature in potential energy surfaces; a bifurcation point.
I am going to have to explain this. Normally, a transition state (a saddle point of order 1) connects two minima. But a bifurcation means that one transition state leads directly downhill (without any intervening minima) to another transition state. When the lower energy transition state is reached, the potential bifurcates, since it now has two (equal) directions for it to continue its downhill descent. Our IRC at this point has to somehow chose which of these two to take. In fact the choice is made randomly. To be precise, small so-called round-off errors in computing the derivatives of the path favour by a tiny tiny margin one of the pathways over the other, and so off it heads. As you can see below, this second pathway involves an (anticlockwise) rotation of the nitroso group (it could also have chosen clockwise).
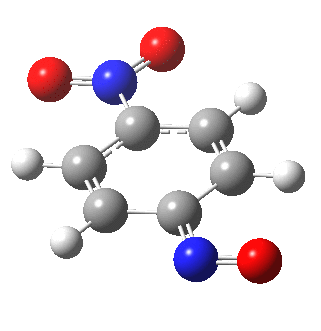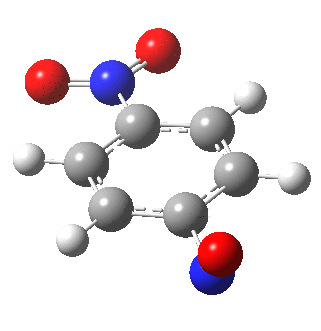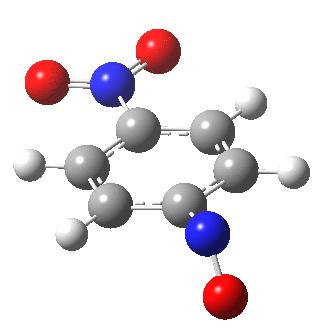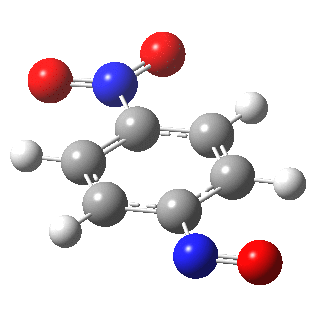
That rotation can now be represented by the following.
I continue to be surprised at where we have arrived at from Robinson’s original curly arrows; bifurcated potential energy surfaces. Well, that introductory student tutorial to curly arrow pushing is going to have to cover a lot of ground!
[qrcode content=”Robinson” size=”200″ alt=”QRCode” class=”CLASS_NAME” align=”right”]
Tags: lower energy transition state, Monty Python, nitro, potential energy surfaces, Reaction Mechanism, Tutorial material
[…] and valley-ridge inflexion points. You might not have heard of this last one, but in fact I mentioned the phenomenon in my post on nitrosobenzene. As for being at a crossroads, more like a […]
[…] but not annotated as per above! What you do find (and with Barton as well) is essentially modern use of the arrow pushing conventions, so by this period it was thoroughly […]