In a comment appended to an earlier post, I mused about the magnitude of the force constant relating to the interconversion between a classical and a non-classical structure for the norbornyl cation. Most calculations indicate the force constant for an “isolated” symmetrical cation is +ve, which means it is a true minimum and not a transition state for a [1,2] shift. The latter would have been required if the species equilibrated between two classical carbocations. I then pondered what might happen to both the magnitude and the sign of this force constant if various layers of solvation and eventually a counter-ion were to be applied to the molecule, so that a bridge of sorts between the different states of solid crystals, superacid and aqueous solutions might be built.
I augmented the model in stages. The results are summarised in the table below.
- Firstly, adding a self-consistent-reaction-field (SCRF) continuum model for water.
- Then adding to that four explicit water molecules symmetrically arranged around the four C-H groups mostly likely to be solvated via hydrogen bonds.
- The final model added a chloride anion to complete the ion pair and a further three water molecules to act as its solvation sphere. A search of the Cambridge structure database for any instances of a molecule with a designated C+ and a nucleophilic halide– with zero coordination number (a free halide anion) reveals no hits; such ion-pairs are clearly very unstable towards covalent bond formation, existing if at all only as transient species or when the counter-ion is non-nucleophilic such as R4B–.
| Calculated geometries, Def2-TZVPP/SCRF=water | ||||
|---|---|---|---|---|
|
Model |
Apical C-C distance,Å |
Basal C-C distance,Å |
ν [1,2] cm-1 |
DataDOI |
| Vacuum, cation B3LYP+D3BJ |
1.888 | 1.388 | +140 | 10.14469/hpc/2410 |
| Vacuum, cation ωB97XD |
1.830 | 1.388 | +235 | 10.14469/hpc/2409 |
| Vacuum, cation B2PLYPD3 |
1.872 | 1.390 | +194 | 10.14469/hpc/2238 |
| Vacuum, cation CCSD |
1.845 | 1.389 | — | 10.14469/hpc/2441 |
| SCRF, cation ωB97XD |
1.819 | 1.387 | +236 | 10.14469/hpc/2413 |
| SCRF, cation B2PLYPD3 |
1.858 | 1.388 | +202 | 10.14469/hpc/2243 |
| SCRF, cation CCSD |
1.833 | 1.387 | — | 10.14469/hpc/2441 |
| SCRF+4H2O, cation B2PLYPD3 |
1.838 | 1.390 | +254 | 10.14469/hpc/2246 |
| SCRF+7H2O+Cl– ion pair B3LYP+D3BJ |
1.593, 2.485 | 1.510 | – | 10.14469/hpc/2408 10.14469/hpc/2439 |
| SCRF+7H2O+Cl– ion pair ωB97XD |
1.795, 1.817 | 1.385 | +249† | 10.14469/hpc/2411 |
| SCRF+8H2O+Cl– ion pair ωB97XD |
1.771, 1.822 | 1.388 | +249† | 10.14469/hpc/2468 |
| SCRF+8H2O+Cl– ion pair MN15 |
1.756, 1.822 | 1.390 | +266† | 10.14469/hpc/2452 |
†246 cm-1 when refactored mass-weighting eliminates mode mixing between this mode and the surrounding water/chloride molecules, as shown below:
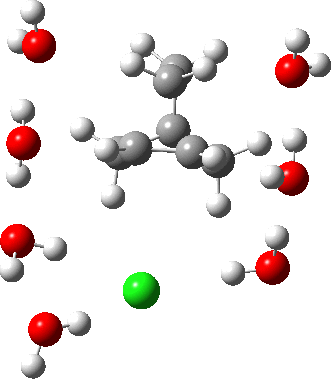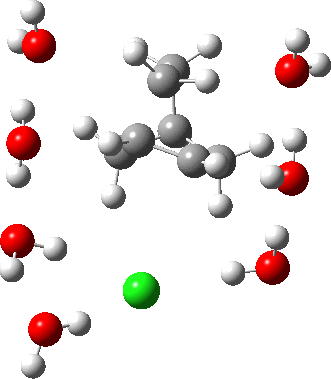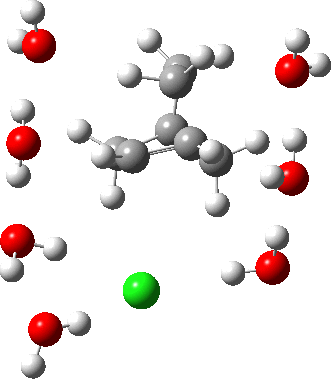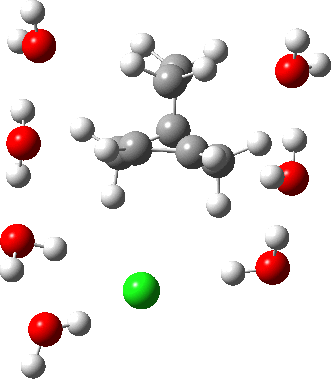
As the solvation and environment of the cationic model improves, the apical distance shortens significantly. But the crunch comes when a chloride counter-anion is added to desymmetrise this environment. Using the veritable B3LYP functional, but with an added dispersion term (D3BJ) and starting from a partially optimised ion-pair geometry, this geometry optimisation (shown animated below) rapidly quenches the ion-pair to form a covalent norbornyl chloride. It is noteworthy that the magnitude of the [1,2] vibration force constant (≡140 cm-1) is rather smaller using B3LYP than the other methods explored.
The next method tried was ωB97XD, which contains a built-in dispersion term (D2) and also reveals a larger force constant for the gas phase [1,2] shift (≡235 cm-1). Starting from the same initial geometry as the B3LYP calculation, optimisation of the ion-pair proceeds remarkably slowly‡ (even using the recalcfc=5 keyword to recompute the force constant matrix/search direction every five cycles to improve behaviour), suggesting that the potential energy surface is very flat indeed. The final geometry retains the ion-pair character (dipole moment 23D) but reveals distinct asymmetry in the resulting bridged structure, for which the [1,2] shift is ν 249 cm-1.
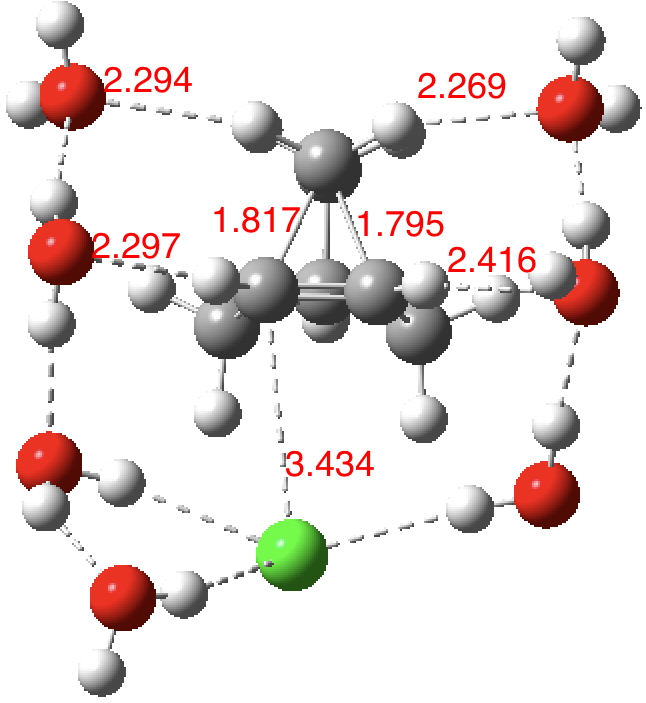
It is clear that the structure of the norbornyl ion-pair is balanced on a knife-edge. Perturbations such as change of density functional (e.g. B3LYP+D3BJ) can topple it over that edge. Weaker asymmetry can also be induced by the presence of the contact-anion and water molecules. I have selected just one solvation model, which includes seven water molecules and an explicit anion. Clearly a more statistical and dynamical approach to the number of waters and their orientation around the norbornyl ring system would sample a much larger set of models. It may be that some of them do again topple the symmetric bridge structure off its delicate perch whilst others retain it. Perhaps this is why the results from the enormous range of solvolysis mechanisms are so difficult to always reconcile. A crystal structure may also be a relatively large perturbation to the solution structure of this species!
The title of one of the last articles published (posthumously) with Paul Schleyer as a co-author[cite]10.1021/bk-2015-1209.ch007[/cite] is “Norbornyl Cation Isomers Still Fascinate“. True indeed.
‡This renders refinement using the B2PLYPD3 double-hybrid method[cite]10.1021/ct100466k[/cite] an exceptionally slow process, since computing the force constant matrix using this method is very computationally intensive at the selected triple-ζ level. This calculation uses a ωB97XD force constant matrix as a seed for the optimisation (DOI: 10.14469/hpc/2424) with the result of a collapse of the ion-pair, as was also observed using the B3LYP-D3BJ functional.
Tags: Carbocations, chemical bonding, Chemistry, constant matrix/search direction, continuum model for water, gas phase, Paul Schleyer, Physical organic chemistry, potential energy surface, Reactive intermediates, superacid and aqueous solutions
Henry, Great post! I am still fascinated by the norbornyl cation. You might find this paper of interest – DOI: 10.1021/jo701526x – not counterions but other species breaking symmetry.
Thanks Dean!
To bring others up to speed, the study involved positioning an ammonia or benzene molecule at various positions around the norbornyl cation and looking at the interaction energy computed using b3lyp/6-31+g(d,p) (no solvent field or dispersion terms included). The asymmetry induced at the non-classical bridging position was similar to that reported above for the ion-pair.
It might be of interest to repeat this study for the ion-pair rather than the cation, since the former is a more realistic model when comparing with what is actually found by experiment. It is also worth noting that including multiple explicit solvent molecules allows them to cross-polarize each other, thus probably increasing the interaction energies with the substrate. But on the other hand, I suspect that these interaction (free?) energies will be smaller for the ion-pair than for the cation alone.
Shown below is a plot of C-H….Oxygen (of water) non-bonded distances recorded in crystal structures. The C-H distance is “normalised” (to correct for over-shortening of CH bonds obtained from crystallography). The search was limited to H…O distances < 0.4Å shorter than the combined van der Waals radii.
There are clearly many examples in the region 2.2.-2.3Å, which correspond to the lengths computed above. Interestingly, the hot spot angle is ~160° rather than perhaps the expected 180°. There are quite a few outliers with distances down to about 1.7Å. It is probably worth investigating these for interesting effects. The scatter of points between 1.7 down to 1.2Å or at more acute angles are probably more likely to be crystallographic errors.
I also add here a more relaxed search, limited just to contacts at or below the van der Waals radius sum. As the interaction gets weaker, the angle departs more from 180°. The interactions appear to be a continuum, with no particular maximum at any distance.
Here is another crystallographic search (DOI: 10.14469/hpc/2437), this time for the solvation of chloride anion by water. The most probable H…Cl hydrogen bonded distance is ~2.2Å very similar to the results obtained in the model above.
I am occasionally adding further DFT methods and solvated models. Here is one calculated using the recent MN15 functional and this time using eight water molecules (DOI: 10.14469/hpc/2452) The two C-C lengths of the “non-classical” cation are 1.756 and 1.822Å, a difference of 0.066Å.
At which point one may well start to ask: “how much asymmetry is tolerated before one changes the definition from a non-classical bridged cation to a classical asymmetric one“? The [1,2] shifting normal mode however can still be clearly identified, and so the answer probably lies in the nature of that mode.
The main question of H.C. Brown was : what is the reason of the large exo-endo rate of 2-epimeric 2-norbornylesters in solvolysis? That is not the question to look at the nature of the persistent, stable 2-norbornyl cation.
For this system a Goering-Schewene Scheme has been deduced. But still Browns questions is not answered. It important, that the exo-endo ratio depends on the solvent: it is 350 in acetic acid, 850 in 60% ethanol water, and 1746 in hexafluoroisopropanol( with 3 % water). The later is a limiting solvent in solvolysis reactions.
It would be better to calculate the 2-norbornyl-cation in this solvent, not in water. The best would be to look for the TSs of the solvolysis of the epimeric esters in HFIP.
Dieter,
I can assure you that calculating the norbornyl cation chloride anion pair even in something as simple as water is absolutely non-trivial. Moving on to acetic acid or hexafluoroisopropanol is rather beyond the present computer resources. Never mind then moving on to transition states and more complex anions/leaving groups.
I am starting simple, and finding even that is complicated! But the point remains that the recent crystal structure was done in the crystal state with a non-coordinating/non-hydrogen bonding anion, and remains rather different from what goes on in hydrogen bonding solutions!
For what it is worth, I DID explore the TS for the solvolysis of tert-butyl chloride in water. That too was non-trivial (see here.)