Like benzene, its fully saturated version cyclohexane represents an icon of organic chemistry. By 1890, the structure of planar benzene was pretty much understood, but organic chemistry was still struggling somewhat to fully embrace three rather than two dimensions. A grand-old-man of organic chemistry at the time, Adolf von Baeyer, believed that cyclohexane too was flat, and what he said went. So when a young upstart named Hermann Sachse suggested it was not flat, and furthermore could exist in two forms, which we now call chair and boat, no-one believed him. His was a trigonometric proof, deriving from the tetrahedral angle of 109.47 at carbon, and producing what he termed strainless rings.
Whilst the chair form of cyclohexane now delights all generations of chemistry students, the boat is rather more mysterious. Perhaps due to Sachse, it is still often referred to as a higher energy form of the chair (Barton, in the 1956 review that effectively won him the Nobel prize, clearly states that the boat is one of only two conformations free of angle strain, DOI: 10.1039/QR9561000044). Over the last 30 years or so, and especially with the advent of molecular modelling programs, the complexity of the conformations of cyclohexane has become realised. A nice recent illustration of that complexity is by Jonathan Goodman using commercial software. Here a slightly different take on that is presented.
The starting point is the flat Baeyer model for cyclohexane. Like benzene, it has D6h symmetry. When subjected to a full force constant analysis using a modern program (in this instance Gaussian 09), this geometry is revealed (DOI: 10042/to-3708) to have three negative force constants, which in simple terms means it has three distortions which will reduce its energy. The eigenvectors of these force constants are shown below, and each set of vectors acts to reduce the symmetry of the species. Such symmetry-reduction is a well known aspect of group theory, and its analysis in the Lie symmetry groups is used in many areas of physics and mathematics, but it is a less used in chemistry.
| 348i cm-1 (B2g) | 244i (E2u) | 244i (E2u) |
|---|---|---|
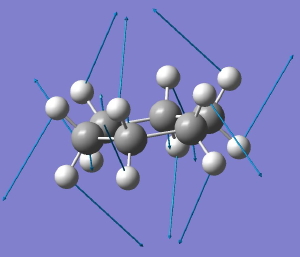 D6h to C2h for cyclohexane. Click for animation. |
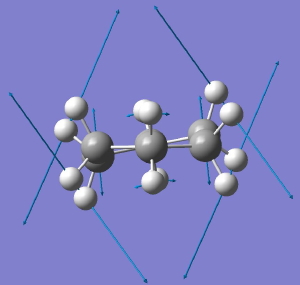 D6h to D2. Click for animation. |
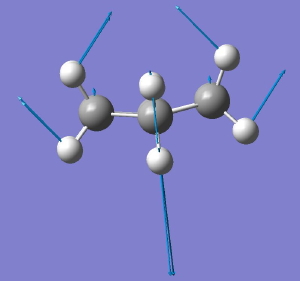 D6h to C2v. Click for animation. |
The first of these symmetry-reducing vibrations (the B2g mode) converts the geometry immediately to the chair conformation of cyclohexane. So in some ways, this use of symmetry is a modern equivalent of the trigonometry used by Sachse to prove his point.
The next two modes are degenerate in energy, and the first of these reduces the symmetry to D2. The result is what we now call the twist-boat. It is interesting, because the D2 group is one of the (relatively few) chiral groups, and the twist-boat exhibits disymmetric symmetry. In other words, following the vibrational eigenvectors in one direction leads to one enantiomer of the twist boat, and in the other direction to the other enantiomer. So (in theory only), one might actually be able to produce chiral cyclohexane (the experiment and resolution would have to be done at very low temperatures!). It is also interesting that theory nowadays could quite reliably calculate the optical rotation of this species (and its circular dichroism spectrum), so we certainly would know what to look out for.
The second component of the degenerate E imaginary mode leads directly to a species of C2v symmetry, which we recognize as Sachse’s second possible form of cyclohexane. The symmetry-reductions of D6h to C2h, D2 and C2v all have paths on the grand diagram of the 32 crystallographic point groups and their sub groups, and is an interesting application of group theory to a mainstream topic in organic chemistry.
But the story is not quite complete yet. The C2v boat is not the final outcome of the last distortion! It too is a transition state, connecting again the two D2 forms. So the path from D6h to C2v is NOT a minimum energy reaction path, but a rather different type of path known as a valley-ridge inflection path. An example of such a surface can be seen for the dimerisation of cyclopentadiene (DOI: 10.1021/ja016622h) and effectively it connects one transition state to a second transition state, without involving any intermediates on the pathway. At some stage, the dynamics of the system takes over, and the symmetry breaks without the system ever actually reaching the second transition structure. This final aspect of the potential energy surface of cyclohexane was not discussed by Jonathan Goodman in his own article on the topic.
So symmetry-breaking is the topic of this blog, and its connection to physics and mathematics. And, I might add that the same approach can be taken for looking at the conformations of cyclobutane, pentane, heptane and octane. But that will be left for another post.
Postscript. See this more recent post.
Tags: Adolf von Baeyer, animation, C, chair, conformational analysis, energy, General, Hermann Sachse, higher energy form, Interesting chemistry, Jonathan Goodman, minimum energy reaction path, model for cyclohexane, potential energy surface, symmetry breaking, Tutorial material
A thought-provoking post. I’m trying to get my head around how one might prepare the enantiomers of the twist-boat conformer mentioned. Heteroepitaxy on a chiral substrate? Magic?
There seems to be a dearth of discussion of symmetry breaking within the context of chemical structure. An interesting paper by Applegate, Barckholtz and Miller (DOI: 10.1039/a910269h) on Jahn-Teller distortions of cyclopenadienyl radical depicts a PES gratifyingly akin to the ‘Mexican Hat Function’ and how it gives rise to fluxional ‘pseudo-rotary’ sequences of equienergetic allylic and dienic structures. This post reminded me of that.
re the question about how to prepare enantiomers of twis-boat cyclohexane, I think magic is probably the best bet. But the twist-boat is normally prepared by rapid quench of high temperature cyclohexane on a super-cold surface. If that surface was itself chiral, one might at least be able to detect spectroscopically two distinct twist-boat sets of signals.
I will in fact calculate both [α]D and the OCD spectrum of the twist boat, to see exactly how large the optical properties are.
Whoops, that should be the cp radical C5H5.
I look forward to the rotation and dichroism results.
As promised, here are the calculated chiro-optical properties of D2-symmetric cyclohexane.
The [α]D is +38° (for the absolute configuration corresponding to this rotation, see DOI: 10042/to-3719), calculated for a chloroform solution at the frequency dependent value of 589nm (B3LYP/6-311G(d,p) level using Gaussian 09).
The circular dichroism (for the same absolute configuration) using time-dependent DFT is archived at 10042/to-3720 and is feature-full (I cannot post a graphic here in the comments), with positive phased peaks at 152, 142 and 133nm, and a negative phase peak at 128nm. The Cotton effect is also large (Δε ~200). (I rather doubt that commercial CD spectrometers can go so far into the UV however).
Whilst it is very unlikely that either value could be verified experimentally, it is interesting that the optical rotation is as high as it is!
That repository software is very cool and thanks for making the logfiles available – being able to open the structure in Avogadro really helps with visualising the species’ helicity.
Not being very familiar with the theory that gives rise to the magnitude of optical rotation, I take it that you would have expected a smaller rotation for a species lacking a stereogenic center and not being *massively* distorted from the C2h point group?
I know a spectroscopist who does a bit of CD (well, protein MCD) who I imagine may find this quite interesting.
re: repository. Thanks for noticing. We are the only group in computational chemistry who does this to my knowledge (although I did hear that the comp chem group at Erlangen has an archive of perhaps 300,000 calculations. Sadly however, its private). So it is nice to hear that you found it useful! That was indeed the intention.
re: Magnitude. Its really related to the hyperpolarisability rather than havng a stereogenic centre. Thus the “lemniscular” form of [14] annulene, that also has no stereogenic centre, has a rotation of around 3500 degrees. I have seen systems with no stereogenic centres with rotations > 100,000 degrees (sic).
Its the hyperpolarizability that does it, and π-electrons are particularly polarizable. Thus any system with (di)symmetric π electrons is going to have large rotations. It is also fair to say that such systems also have enormously variable optical dispersivity, ie frequency dependence. Thus some systems with rotations > 20,000 can go from -20,000, thru zero, to + 20,000 over 400 nm or so.
Is there a missing 1 in the DOI link to the Cp dimerisation?
what are the different methods used to measure the energy difference of substituted cyclohexanes?
In answer to the previous post, if you resolve the DOI for the calculation, it will take you to a repository where you can check any details of the calculation. In this case, it was done at the DFT level, B3LYP/6-31G(d). Of course, this was not intended to provide energies at the state-of-the-art level.
[…] an earlier post, I re-visited the conformational analysis of cyclohexane by looking at the vibrations of the […]
[…] any distance less than ~2.1Å now represents a genuine repulsion between the hydrogens (see also this post). This represents a somewhat more quantitative judgement on what used to be called steric […]
I really enjoyed reading this write-up and have recently been checking out your web site for some months now. I manage a website devoted to the fight against OCD (obsessive compulsive disorder) and would like to include your webblog within my information section for the advantage of my readers. There is certainly a great deal of falsehoods these days on the internet and anytime I happen across a very good high quality web-site similar to this I like to distribute these onto my readership — I am hoping this is alright with you, I’ve inserted your hyperlink within my highly valued resources section (on this page; http://www.whatisocd.org/resources/). Thank you – be sure to keep up the quality work it is very much valued.
Working on the give topic is really a difficult task but your this tutorial made it easy for me to handle it without any problem. If anyone seeking information then this blog is the best place for him as it has quality content for your required information. Thanks for sharing.
best baby swing
[…] to this mathematician (the interesting symmetrical and conformational properties of the central cyclohexane-like ring were still to be fully recognised by […]
[…] conformational analysis of cyclohexane is a mainstay of organic chemistry. Is there anything new that can be said about it? Let us start […]
Sir, How can I convert chair cyclohexane to boat cyclohexane by changing the dihedral angle? Which dihedral angle is to be considered?
The reaction coordinate for chair-chair or chair-twist boat conversions are complex, and cannot be represented by a single dihedral angle.
About 20 years ago, a coordinate was devised to accomplish this process, and if I track it down I will post it here.