The conformational analysis of cyclohexane is a mainstay of organic chemistry. Is there anything new that can be said about it? Let us start with the diagram below:
This identifies the start of the process as a chair conformation of cyclohexane, with D3d symmetry. I have highlighted a pair of hydrogens attached to the left most carbon atom in blue (equatorial) and magenta (axial). On the right hand side of the diagram this pair has transposed position, with the blue now being axial and the magenta equatorial. The same is true of the other five pairs of methylene hydrogens. We need to identify the pathway by which this happens. The pathway shown above proceeds through a half-chair transition state of C2 symmetry, falling to the first intermediate twist-boat of D2 symmetry before reaching a second transition state of C2v symmetry known as the boat. The whole diagram is mirror-symmetric about this point. The point to note about this diagram is that the species labelled C2 and D2 are dissymetric (chiral), whereas the ones labelled D3d and C2v are not. This means that there are two enantiomeric half-chair transition states, as there are the two twist-boats. This introduction of (di)symmetry does rather change the way we look at the process!
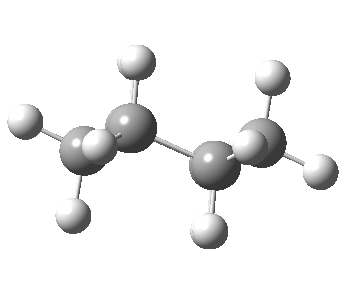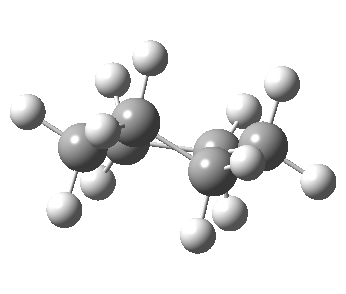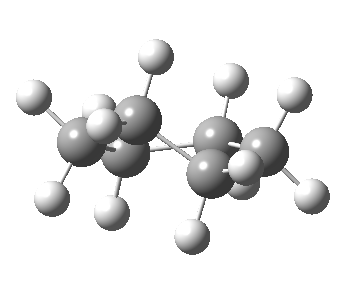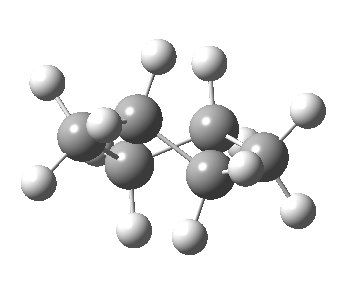
Now let me introduce the intrinsic reaction coordinate (IRC, ωB97XD/6-311G(d,p)/SCRF=cyclohexane), as followed from the half-chair transition state, and connecting the chair and the twist-boat.
| View 1 (click to see Chair ) | View 2 (click to see Twist-boat) |
 |
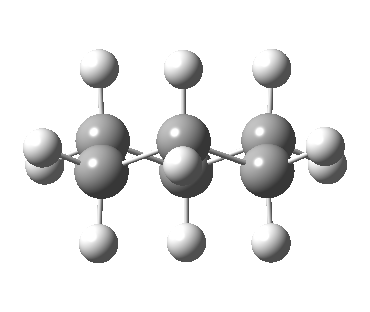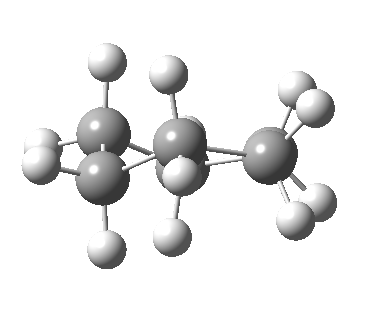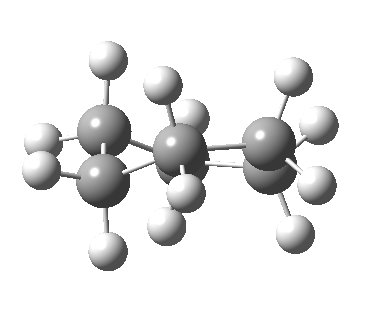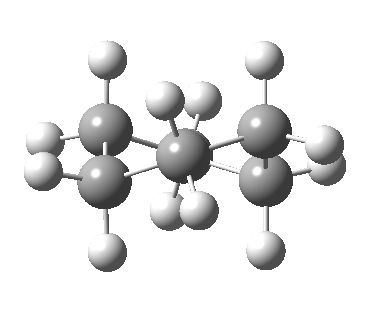 |
View 1 is looking down the C2 axis present in the half-chair transition state and both start and end points. View 2 rotates this by 90° along the y-axis, and is again looking down a C2 axis. This axis is present only when the IRC starts at the D3d chair conformation or reaches a D2 twist-boat conformation (becoming one of three at this point). The latter conformation is ~6 kcal/mol higher in energy than the chair. At this twist-boat geometry (shown below), the two hydrogens labelled with blue and magenta appear to be in an identical environment (in other words the axial or equatorial distinction between them is lost at this point). This might appear to be what we need to “flip” the environments of any pair of axial and equatorial hydrogens. But is it sufficient?
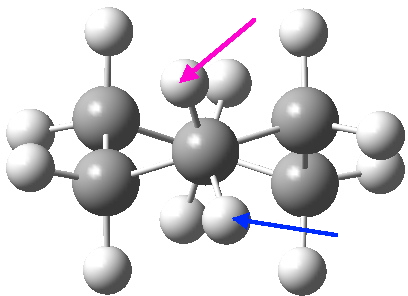
At the twist boat above, whilst the chemical environment of the pair of hydrogens identified with blue and magenta arrows is identical, their (pro)chirality is not. Because they both sit in a chiral molecule, their individual relationship to that chirality is said to be pro-chiral. The path shown above, on its own, does not interconvert the (pro)chirality of this pair of hydrogens. To do this, we need to get to the enantiomeric twist-boat conformation shown below, and this is achieved by passing through an achiral transition state of C2v symmetry, in other words a pure boat (see below).
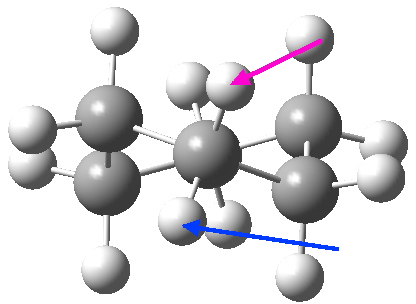
Well, now I pose a question. Is the above route the ONLY way of transposing the axial/equatorial identity of pairs of methylene hydrogens in this molecule? If you check the text books, some will in fact show a different diagram, in which the C2v boat is entirely uninvolved and only one enantiomer of the D2 twist-boat conformations is shown, as below.
These two pathways do differ fundamentally. The first (longer) pathway passes through an achiral boat transition state. The second (shorter) one involves two chiral half-chair transition states connecting a single chiral twist-boat, but implies that there must be two such pathways, each the enantiomer of the other. I should point out that since these two options share a common transition state, their energies are identical. Which one is the more realistic? I think only the technique of molecular dynamics, in which the momentum of the trajectories along the path is factored in, will tell us.
Postscript: The IRC for the enantiomerization of one twist boat into the other via a boat transition state is shown below. The axial-equatorial transpositions can be clearly seen in this view.
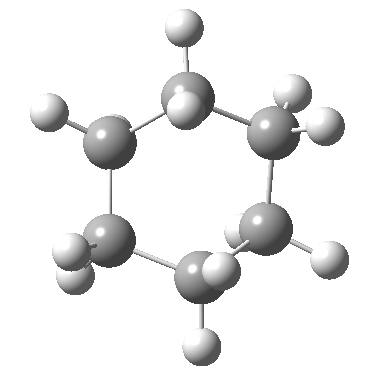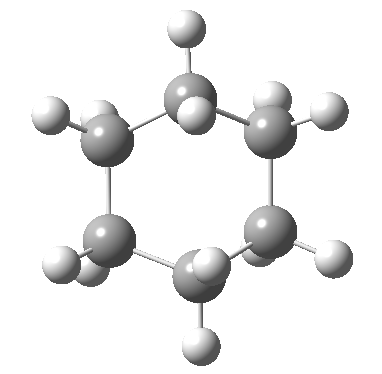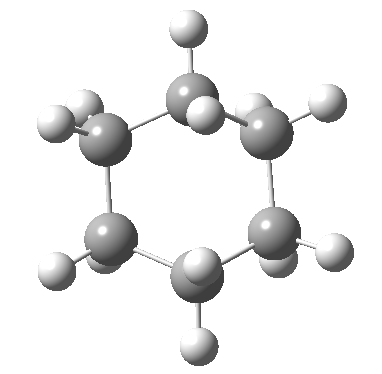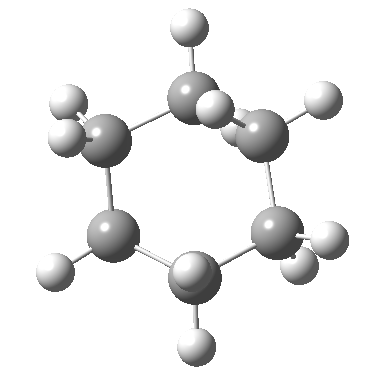
Tags: chair, chemical environment, conformational analysis, energy, Tutorial material
[…] Postscript. See this more recent post. […]
Still more elaborate depictions of the cyclohexane PES I have seen include the pseudororational interconversion of all the possible equivalent {“labelled”] C2v and D2 conformers and enantiomers in the center. Of course, there are many more C2 conformers are well.
Although it has 3 imaginary frequencies, planar D6h cyclohexane is of historical interest. since it was the geometry von Baeyer considered in his famous strain paper of 1884. Although refuted by Sachse (see Wilkipedia for wonderful details), Baeyer believed cyclohexane was planar to his dying day.
Since D3d (chair) cyclohexane is highly stabilized (about 17 kcal/mol) by six protobranches, it is should NOT be used as a model “strain-free” molecule.
One can indeed construct permutational maps connecting all possible half-chairs with paths to twist boats etc. It is indeed a complex hypersurface.
Hermann Sachse is indeed an interesting figure (I mentioned him and planar cyclohexane in an earlier blog). He used trigonometry to prove his theory, something that quite failed to get the message across to an audience of organic chemists.
Thank you so much sir, for the enlightening lecture. May I please ask you what is the driving factor that makes one twist-boat convert to boat conformer (first pathway) and exactly same another twist-boat to directly convert into half-chair conformer (second pathway); in case there are two pathways co-existing? In short, who determines the ensuing pathway of a twist-boat conformer?