One frequently has to confront the question: will a hydrogen bond form between a suitable donor (lone pair or π) and an acceptor? One of the factors to be taken into consideration for hydrogen bonds which are part of a cycle is the ring size. Here I explore one way of quantifying the effect for the series below, n=1-5 (4-8 membered rings).
I will use the NBO approach. To remind, this reduces the wavefunction for a molecule to a set of localised orbitals, referred to as natural bond orbitals. The perturbation interaction energy E(2) between any (doubly occupied, i.e. donor) orbital and an (unoccupied) acceptor orbital establishes the strength of that interaction. For a hydrogen bond, this can be expressed as the NBO corresponding to the (in this case oxygen) lone pair (shown in orange and purple below) and the corresponding H-O σ* empty orbital (shown as red and blue below). E(2) is a function both of how close in energy this pair of orbitals is (the smaller the energy gap the better) and how well they overlap (the relevant overlap in this case is the positive one between purple and blue). This latter attribute is shown below for the series n=2,3,4,5 (n=1 does not form any discernible hydrogen bond), at the ωB97XD/6-311G(d,p) computational level.
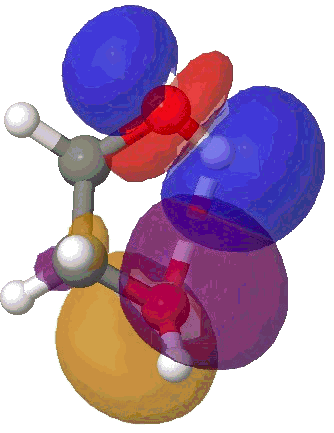 NBO interaction for 5-ring H-bond. |
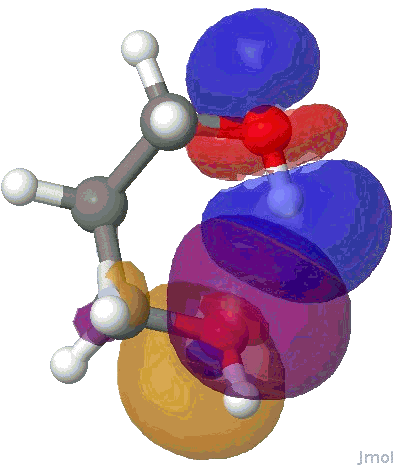 NBO interaction for 6-ring H-bond. |
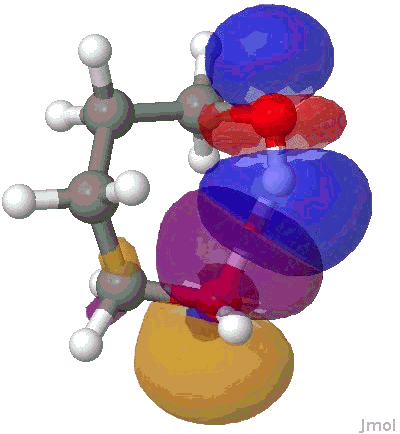 NBO interaction for 7-ring H-bond. |
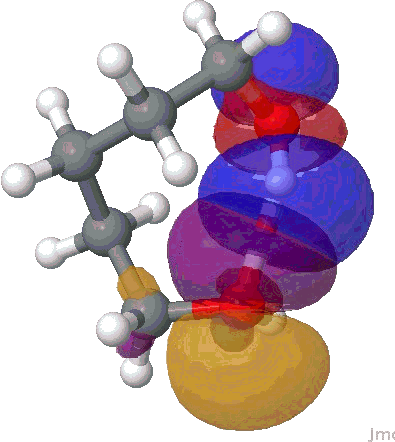 NBO interaction for 8-ring H-bond. |
The interaction energies E(2) are collected below, together with the computed lengths. To put E(2) into context, it is around 16 kcal/mol for a strong anomeric interaction, and about 6 kcal/mol for the stereoelectronic influence in di-fluoroethane. One can see that by the time the angle subtended at the hydrogen has increased to ~150°, the interaction energy has reached a respectable value.
| n | E(2), kcal/mol | O…H length, Å | Angle, ° |
|---|---|---|---|
| 1 | ~0.0 | – | 81.8 |
| 2 | 0.75 | 2.294 | 109.7 |
| 3 | 3.56 | 1.984 | 139.6 |
| 4 | 6.24 | 2.017 | 146.5 |
| 5 | 8.35 | 1.957 | 153.4 |
So the simple trick of looking at the donor-acceptor NBO interaction in a cyclic hydrogen bond can give us a straightforward way of quantifying how the size of the ring and hence the orbital overlap (one presumes that the Lp/C-O σ* energy gap is similar for all the systems) affects the strength of the interaction. One might also explore this by looking at structures in the Cambridge crystal database. But note from the above that whilst the E(2) energies follow ring size, this does not appear to happen for the H…O lengths! The analysis reveals that the maximum number of structures for the span 5 to 8-rings occurs at ~2.15, 1.85, 1.65 and 1.85Å respectively.
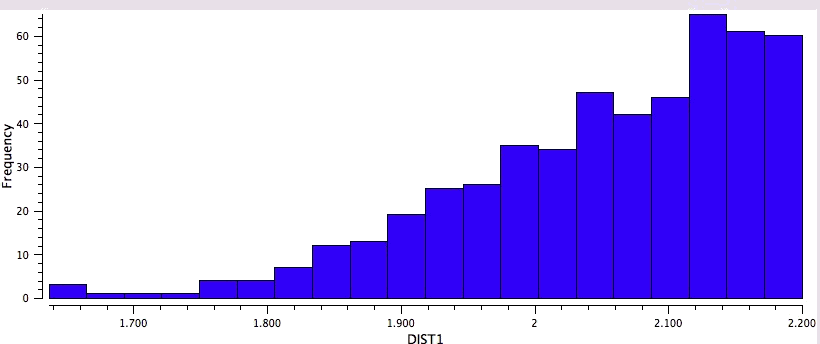 Crystal data for 5-rings |
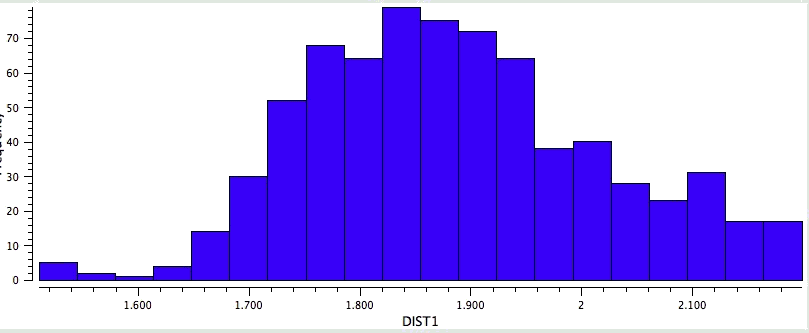 Crystal data for 6-rings. |
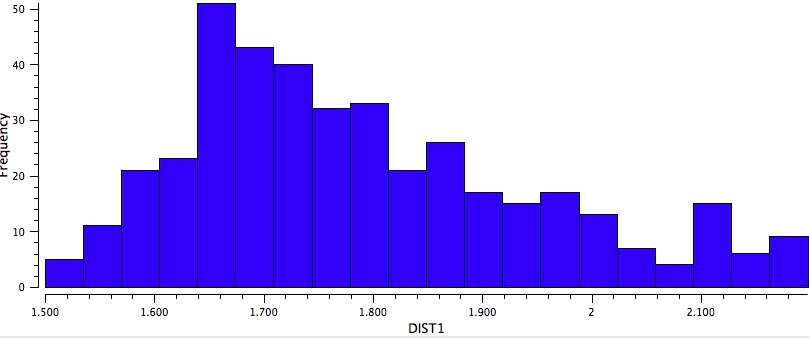 Crystal data for 7-rings |
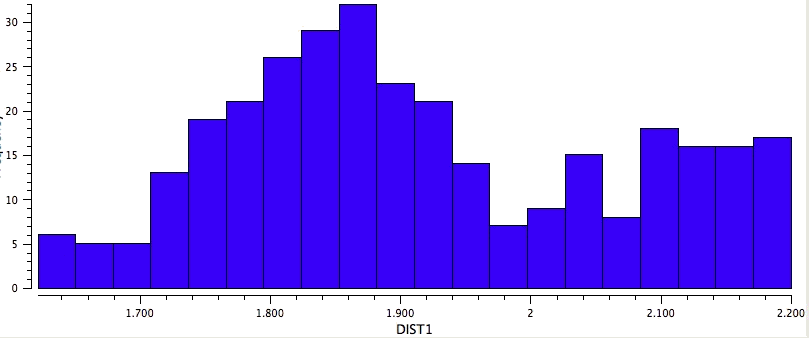 Crystal data for 8-rings |
Tags: Cambridge, energy, energy gap, interaction energy, Tutorial material
[…] correlation between a ring size and the hydrogen bonding O(Lp) H-O σ* interaction in that ring indicated a 7- or 8-membered ring was preferred over smaller ones. Here is the same study, but this time […]
[…] 2 is a more conventional OH…O bond, but as part of a 5-membered ring. As we saw before, these types of hydrogen bond are quite weak, and you can see this reflected in the blue attractive […]