Henry Rzepa's Blog

Henry Armstrong studied at the Royal College of Chemistry from 1865-7 and spent his subsequent career as an organic chemist at the Central College of the Imperial college of Science and technology until he retired in 1912. He spent the rest of his long life railing against the state of modern chemistry, saving much of his vitriol against (inter alia) the absurdity of ions, electronic theory in chemistry, quantum mechanics and nuclear bombardment in physics. He snarled at Robinson’s and Ingold’s new invention (ca 1926-1930) of electronic arrow pushing with the put down “bent arrows never hit their marks“.^‡  He was dismissed as an “old fogy, stuck in a time warp about 1894.”^‡ So why on earth would I want to write about him? Read on…

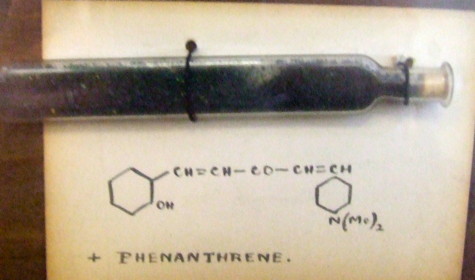
He did worthy (nowadays this could mean dull) chemistry on e.g. naphthalenes, but I want to focus on two articles from the period 1887-1890[cite]10.1039/CT8875100258[/cite],[cite]10.1039/PL8900600095[/cite]. Let me set the scene by reminding of an earlier post showing the structure of a bis(stilbyl)ketone, dated 1921. The two aromatic groups (yes, they really are such) are drawn in the manner we would nowadays draw cyclohexane. This practice in fact continued in texts and articles for perhaps 30 more years! Not much sign of electronic accounting there then! And by a professor at Imperial College no less, where Armstrong had been.

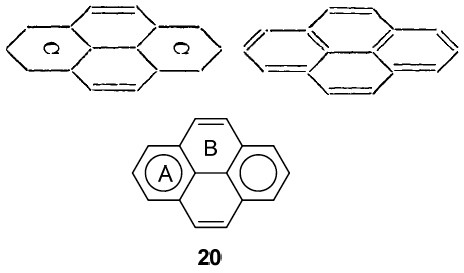
So when would you date the diagrams below? So called Clar^† representations, originating from the 1950s? The one on the bottom below cites Clar and dates from 2010[cite]10.3390/sym2031653[/cite], but the one above it comes from Armstrong’s 1890 article!

Clar representations are used to count electrons (as coming in six packs). But there is little doubt that Armstrong’s use of a “C” (or inner circle, which is exactly what it is) means six as well. The evidence I present below, taken from his 1887 article.

1. He counts the six carbons as having a total of 24 what he calls affinities (definition: An attraction or force between particles that causes them to combine), or four per carbon. Let us make life easy and equate affinity=electron (remember, the electron itself was not yet discovered or named!). He disposes of 12 affinities/electrons to form what we now call six carbon-carbon σ bonds, and a further six for the  six C-H bonds.
2. He is left with exactly six affinities/electrons, which he presupposes to act upon each other, in the manner of resultants (the old term for vectors). In fact, he replaces these six vectors by a circle (the inner circle) in his second article of 1890.
3. He invents delocalization in all but name when he states that any one atom has an influence on other atoms not contiguous to it in the ring (he really did have o/m/p directing influence in mind here).
4. He compares the introduction of a substituent (R, which comes from the old name Radicle) perturbing the distribution of the affinity to how electric charges perturb each other. So, the affinity behaves as if it might have electrical (from which the name electron came of course) properties? And it might be described by a vector?
5. Remember, this is a scientist who in later life did not believe in electronic theories of chemistry? Really? Well, again in 1890:

6. Here, he is refining his vector representation of affinities, saying that these vectors in effect define a circle, an inner circle no less. One that can be disrupted  (Robinson some 30 years later wrote[cite]10.1039/CT925270160[/cite] of how the cycle of six electrons are able to form a group that resists disruption) when an additive compound is formed (his examples are all electrophiles, what we now call electrophilic addition) such that the remaining carbons become merely unsaturated. There seems little doubt he is describing what we now call a Wheland Intermediate.
7. Is this really a man who did not believe in electronic theories of chemistry? What about that concluding paragraph then? The laws of substitution require a knowledge of the inner structure of (what we now call the aromatic) hydrocarbons?
8. And that such speculations may suggest fresh lines of experimental inquiry? This all sounds very much like the modern use of quantum mechanics and its electronic eigenvectors to describe the probability distribution of electrons (remember, Armstrong did not approve of this either) to probe the inner structure of molecules and to suggest new experiments.

We have a real mystery. Armstrong got so very close to a modern theory of chemistry. Was he asleep when Stoney named the electron around 1891 and Thomson discovered it in 1897? If only he had followed his own advice! Ah well, just as well he was ignored in the 20th century when he preached against it all.

---

^‡W. H. Brock, “The case of the Poisonous Socks”, chapter 20, RSC Publishing, 2011, 978-1-84973-324-3 ^†Clar, E. The Aromatic Sextet; Wiley: New York, NY, USA, 1972.

---

Tags: Central College, electronic accounting, Henry Armstrong, Historical, Imperial College, Imperial college of Science and technology, New York, organic chemist, professor, Royal College of Chemistry, RSC Publishing, scientist, Stoney, Thomson, United States

This entry was posted on Monday, November 7th, 2011 at 9:58 pm and is filed under Historical. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.