In a recent post, I told the story of how in the early 1960s, Robert Woodward had encountered an unexpected stereochemical outcome to the reaction of a hexatriene, part of his grand synthesis of vitamin B12. He had constructed a model of the reaction he wanted to undertake, perhaps with the help of a physical model, concluding that the most favourable of the two he had built was not matched by the actual outcome of the reaction. He was thus driven to systematise such (Pericyclic) reactions by developing rules for them with Roald Hoffmann. This involved a classification scheme of “allowed” and “forbidden” pericyclic reactions and his original favoured model in fact corresponded to the latter type. When physical model building in the 1960s was gradually replaced by models based on quantum mechanical calculations from the 1970s onwards, the term “allowed” morphed into “a relatively low energy transition state for the reaction can be located” and very often “no transition state exists for a forbidden reaction”. The famous quote “there are no exceptions” (to this rule) was often interpreted that if a “forbidden reaction” did apparently proceed, its mechanism was NOT that of a pericyclic reaction. Inspired by all of this, I recollected a famous “exception” to the rules which is often explained by such non-pericyclic character, the Stevens rearrangement[1],[2],[3] by a 1,2-shift.
Here, R = benzyl (in the original experiment). The crucial point here is that the reaction readily proceeds at moderate temperatures and that if the R group is chiral, it proceeds with retention of configuration. Why was this remarkable? Because if this is indeed a four electron 1,2-sigmatropic pericyclic reaction, it is predicted to proceed with inversion of configuration at the R group. So 1,2-migration with retention would be an exception to the Woodward-Hoffmann rules and to avoid being an exception, it clearly cannot be a pericyclic reaction! Time for some calculations, at the B3LYP+GD3BJ/Def2-SVP/SCRF=water level (FAIR Data DOI: 10.14469/hpc/7855)
The above is the classic 1,2-sigmatropic migration of a benzyl group from N to C, proceeding with retention of configuration. Hey, look at the barrier (TS1, ΔG‡ 48.2 kcal/mol), which is way too high to be a viable reaction. This teaches us the first lesson; it can be possible to locate the transition state for “forbidden” thermal reactions, but it is likely they will be very high in energy. Forbidden in this case means in terms of energy; sometimes it can mean in terms of orbital symmetry, or even transition state anti-aromaticity.
Now we have to do something clever with the keywords for the calculation. This involves adding guess(mix.always) and running a spin unrestricted version, ub3lyp. This does a very simple CI (configuration interaction), mixing the HOMO and LUMO to allow an open-shell biradical as a solution for the wavefunction. In effect we are mixing an excited state into the wavefunction, which reflects the Woodward-Hoffmann observation that a “forbidden” thermal reaction can proceed as an “allowed” photochemical, i.e. excited state, reaction! Now one gets an entirely different outcome, with an activation free energy of TS2, ΔG‡ 13.9 kcal/mol, a facile thermal reaction.
At IRC values of -4 to zero, simple C-N bond cleavage occurs. The closed shell reactant has a value for the spin expectation operator <S**2>= 0.0000, but by the TS, it has acquired the value <S**2>= 0.4214. To give you an idea of what this means, a “pure” biradical has a value of <S**2>= 1.0000. So this is half way to becoming a pure biradical, and in effect also half way from a pure closed shell ion-pair (which would again have <S**2>= 0.00000). From IRC = +1 to IRC = +10, this continues to evolve, reaching a maximum value of <S**2>= 1.0084 at ~IRC 11 (a pure biradical). Then the value of <S**2> collapses rapidly to 0.000, indicating formation of an ion pair, but only well after the transition state is passed. This ion pair then recombines to form a C-C bond and the final product.
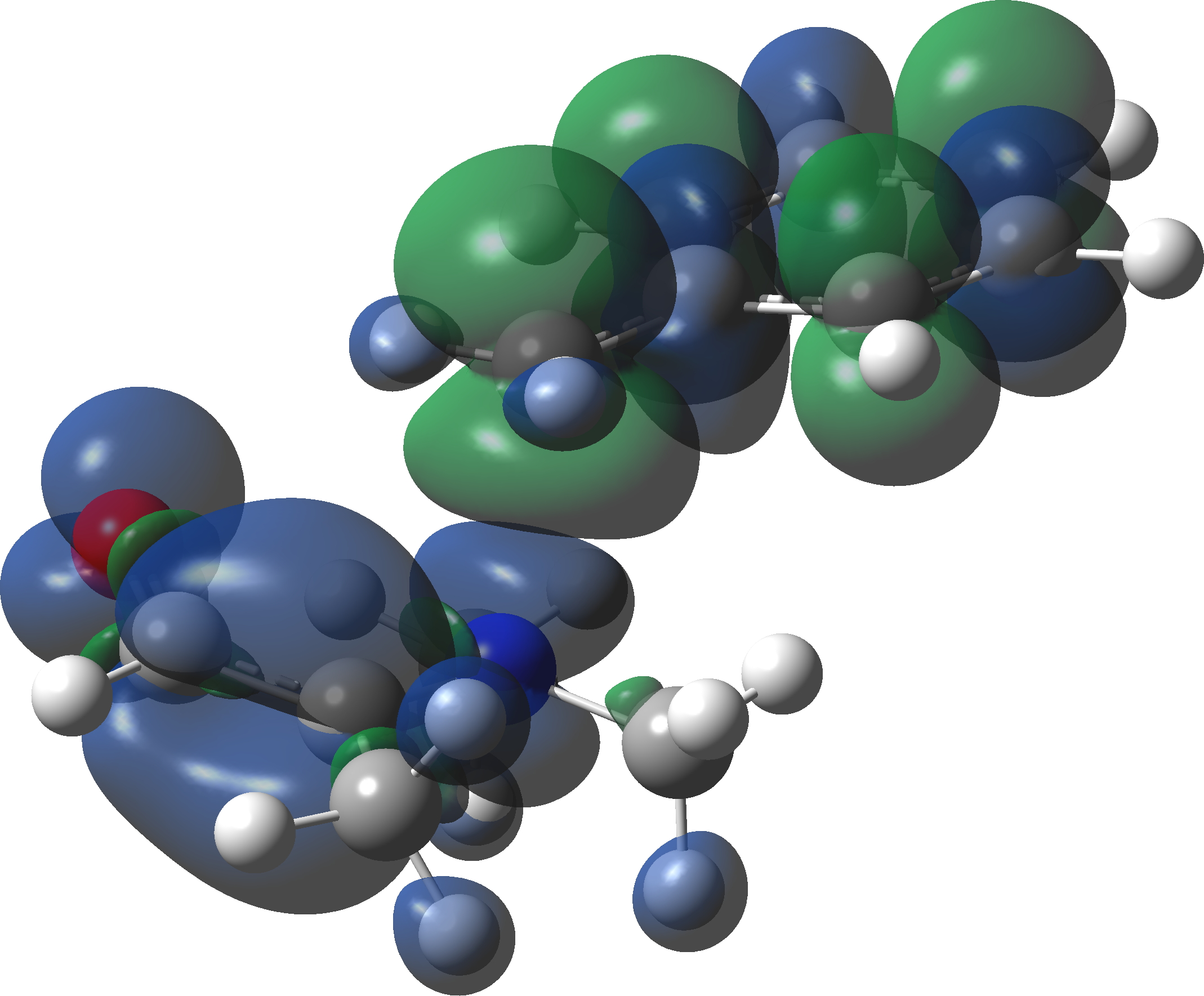
Spin density at TS2. Click to view 3D model
So to summarise, the Stevens 1,2-rearrangement is a very asymmetrical process, breaking the C-N bond long before the C-C bond starts to form. In this sense it is really not a pericyclic reaction! At the transition state, it has character of both a biradical and an ion-pair, very much a Janus-like mechanism with two faces to it.
But what of the stereochemistry? Well, here is a suggestion. As it progresses on its way, first to acquire biradical character and then to lose that in favour of ion-pair character, the phenyl group retains its involvement with the rest of the molecule via dispersion attractions. So these dispersion terms may well be strong enough to prevent the phenyl group from any rotations that would be required to produce stereochemical inversion rather than the observed retention. I do not believe that the role of dispersion attractions in the Stevens mechanism has been proposed before. A colleague who works with fluorinated compounds has suggested that perhaps fluorinated substrates may show different dispersion behaviours, maybe leading to stereochemical scrambling. An experiment worth doing?
References
- T.S. Stevens, E.M. Creighton, A.B. Gordon, and M. MacNicol, "CCCCXXIII.—Degradation of quaternary ammonium salts. Part I", J. Chem. Soc., vol. 0, pp. 3193-3197, 1928. https://doi.org/10.1039/jr9280003193
- T.S. Stevens, "CCLXX.—Degradation of quaternary ammonium salts. Part II", J. Chem. Soc., vol. 0, pp. 2107-2119, 1930. https://doi.org/10.1039/jr9300002107
- T.S. Stevens, W.W. Snedden, E.T. Stiller, and T. Thomson, "CCLXXI.—Degradation of quaternary ammonium salts. Part III", J. Chem. Soc., vol. 0, pp. 2119-2125, 1930. https://doi.org/10.1039/jr9300002119