In an earlier post, I pondered on how the “arrow pushing” for the thermal pericyclic reactions of some annulenes (cyclic conjugated hydrocarbons) could be represented in terms of either two separate electrocyclic reactions or of one cycloaddition reaction. Each reaction is governed by selection rules which can be stated in terms of the anticipated aromaticity of the pericyclic transition state as belonging to a 4n or a 4n+2 class. This in turn determines whether the topology of the transition state belongs to a class of aromatic species known as either Hückel or Möbius. Here I play with the observation that by adding or removing two electrons from the molecule, the two classes 4n and 4n+2 can be swapped. What happens to the aromaticities of the transition states if that is done?
The test bed is a [20]annulene, which might undertake either a eight electron (4n) 4s+4s cycloaddition in the inner ring, or two eight electron (4n) electrocyclic reactions in the outer rings in which the new bond is formed antarafacially from opposite faces. The selection rules suggest that the former must proceed through an anti or non-aromatic Hückel transition state and the latter through an aromatic Möbius transition state.
We are measuring the aromaticity by using the so-called NICS NMR method, for which an aromatic value is a negative chemical shift for the NICS probe, a non-aromatic value is ~0 and an anti-aromatic value a positive chemical shift. The location of these probes is determined by analysis of the critical points in the electron density of the transition states and placement at either the ring or the cage critical point so determined.
| # | System | Charge | ν(s) | ν(a) | NICS (outer rings) | NICS (inner ring) | ΔG | DOI |
|---|---|---|---|---|---|---|---|---|
| 1 | trans, D2 | 0 | -399 | -433 | -6.7 | -0.3 | -774.036424 | 7483 |
| 2 | trans, D2 | +2 | -388 | -399 | +4.0 | +2.1 | -773.381567 | 7490 |
| 3 | trans, D2 | -2 | -412 | -324 | -15.0 | -12.9 | -774.179873 | 7526 |
| 4 | cis, Cs | 0 | -413 | -369 | -8.6 | -5.4 | -774.048172 | 7482 |
| 5 | cis, Cs | +2 | -640 | -453 | +11.1 | +2.1 | -773.386424 | 7493 |
| 6 | cis, C2 | 0 | -491 | -459 | -8.3 | +1.4 | -774.059141 | 7486 |
| 7 | cis, C2 | +2 | -685 | -479 | +10.5 | +2.3/+3.7 | -773.392100 | 7497 |
| 8 | cis, C2 | -2 | -926 | -533 | +8.4 | -13.9 | -774.2029900 | 7525 |
Each of the stationary points located is in fact a saddle point of order 2 (and in some cases 3), with ν(s) corresponding to normal vibrational mode for synchronous formation of both bonds, and ν(a) to formation of one C-C bond but cleavage of the other. The fact that both the force constants for these modes are negative suggests that the two electrocyclic reactions are independent and occur consecutively rather than concurrently. This then argues against it being a synchronous cycloaddition reaction, but could of course still be a highly asynchronous one.
The first three examples are in fact for a [20]annulene with a central trans rather than cis double bond (as illustrated above), resulting in D2 symmetry. The neutral system has the outer ring aromatic (-ve NICS) and the inner ring non-aromatic, as appropriate for the rules stated above. Removing two electrons might you would imagine swap these two, but of course the electrons are removed from the entire [20]annulene as a whole, and not from specific regions. In fact it results in mildly anti-aromatic rings in both regions. Adding two electrons now makes the rings strongly aromatic, behaving as if the two electrons have really only modified the inner cycloaddition reaction.
The reactions with a cis stereochemistry at the central bond again confirm for the rules for the neutral annulene, but now the dianion predicts the outer ring to be anti-aromatic and the inner one aromatic, with a reversal of aromaticity for both sets of rings. Despite the cycloaddition now being an aromatic transition state, the force constants still indicate it to be asynchronous. But the observation that ν(s) is now significantly larger than ν(a) suggests that perhaps the reaction can indeed now be considered as at least in part an asymmetric cycloaddition.
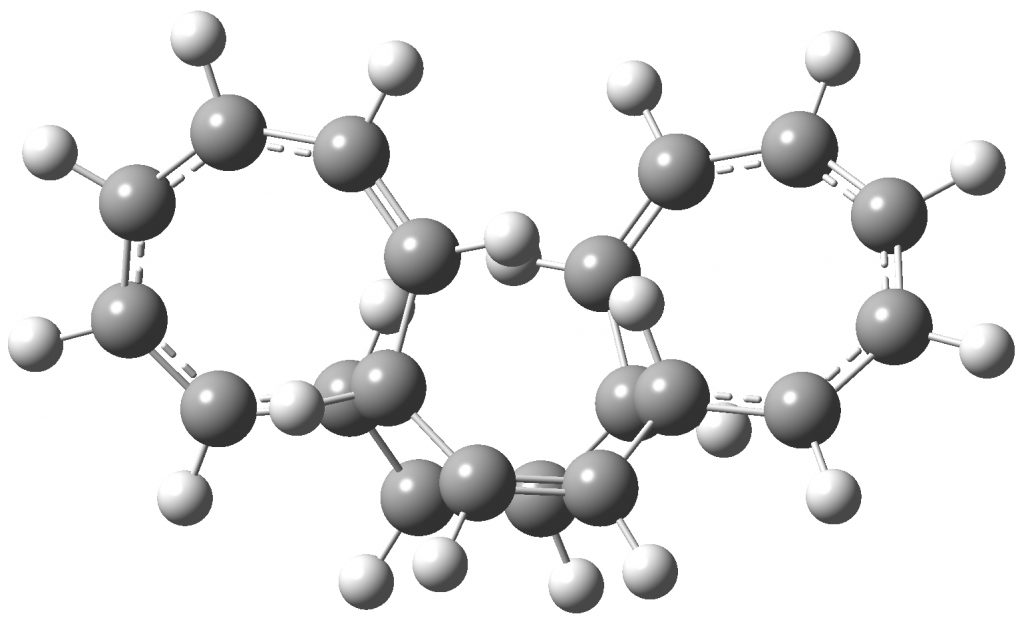
Click to view vibrational modes
What is the point of doing these calculations, you may well ask? Its unlikely that they could ever be subjected to experimental tests! Well, here we are using quantum mechanical calculations as an experimental procedure in its own right, to try to push the simple pericyclic selection rules beyond anything envisaged by its original formulators.