I occasionally spot an old blog that emerges, if only briefly, as “trending”. In this instance, only the second blog I ever wrote here, way back in 2009 as a follow up to this article.[1] With something of that age, its always worth revisiting to see if any aspect needs updating or expanding, given the uptick in interest. It related to the observation that there can be more than one way of expressing the “curly arrows” for some pericyclic reactions. These alternatives may each represent different types of such reactions, hence leading to a conundrum for students of how to label the mechanism. I had noted in that blog that I intended to revisit the topic and so a mere eleven years later here it is!
Annulenes, or cyclic conjugated polyenes can (hypothetically) indulge in transannular cyclisations which can be regarded as either two electrocyclic reactions, or one cycloaddition reaction, or perhaps a chimera of all three which here I describe as trimerous. Locating the transition states for such a trimerous reaction is quite straightforward and here I give the FAIR data DOI for all the examples shown below (DOI: 10.14469/hpc/7440).‡ The calculations are all at the B3LYP+GD3BJ/Def2-TZVPP level.
The central reaction can be represented as a cycloaddition in which two new bonds form between the termini of two conjugated alkenes. The stereochemistry for each alkene component is defined as either suprafacial (the two new bonds form to the same face of that alkene) or antarafacial (the two new bonds form on opposite faces of that alkene). Another way of representing the curly arrow mechanism is to draw to separate electrocyclic reactions, in which one new bond is formed between the termini of a conjugated alkene. If this bond connects at each end to the same face of that alkene, the bond forms suprafacially, if it connects opposite faces of that alkene it forms antarafacially. One must also count the number of cyclic curly arrows used in each representation; the examples above illustrate two, three or four curly arrows, representing four, six or eight electrons. One can now combine these attributes to form some selection rules.
For thermal reactions, one can state that if the total electron count represented by an odd number of curly arrows corresponding to the formula 4n+2 (n = 0,1,2, etc, the n is NOT the same as that shown in the scheme above) and there are either no (or an even number of) antarafacial components, the reaction will be “allowed” and proceed through a “Huckel aromatic transition state“. Alternatively, if the total electron count corresponds to an even number of curly arrows matching the formula 4n (n=1,2, etc) and there is one (or an odd number of) antarafacial components, the reaction will this time proceed through a “Mobius aromatic transition state“. These are in fact a concise alternative statement of the Woodward-Hoffmann selection rules for thermal pericyclic reactions.
| Entry # | n (scheme only) | [ ]-Annulene TS |
electron count in each ring |
s/a components |
NICS for each ring centroid |
|---|---|---|---|---|---|
| 1 | 0 | 10 endo | 4,6,4 | a,s+s,a | -3.5,-15.3,-3.5 |
| 2 | 0 | 10 exo | 4,6,4 | a,s+s,a | -2.8,-11.6,-2.8 |
| 3 | 0 | 12, saddle=1♠ | 4,8,4 | s,s+a,* | -0.1,-10.3,-2.0 |
| 4 | 0 | 12, saddle=2 | 4,8,4 | *,s+a,* | -0.9,-10.7,-0.9 |
| 5 | 1 | 14 endo | 6,6,6 | a,s+s,a | +2.2,-17.1,+2.2 |
| 6 | 1 | 14 exo | 6,6,6 | a,s+s,a | +9.7,-11.1,+9.7 |
| 7 | 1 | 16 | 6,8,6 | a,s+a,a | +9.1,-9.6,+9.1 |
| 8 | 2 | 18 endo, saddle=1 | 8,6,8 | s,s+s,a | -2.0,-15.0,-♥ |
| 9 | 2 | 18 endo, saddle=2 | 8,6,8 | *,s+s,* | -0.5,-17.1,-0.5 |
| 10 | 2 | 18 exo,saddle=1 | 8,6,8 | a,s+s,a | -6.2,-4.5,-3.7 |
| 11 | 2 | 18 exo,saddle=2 | 8,6,8 | a,s+s,a | -8.2,-1.4,-8.2 |
| 12 | 2 | 20,saddle=3 | 8,8,8 | a,s+*,a | -8.5,+0.3,-8.5 |
♥No ring centroid in AIM analysis.♠The symmetrical geometry has two negative force constants (saddle=2), representing an asymmetric distortion to a true transition state (saddle=1).
For the reactions shown in the scheme above, we will determine the NICS (Nucleus independent chemical shift) value at the ring centroid of each reaction to ascertain the aromaticity in that ring. The effective ring centroid in turn is located by performing an AIM analysis of the topology of the electron density and locating the RCP (ring critical points in that density; a critical point itself is one where the first derivatives of the density with respect to the three cartesian coordinates is zero) or in several examples the CCP (Cage critical point). I will discuss some of these systems individually, but in fact there is a wealth of information available for each one and to discover it all, you should go to the data files and inspect all the structures for yourself. Firstly, the colour code in the table above:
- In the s/a column, blue represents systems where the electrocyclic component forms a bond antarafacially. whereas the cycloaddition component forms both bonds suprafacially to both the alkene and the diene.
- Red represents systems where the electrocyclic component forms a terminus bond antarafacially and the cycloaddition component forms a bond suprafacially to the alkene but antarafacially to the diene.
- Where the π-system in the pericyclic transition state has a local orthogonality (i.e. the pericyclic π-system is locally twisted by 90°±6 at one point) it is not possible to confidently distinguish between supra and antarafacial. Such instances are declared non-aromatic and are shown in black.
- In the NICS column, green represents an aromatic value and red an antiaromatic value. Black is effectively non-aromatic.
Individual entries
The way to read the table above is the following. In the 4th column (electron count in each ring, corresponding to the curly arrows representing the reaction at that ring), determine if the count belongs to the 4n or the 4n+2 rule. Next for each ring, is the number of antarafacial components odd, or zero.† Finally, does the NICS aromaticity index match with the inference from the first two properties, i.e. 4n+2 + zero a = aromatic, 4n + odd a = aromatic and the corollary of 4n+2 + odd a = anti-aromatic, 4n + zero a = anti-aromatic.
Entry 1: All three rings correspond to aromatic pericyclic transition states, but with the cycloaddition ring far more aromatic than the electroclisation rings. This is reflected in the bond lengths in the rings. The cycloaddition ring has lengths close to the “aromatic” value of 1.4Å. whereas the electrocyclic rings have highly alternating bond lengths. The calculated lengths correspond to the “cycloaddition” curly arrows in the scheme above and not to the “electrocyclic” arrows. This reaction does not have the characteristics of three simultaneous pericyclic reactions, or to use the parlance of the title of this post, it is not trimerous.
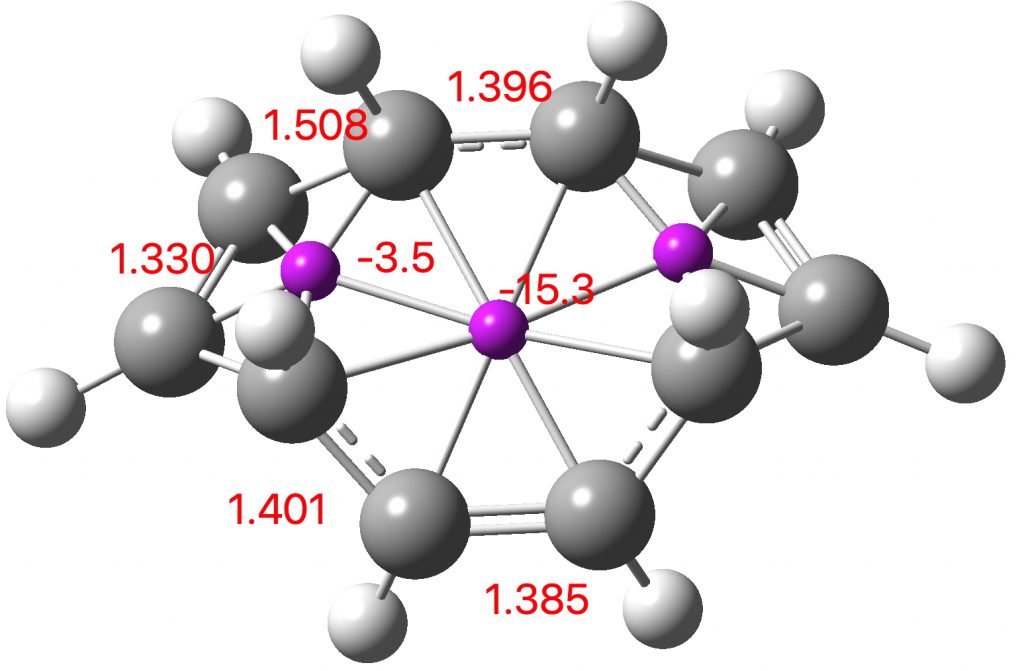
Click image to see 3D model.
Entry 6: This time, the central ring is again strongly aromatic (4n+2 + zero a = aromatic) but the two outer rings are strongly antiaromatic (4n+2 + odd a = anti-aromatic). Again the curly arrows correspond to cycloaddition and not electrocyclisation.
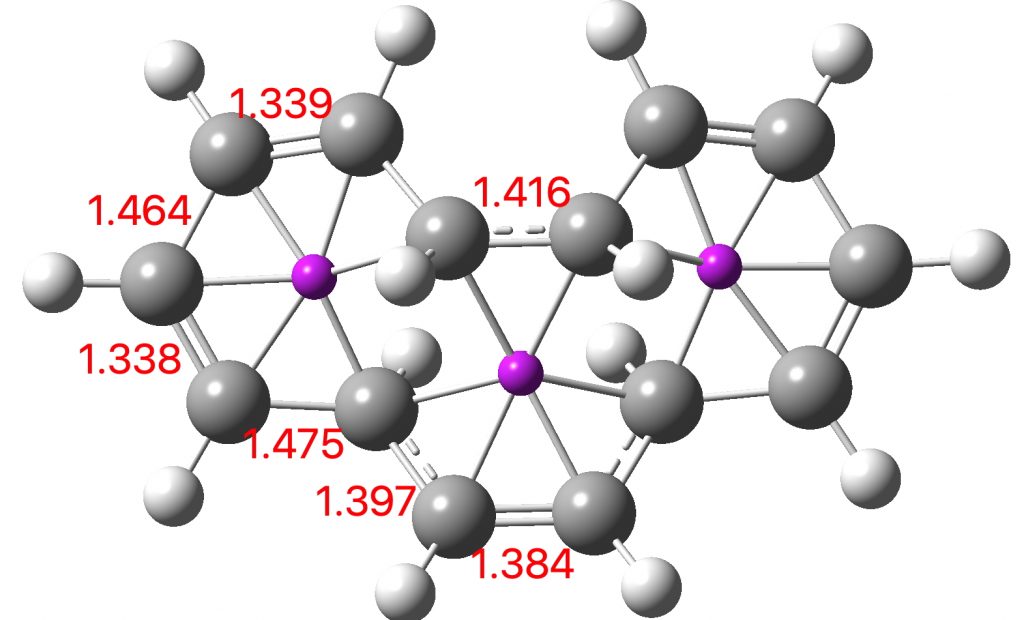
Click image to see 3D model.
Entry 11: As with entry 1, all three rings should again be aromatic (4n+2 + zero a = aromatic;4n + odd a = aromatic).In reality the bond lengths and aromaticity indicate that this time the curly arrows are those of two concurrent electrocyclic reactions and NOT of one cycloaddition. But there is a sting in the tail. This symmetrical system is NOT a true transition state.
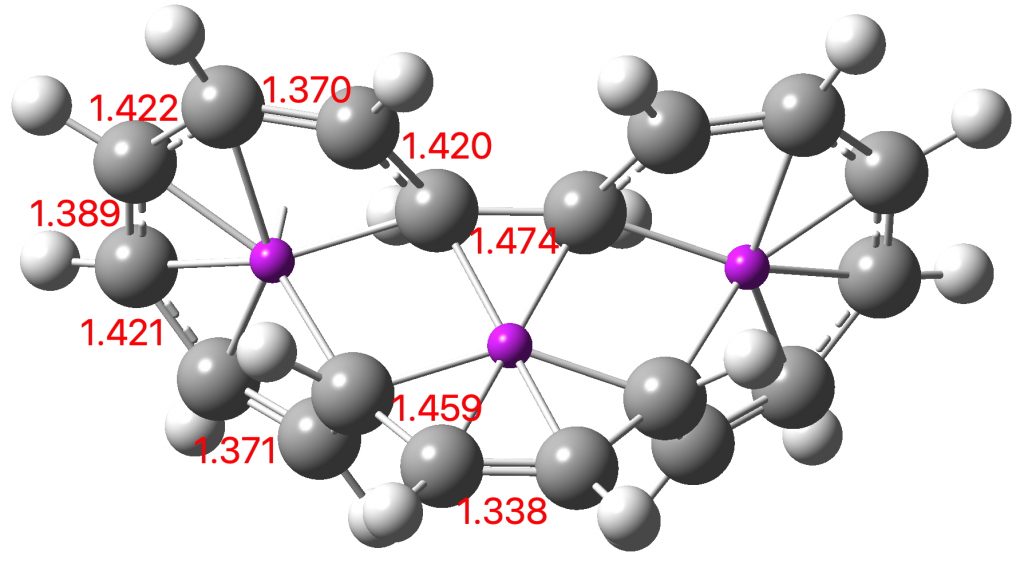
Click image to see 3D model.
Entry 10: This is the true transition state corresponding to entry 11, in which completion of one electrocyclic reaction preceeds the other; they are no longer synchronous but asynchronous, with one C-C bond (1.946Å) formed before the other (2.790Å). This pericyclic reaction can indeed be now considered trimerous, albeit with the three individual pericyclic reactions happening at different rates.
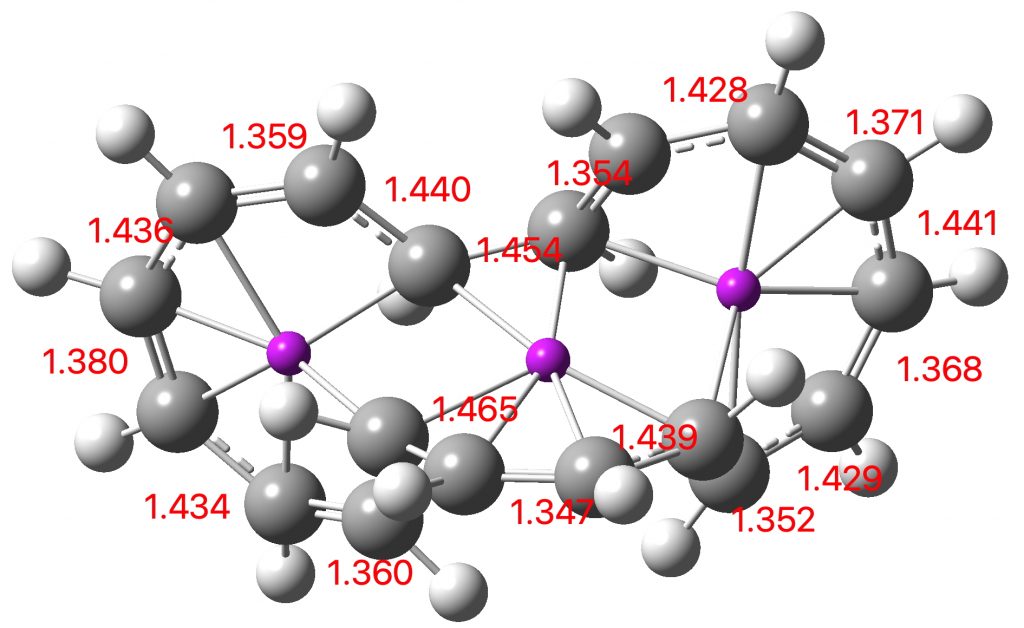
Click image to see 3D model
We can see that allowed pericyclic reactions in which three separate modes operate in concert (trimerous) are unlikely to happen. In effect the “aromaticity” tends to localise in one region rather than operate simultaneously in three rings. The collection of examples above also nicely illustrates the operation of the Woodward-Hoffmann rules as recast in terms of transition state aromaticity.
‡The original blog was also data rich, containing the encouragement to Click above to obtain model. It did not however cite the DOI of the repository entry for this data, an omission here rectified. †Or even, but no examples of this in the table.
References
- H.S. Rzepa, "The Aromaticity of Pericyclic Reaction Transition States", Journal of Chemical Education, vol. 84, pp. 1535, 2007. https://doi.org/10.1021/ed084p1535