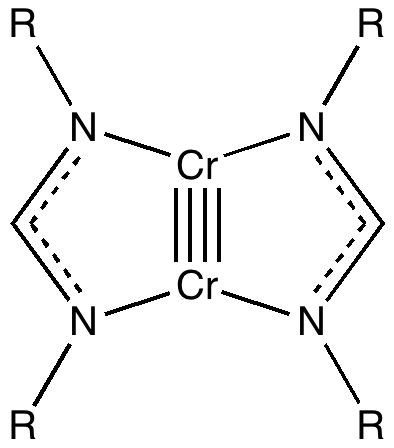
Six years ago, I posted on the nature of a then recently reported[cite]10.1002/anie.200803859[/cite] Cr-Cr quintuple bond. The topic resurfaced as part of the discussion on a more recent post on NSF3, and a sub-topic on the nature of the higher order bonding in C2. The comment made a connection between that discussion and the Cr-Cr bond alluded to above. I responded briefly to that comment, but because I want to include 3D rotatable surfaces, I expand the discussion here and not in the comment.‡
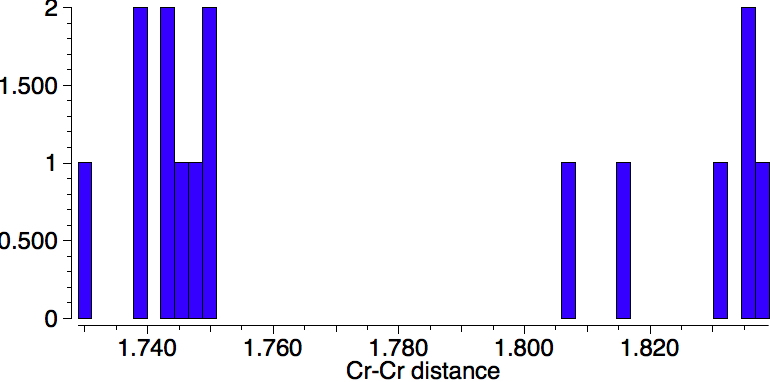
Firstly, a quick update. Since the original post, quite a few Cr-Cr quintuple bonds have been reported. In searching the crystal structure database, I used the text "quintuple" as a text search term (since specifying a quintuple bond as such is not supported) along with a Boolean AND using the sub-structure Cr-Cr (with any type of bond allowed). The result is shown below. It is striking that in fact these "quintuple" bonds cluster into a set with a bond distance of ~1.74Å and another with 1.83Å. Are these valence bond isomers?
Now to the system shown at the top (one of the 1.74Å set). My original post discussed the results of a density functional evaluation of the properties of the electron density in the Cr-Cr region. Most striking was the value of the Laplacian ∇2ρ(r) of this density, the value of +1.45au being the largest ever reported for a pair of identical atoms. I should remind that ∇2ρ(r) is used as one measure of the character of a bond, being the balance between electronic kinetic energy density and potential energy density along a bond. But it is well recognised that the bonding between such transition metals has what is called multi-reference character; the wavefunction is not well described by just a single doubly occupied electronic configuration. More electronic configurations have to be included, and hence a MC-SCF (multi-configuration) self-consistent description of the wavefunction is needed. So as a response to the comment noted above, I decided to carry out CASSCF/6-311G(d) calculations, in which an active space of electrons and molecular orbitals is specified, and using the geometry previously obtained at the DFT level. Thus a CASSCF(8,8) calculation takes 8 electrons and evaluates all possible configurations arising from placing them into an active space of eight molecular orbitals. With metals unfortunately the active space is likely to be large, and so I decided to computed (10,10), (12,12) and (14,14) CASSCF as well to see if any convergence might occur. The last is close to the limit offered by the program. The values shown below are at the QTAIM line (bond) critical point along the Cr-Cr axis.
| Active space | ρ(r) | ∇2ρ(r) | Total energy, Hartree | % of CS config | Calculation DOI |
|---|---|---|---|---|---|
| 8 | .303 | 1.720 | -2383.48049 | 63 | [cite]10.14469/ch/191860[/cite] |
| 10 | .308 | 1.612 | -2383.68830 | 61 | [cite]10.14469/ch/191857[/cite] |
| 12 | .308 | 1.612 | -2383.70398 | 60.6 | [cite]10.14469/ch/191858[/cite] |
| 14 | .308 | 1.612 | -2383.72161 | 59 | [cite]10.14469/ch/191855[/cite] |
| DFT | .313 | 1.45 | – | 100 | [cite]10.14469/ch/4156[/cite] |
From the trend above, we might safely conclude that the CASSCF active space IS convergent, at least for the density if not for the energy. Also convergent are the properties of the density such as ∇2ρ(r), and noteworthy is that the value of this property is even higher than was obtained using single-configuration DFT theory. So the claim that this system has a record such property does not change. Negative values of the Laplacian are normally taken to indicate a conventionally covalent bond, whereas +ve values show the bond has what is called charge-shift character.[cite]10.1038/nchem.327[/cite] So these Cr-Cr quintuple bonds must be amongst the most charge-shifted exemplars!
I show some surfaces (click on the image to get a rotatable model) computed from the CASSCF(14,14) density. Firstly the electron density ρ(r) itself, contoured at 0.25au, showing the high value between the chromium atoms.
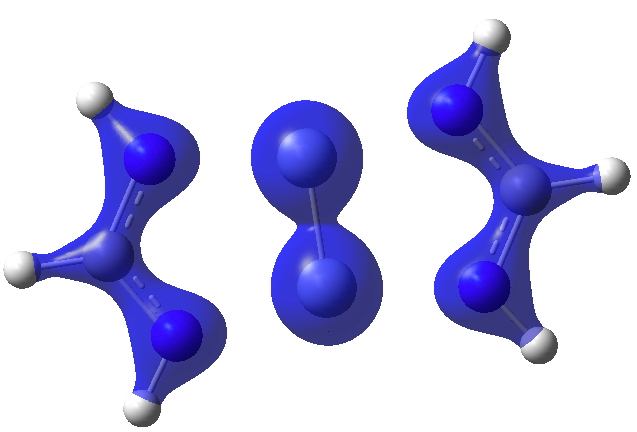
Next, ∇2ρ(r) contoured at ±1.5, revealing its high value in the Cr-Cr region (blue = +ve, red = -ve) and then below at ± 0.25 which includes the covalent bonds of the ligands.
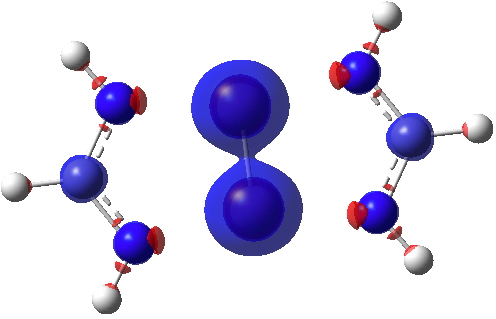
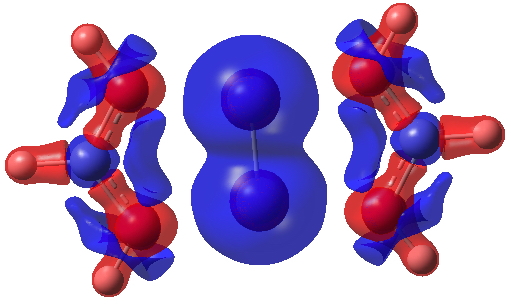
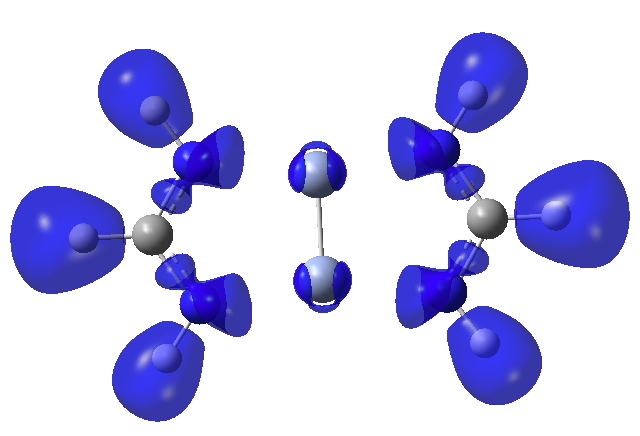
Finally, the ELF (electron localisation function) function which tries to gather the electron density into localised ELF basins (numbers are the integration of the electron density in this basin). This looks very similar to that shown previously and is striking because there is no basin in the Cr-Cr region. Instead, the localisation is along the Cr-N bonds. One might describe this as saying that the Cr-Cr region is very highly correlated.
‡It is a limitation of the WordPress system that such objects cannot be included in comments.
Tags: Chemical bond, chemical bonding, Electron, Electron configuration, energy, Molecular orbital, Multi-configurational self-consistent field, Quantum chemistry, quintuple bond, search term, Transition metal, Valence bond theory
Are those ELF attractors with basin populations 0.16 and 0.22 on the C2 axis perpendicular to the nuclear framework?
Does their existence imply some sort of 'banana bond' character to the interaction between the two chromiums?
Did you calculate the QTAIM atomic populations for the basins of the density, also? That would be interesting to see.
Really, the system looks more like two N3H3 species ligated to a Cr_2 core. I would guess at the Cr-N LCPs of rho, that the electron density is low and the Laplacian is solidly positive.
1. Yes
2. Were it not for the low population, yes a very unusual banana bond, with two layers. The integration was done with a fairly fine grid (300,300,300) to try to avoid integration problems, so its probably real.
3. Since we are discussing the QTAIM delocalisation index, I give here the value of DI=
3.392.1949478 for the Cr atoms. This seems a large value, but it really needs comparison with other systems to properly interpret.4. Indeed. You can get some idea of the Laplacian in the Cr…N regions from the diagram above, which also supports the concept of a Cr2 core surrounded by two ligands.
The full output is published as doi: 10.14469/hpc/241 if more analysis needs teasing out.
Here is another, less restrictive search of the CSD, this time simply for any compound with a Cr-Cr bond.
There are five clusters, with the shortest Cr-Cr bonds at 1.7-1.8Å and the longest at ~3.2Å and apparently three in between.
This does not prove that this histogram contains examples of five different bond orders, but it would be well worth investigating further.
Mo is similar, but with a more diffuse tail.
Isn't a charge-shifted interaction between the two Cr atoms symmetry forbidden in a system like this?
Or, is it allowable due to CASSCF yielding a superposition of two degenerate charge-shifted states?
The latter I think. Certainly F2 has high symmetry, and is perhaps the archetypal example.
Static correlation is so odd sometimes!
Is DFT generally able to give a decent approximation of the ground state of a system like this, despite the static correlation? (I guess perhaps it would only yield one of the two degenerate charge-transfer states..?) Even if so, I would imagine TD-DFT's excited states would be terrible?