The post on applying VSEPR ("valence shell electron pair repulsion") theory to the geometry of ClF3 has proved perennially popular. So here is a follow-up on another little molecue, F3SN. As the name implies, it is often represented with an S≡N bond. Here I take a look at the conventional analysis.
This is as follows:
- Six valence electrons on the central S atom.
- Three F atoms contribute one electron each.
- One electron from the N σ-bond.
- Donate two electrons from S to the two π-bonds.
- Eight electrons left around central S, ≡ four valence shell electron pairs.
- Hence a tetrahedral geometry.
- The bond-bond repulsions however are not all equal. The SN bond repels the three SF bonds more than the S-F bonds repel each-other.
- Hence the N-S-F angle is greater than the F-S-F angle, a distorted tetrahedron.
Now for a calculation[cite]10.14469/ch/191808[/cite]; ωB97XD/Def2-TZVP, where the wavefunction is analysed using ELF (electron localisation function), which is a useful way of locating the centroids of bonds and lone pairs (click on diagram below to see 3D model).
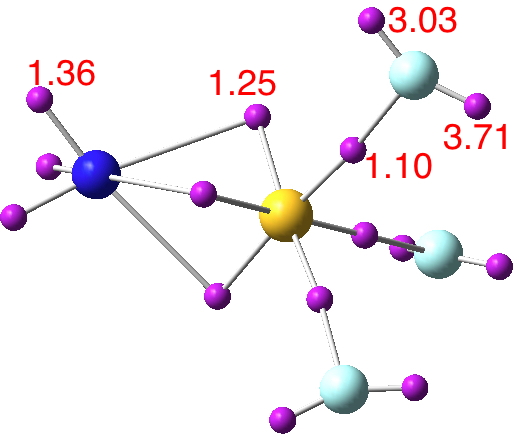
- At the outset one notes that there are six ELF disynaptic basins surrounding the central S, integrating to a total of 7.05e. The sulfur is NOT hypervalent; it does not exceed the octet rule.
- These six "electron sub-pair" basins are arranged octahedrally around the sulfur. The coordination is NOT tetrahedral, as implied above.
- The three S-N basins have slightly more electrons (1.25e) than the three S-F basins (1.10e), resulting in …
- the angle subtended at the S for the SN basins being 96° (a bit larger than octahedral) whilst the angle subtended at the S for the SF basins being smaller (89.9°). This matches point 7 above, but is achieved in an entirely different manner.
- As a result, the N-S-F angle (122.5°) is larger than the ideal tetrahedral angle and the F-S-F angle (93.9°) is smaller, an alternative way of expressing point 7 above.
- The S≡N triple bond as shown above does have some reality; it is a "banana bond" with three connectors rather than two. Each banana bond however has only 1.25e, so the bond order of this motif is ~four (not six) but nevertheless resulting in a short S-N distance (1.406Å) with multiple character.
So we have achieved the same result as classical VSEPR, but using partial rather than full electron pairs to do so. We got the same result with ClF3 before. So perhaps this variation could be called "valence shell partial electron pair repulsions" or VSPEPR.
Tags: Chemical bond, chemical bonding, Electron, Lone pair, Molecular geometry, Octet rule, Quantum chemistry, Stereochemistry, Tetrahedral molecular geometry, Theoretical chemistry, Valence, VSEPR theory
Just to show that this picture can be obtained from QTAIM, I made one graph for you.
To make this figure, I removed sigma orbitals from the wavefunction of molecule (MOs #10, 13, and 23). Sigma orbitals are usually highly concentrated so do not permit that the topology of pi electrons to be detected. The molecular graph evidently shows three equivalent pi-interactions. I have to mention that delocalization index of the S-N bond is 1.99 electrons, comparable with a double bond C-C bond. However, since the S-N bond is polar, the magnitude of DI is reduced from ideal number expected from VSEPR that is 3. Finally, I think it is legitimate to remind of the latest works of Ronald Gillespie in which he explained that VSEPR is in fact a buzz name for Pauli Exclusion Principle. The real factor that determines geometry of a molecule is not valence shell electron repulsion but is Pauli exclusion that pushes electrons with same spin as far as possible from each other.
The real factor that determines geometry of a molecule is not valence shell electron repulsion but is Pauli exclusion that pushes electrons with same spin as far as possible from each other.
Yes indeed it is the Pauli exclusion we are really discussing here (and ELF is another way of tracking that). But most student-level examples do not teach it like that, and instead focus on the electron-pair. This leads to eg the consideration of five pairs (ten electrons) for F3Cl, or if you take the Lewis structure shown for NSF3 at face value, 12 electrons (four σ-bonds and two π-bonds).
Yes, unfortunately, at student's level VSEPR is defined as electron pair repulsion. Again unfortunately, those who study in less-theory-oriented branches of chemistry have no idea about the role of PEP. They keep the notion of electron-pair repulsion as a sacred rule. PEP should be entered into general chemistry text books, I believe.
And to add one further electron localization method, NBO (natural bond orbitals). I will merely summarise the results (DOI: 10.14469/ch/191808) here:
1. Two orthogonal S-N π-NBOs
2. One S-N σ-NBO
3. Three equivalent F-S σ-NBOs.
Which seems to point to six electron-pair bonds around S (NBO integrates these to 11.39e) and very much the Lewis structure shown at the head of the post.
BUT:
4. There are three equivalent F lone pairs each with some F-S antibonding character.
5. There is one N lone pair, again with a node along the N-S bond.
Overall then, one might conclude that there are LESS than six bonding electron pairs surrounding the central atom, attenuated by antibonding character from another four pairs.
This is certainly a fascinating little molecule.
One can reduce this last example down to the di-anion of methane (DOI: 10.14469/ch/191811). It has tetrahedral symmetry (no Jahn-Teller effect), with four equivalent C-H bonds/NBOs and one (spherical) carbon lone pair/NBO. Ten valence electrons surrounding carbon? Of course, this carbon lone pair is antibonding in the four C-H regions. This does help remind us that the octet rule applies to bonding electron pairs.
To make this figure, I removed σ orbitals from the wavefunction of molecule (MOs #10, 13, and 23) … The molecular graph evidently shows three equivalent π-interactions.
So if you QTAIM using only MOs 10,13 and 23, do you then get a N-S σ line critical point (vis BCP) back?
Although no longer seen much, an alternative non-symmetry-adapted represention of double bonds is two equivalent banana bonds. Is NSF3 a three-fold version of that, or something new?
First, I think I should say that the figure in my previous comment is a trap! It does not demonstrate a triple π-bond + one σ bond that is removed, making altogether 4 bonds. It is merely curvature of pi-electrons that look like banana bonds.
Then I should say yes, using those orbitals I get one LCP between S and N.
Please remember that according to IUPAC definition the bond order (on the basis of Muliken MO theory) is sum of all overlap matrices between two atoms. In practice there are many MOs in which S and N have at least a minor overlap -here I had to remove 3 of them to remove σ S-N bond. The sum of all MOs is manifested in the magnitude of the delocalization index that is 1.99 in this case.
If I remove sigma-type orbitals from the system and rerun QTAIM computations, I get DI = 1.33 e that is ~ 0.66 e less than the all-electron wavefunction. This means that those 3 σ orbitals had 0.66 e contribution to the S-N bonding.
The π contribution (1.33 electrons) is the sum of contributions of MOs 15, 16, 20, 21, 24, and 25.
One can play the same game with FNPF3, with a NF higher bond order than one (DOI: 10.14469/ch/191812). The coordination is square pyramidal, with three P-F basins and two N-P basins.
Here are two maxima in π-framework of FNPF3: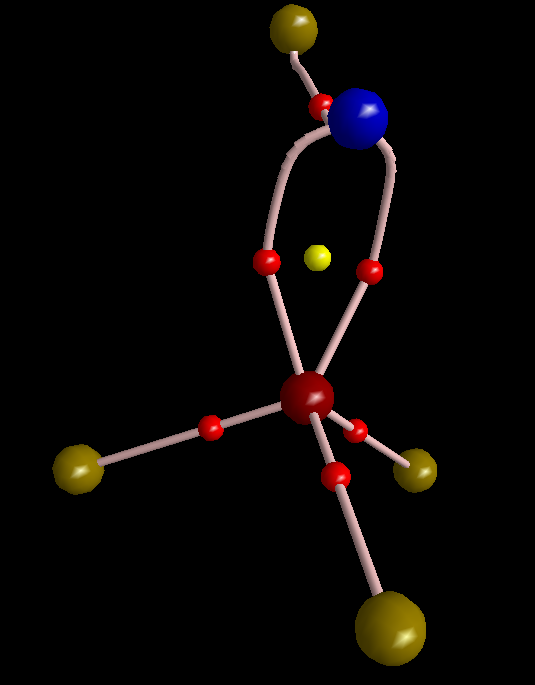
Here I removed three σ-type MOs (15, 19, and 23). The delocalization index of the P-N bond is pretty low compared with S-N bond; it is just 0.88 e and by removing the electrons from the σ-type MOs, DI drops to 0.63 e. The reason for this low DI is the presence of highly polarizing substituent, i.e. fluoride, on the nitrogen. To obtain bond order from DI one must calibrate DI values on the basis of some known examples. For more information please see this paper: DOI:10.1039/C5CP05777A http://pubs.rsc.org/en/content/articlelanding/2015/cp/c5cp05777a#!divAbstract.
Responding to the drop in the DI for the N=P bond due to F on the nitrogen, the obvious system to try next is NPF2 (DOI: 10.14469/ch/191814).
The angle subtended at P for the N-P basins is 149.6° (basin integration 1.82e), closing the angle subtended at P for the P-F basins (integration 1.22e) to 91.2°. The phosphorus is now ~tetrahedral. The NP bond is therefore ~double, and not triple as shown in the Lewis representation. Does QTAIM replicate this?
Another homology of the above would be NClF4. It is a stable species with all-real normal modes and C2v symmetry (doi: 10.14469/ch/191817) but the ELF analysis as well as standard QTAIM make little sense. NBO analysis however does suggest two π bonds between N and Cl. Not sure what is going on here.
The Br analogue NBrF4. (DOI: 10.14469/ch/191818) however is normal, with ~double-bond N-Br character.
I get normal results for F5ClN (wB97XD/def2-TZVP but Cs symmetry … C2v symmetry is found with a little higher threshold). NBO6 analysis with Natural Resonance Theory stuff says, that there are no other important Lewis structures above the threshold … which is different to the first structure in this blog entry, F3SN (there are six and the "main" one has only 29% weight). (I missed to show it, but the bond critical points are only on the "middle" of all five bonds and there is also only one BCP per bond.)
Well … I hope, the picture is included this time.
Thanks Philipp.
1. It is unfortunately not possible in the security model for WordPress blogs, for comments to include images. This is because they could include executable code which is a virus. So I have to manually get the image and insert it as "administrator".
2. MultiWFN (as discussed elsewhere on this blog) is a highly capable wavefunction analyser. Unfortunately, I am running OS X El Capitan which has a new security model. One of the key graphics libraries required to make MultiWFN work on a Mac (OpenMotif) no longer works with El Capitan (even the installer will not install). So my MultiWFN capability has (I hope temporarily) gone.
Amongst the significant differences in the ELF function between MultiWFN and TopMod09 is how lone pairs at halogens are treated. TopMod09 produces normally a pair of localisations basins, whereas MultWFN produces a torus; I think the latter is more accurate and can be seen above!.
Just a note to say I have now got Multiwfn working again. The solution was rather tedious, but involves over-riding El Capitan's System Integrity protection ( http://www.imore.com/el-capitan-system-integrity-protection-helps-keep-malware-away ) and the use of Pacifist to then install the OpenMotif libraries. There are quite a few other non-standard operations, and if anyone reading this wants more details, do please contact me directly.
re BCPs (better perhaps called line critical points or LCPs) are in the middle of all five bonds and there is one BCP per bond only if one looks at the total density. If one removes σ MOs leaving only π-looking MOs, the QTAIM picture is different. This is because the σ density induces annihilations of the π contributions and leaves only an LCP along the bond. See the graphs produced by Cina here!
Both systems were pretty interesting. In case of PNF2 I checked the DI for PN bond; it is 1.89 e for full electron density, which is more than twice the magnitude of DI for PN bond in FNPF3. I think it confirms my speculation about the role of fluoride substituent in polarizing the PN bond. I also removed the σ electrons. The DI droped to 1.25 e. Two LCPs appeared, corresponding to two electron concentration in the topology of electron density of π framework. Also in line with ELF picture.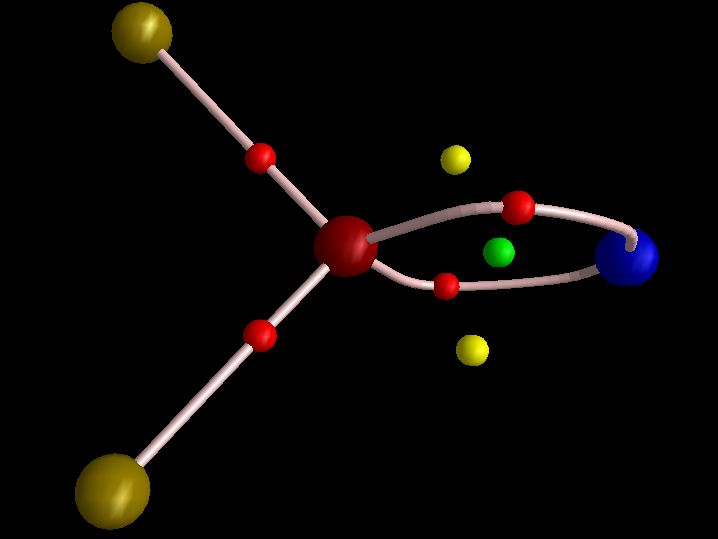
The topology of electron density is absolutely amazing as I see two RCPs. I am not sure if it is an anomaly or something meaningful, but Poincare-Hopf condition is satisfied for the molecular graph. In case of NClF4, I think for some reason your wavefunction is not correctly produced. 
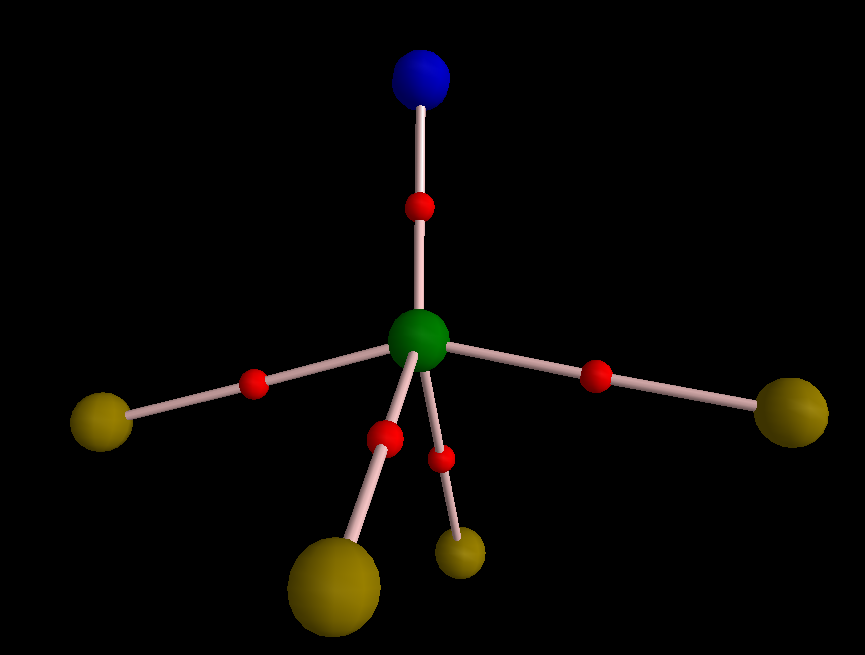The DI between N and Cl is higher than that of PN or SN in the original post; it is 2.21 e. I think the higher DI is the result of proximity of the electronegativity of Cl and N. Thus, Cl-N bond is less polarized compared to S-N and P-N bonds and is more covalent. I removed σ electrons either. Topology of π-framework is fascinating! 
However, unfortunately my AIMAll fails to complete integration as it cannot recognize one of RCPs. So, I cannot say how much DI decreases by removing sigma electrons. You may try it by MultiWFN if you want. Here is π-WFN: https://dl.dropboxusercontent.com/u/51599297/Clf4n-Pi.wfn
Yes, the π topology is indeed fascinating; a four-fold banana bond. One might even be tempted to equate it to a quadruple bond (although I suspect the analogy is false).
I do not know why the WFN file was corrupted (it clearly was), since it works for eg NBrF4 and even NClF3Cl. I did run the calculation three times, changing eg the integral accuracy and the grid size, but all failed in this manner. A deep seated Gaussian bug?
I ran the π-only WFN file you created through TopMod09; it has the advantage that it integrates the basins for electron density (If I remember, MultiWFN does not do this?) and it shown below (π-only).
If I understand the desired calculation correctly, yes, MultiWFN is able to integrate the electron density in the ELF basins:
* Main menu option 17 (basin analysis)
* Generate basins (option 1 in 1st menu) on ELF (option 9 in 2nd menu)
* Once generated, integrate real space function (option 2 in 1st menu) selecting electron density (option 1 in 2nd menu) as the function
One of the frustrating aspects of MultiWFN, though, is tracing back which basin # corresponds to which nucleus and/or non-nuclear ELF attractor. I have plans to write a Python wrapper for it at some point to automate collation of such results, but I've not yet started coding it.
I am unable to use MultiWFN any more. It is built using an OpenMotif graphics library for OS X. Since I updated OS X to El Capitan, that library (which is no longer maintained) does not install (the installer simply now fails) and MultiWFN does not execute.
MultiWFN has many advantages:
1. It is parallelised, and so runs very much faster than TopMod09.
2. Accordingly, it can generate very much finer meshes
3. Basin collection seems to be more accurate than TopMod09.
4. But its graphic interface is relatively simple and it can be quite difficult to orient a molecule interactively.
If anyone has any advice on how to get MultiWFN working again on OS X, I would much appreciate it.
Hm, well, that's irritating.
I looked at the MultiWFN website; there is apparently a new version as of last week, 3.3.9 – but, it appears still to have openMotif as a dependency. No help there.
I would contact the development lead, Tian Lu, at Sobereva–at–sina–dot–com to notify regarding the incompatibility and to solicit advice for resolving it. Hopefully there's another library to which it can be ported.
As re #4, yes, this is a tremendous disadvantage of MultiWFN. I think one can export basins, paths, etc. in various forms (.cube, pdb, etc.) that might be importable to other software (Avogadro, VMD… perhaps Chemcraft?), but it's an annoyance to have to go through the additional steps.
A slight change of tack, but I checked the crystal database for any instances of e.g. N=Cl or N≡Cl (ie higher than a single bond order). There are none.
There are however 35 instances of S≡N (no disorder or error in data). One should remember that the designation ≡ is to a large extent entered into the database by a human and probably does not have any theoretical meaning.
A histogram of SN distances is shown below, revealing there are examples below 1.4Å!
This entry (VEPVES, doi: 10.5517/CCNJ6V6) is the shortest (1.364Å) and is Me-N≡SF3+. SbF6–. This in turn reminds me that if one takes N≡N and protonates it to H-N≡N+, the N≡N bond contracts significantly!
Interesting results! I am not much aware of experimental work on hyper-coordinated halogens but I doubt anyone have tried to synthesize NClF4. It should be very instable, almost an explosive! What you think about publishing NClF4 as the first example of Cl-N triple bond? 🙂
Whilst a Cl≡N triple bond is quite esoteric, the route taken to arrive at that point is perhaps more interesting. Thus the article entitled "One Molecule, Two Atoms, Three Views, Four Bonds?" (coined by the way by Roald) sets out a trialogue almost in the manner of the script for a play (see DOI: 10.1002/anie.201208206). I think its always interesting to experiment with the form of the "journal article". So food for thought there.
I noted above that defining a triple N≡S bond in the crystal search is rather subject to arbitrary classification, and so got to wondering what a search with a double bond specified might come up with. Here it is. Again, there are a few hits < 1.4Å, although the most frequent value is now ~1.55Å, longer than with N≡S.
Back to the start! Here is the ELF analysis for MeNSF3+ (doi: 10.14469/ch/191820). The triple bond basins are now highly populated, and as per usual in this trialogue your π-dissected QTAIM Cina would be useful. And what is going on with that little basin integrating to 0.4e along the SN axis?
This new molecule is really hot! First, though the S-N bond in CH3NSF3 is shorter than that of NSF3, the delocalization index between S and N is "less" than that of SN bond in NSF3. Here the DI is 1.35 e, compared with 1.99 for the SN bond of NSF3.
So, I might say that some sort of ionic interaction between S and N is decreasing the bond length. Or, something is going on that I cannot understand at the moment. I need to think more. I see a short bond with less covalency. Maybe we cannot compare NSF3 and Me-NSF3+…
Anyhow, there are even more interesting things to see. Please see the molecular graph without σ electrons:
Here not only I can see the familiar banana shaped curvatures, but I see also something between methyl group and N that I would like to call it the effect of hyperconjugation! This is fascinating! I think this is the first example that someone showed an electron-density based representation of hyperconjugation.
The DI without σ-framework is 1.18 e that suggests the σ-electrons have a minor effect on the S-N covalency. While in NSF3 σ-electrons had a contribution of 0.66 e, here the σ-framework has only 0.17 e contribution to S-N bond. Where are those electrons? Maybe are shared with carbon. Finally, nothing comes out of electron density analysis to unveil the nature of that attractor near the sulphur atom. Can that attractor explain lower covalency between S and N? Many things to think about till tomorrow!
Cina,
I thought I would have a go at computing QTAIM on just the π manifold. The most obvious thing to try first was to obtain a WFX file (this is a human-readable version of the standard WFN file, + some additions) where the MO occupancy numbers can be easily edited down to zero as desired. But running this edited WFX file through AIMALL produces nonsense.
So might I ask how you dissect the contributions of the MOs to the QTAIM analysis?
In fact WFX is not as easy to work as WFN for disection. I do not use WFX unless 1- I want to check magnetic properties; 2- Deal with an atom with ECP. To remove MOs from WFN you just have to set occupation number of MOs in WFN equal to zero. I am working on your samples. But unfortunately, I catch a cold, stayed in bed and thus computation is slow… Please see one example of manipulated WFN here: https://dl.dropboxusercontent.com/u/51599297/cf3clfn-pi.wfn If in some cases like this species &;sigma; and π are mixed. It's better to remove whatever that resembles a σ orbital.
The normal canonical MOs often mix σ and π very extensively. I am wondering whether one could instead use localised wavefunctions such as NBOs? The trick would be to get eg Gaussian to write out NBOs into the WFN file rather than MOs. This should result in σ NBOs that project out π contaminations and vice versa.
Do you know if the WFN write can be manipulated like this (perhaps via an IOP command?)
Yet another transform; CF3CSF3 is a known crystal structure (doi: 10.1021/ja00050a027), where the neutral CF3C replaces the charged CH3N+. The calculation (doi: 10.14469/ch/191821) shows C3v symmetry, but the out of plane deformation is a low energy one. The C≡S bond length is calculated as 1.430Å.
The CF3N+SF3 isoelectronic isomer of CF3CSF3 (doi: 10.14469/ch/191823) is now bent (156.8°) and the C≡N length is 1.395Å. This bending reminds of Lewis’ 1916 representation of the triple bond in three isomeric forms, one linear and two bent. Whilst C≡C is always found in a linear form, SiSi bonds are bent, and this system is clearly on the edge between the two.
Next, CF3NClF4+ (doi: 10.14469/ch/191824)
And to complete the set, here is CF3CClF4 (doi: 10.14469/ch/191826).
This is a nice idea indeed. In 2009 I searched a lot to do so because I wanted to check the effect of electron density on dissected-NICS. But, couldn't find any trick to do that. Anyhow, for most of your examples σ-π separation was achievable. These non-linear molecules are making a bit of trouble. Meanwhile, please see molecular graph of CF3NCl4: N-Cl DI for full electron density wavefunction is 1.76 e and for π-framework is 1.3 e. Molecular graph seems fine to me, although the molecule is nonlinear.
Here is CF3-CSF3; the C-S DI for the full electron density is 1.99 e, and that of π-density is 1.41 e. I see three banana-shaped π-interactions.
The last example that I checked today is CF3-NSF3. It seems that when molecule is bent, σ-π separation distorts the molecular graph. Please see the MG here: https://dl.dropboxusercontent.com/u/51599297/cf3-nsf6-pi.png The DI of S-N bond is 1.30 e that drops to 0.83 e after removing σ-electrons. I am not happy with the MG of this species. It is a catastrophic MG in Bader's terminology, i.e. a small change in the molecular geometry changes the MG. Please note how close are RCP and BCP in CF3 side. A minor change in the geometry will merge these points.
Yes, it is a topological feature that appropriate pairs of critical points can annihiliate each-other, and so geometric catastrophies are possible. ELF at least is stable to this sort of effect.
P.S. 1; I will check the last system tomorrow. P.S. 2; I am almost sure you have seen this paper but just in case. 10.1039/C5SC04608D
Finally, here are data for CF3CClF4. The π-electron density has a pattern pretty similar to what you obtained from ELF analysis. I noticed that there are some CMOs formed from combination of p-orbitals of fluorine atoms on Cl and σ-type Cl-C MOs. If I keep them in the wavefunction, the final molecular graph looks perfect and those anomalous critical points do not appear. So, it means that I may play with the molecular graphs of the other systems to make them stable (in terms of topology).
It does not affect on the magnitude of DI considerable because the overlap matrix is not big enough to affect the magnitude of the DI. The DI for C-Cl bond in CF3CClF4 is 1.63 e. Removing the σ electrons decreases the DI to 1.12e. What do you think about examining molecules with a negative carbon? This is iso-electronic with nitrogen. Someone may synthesize them as a cesium salt perhaps!
Cina,
The C(-) analogue of N is a known motif in crystal structures; there are four examples known to metals.
1. SIVREV to Os (doi: 10.5517/CCN9Z41 )
2. ROJVOB to Mo (no doi)
3. OGONON to Ru (a Kate Bush song! Almost) (doi: 10.5517/CC6CYL2 )
4. IDOZOQ to Ru (doi: 10.5517/CC61WVY)
Now there is a suggestion. Since single-coordinated carbon (in e.g. C2) can (controversially it has to be said, see 10.1002/chem.201400356 for one interpretation) sustain a quadruple bond, are any of these examples thus? I suspect we might be about to find out!
Now for (-)CSF3 (doi: 10.14469/ch/191831)
Well, I analyzed this system. For the full electron density DI is quite high (2.50 e), comparable with C2. At that time when C2 was in spot light, I checked it with AIM for my curiosity and came to this conclusion that it can't be a quaduply bonded carbon-carbon bond but didn't publish anything. In fact, ethyne has a DI of ~ 3.0. Anyhow, when it comes to heteronuclear bonds polarity of the bond decreases the DI. The DI for π-electron density is 1.84 e. Thus, σ contribution is 0.66, exactly similar to the original molecule, NSF3. Now, let me be a dreamer for a moment. If we imagine that the π contribution to delocalization is comparable with the σ contribution then I should say that my analysis suggests that this molecule has a quadruple C-S bond since 1.84/0.66 = ~ 3 that is three π bonds and one σ bond.
10.14469/ch/191831)
Remember that with C2 itself, the 4th bond can only manifest when multireference character is included. Any density derived from single reference methods will not reveal the 4th bond. There is also very direct experimental thermodynamic evidence that over and above three normal bonds, there is an additional stabilisation of ~17 kcal/mol in C2, and the simplest way of understanding that stabilization is to ascribe it to 4th bond worth 17 kcal/mol. This is strong enough to be called a bond rather than an interaction.
With metals, ie Cr-Cr and other high multiple bonds, again it is correlation only recovered from multireference methods that describe such species properly.
I did check its CAS density indeed but as far as I can remember from the original paper in Nature Chemistry, that 17 kcal/mol stability is with respect to an arbitrary electronic state, i.e. an excited electronic state of carbon with four unpaired electrons in the valence shell. Excitation needs a large energy (perhaps ~ 80 to 90 kcal/mol) that absolutely compensates that 17 kcal/mol. Then, is it really meaningful to call C2 a quadruply bonded carbon? I feel uncomfortable with it. To me MO picture with two bonds is perfect. One can compare C2 with C2H and HC2H to see how the bond length is changing; very simple and clearly the trend is in favour of a doubly bonded C2. Also C2 is isoelectronic with N2(2+); does anyone in chemical community accepts that N2(2+) has quadruple bond?
The topic of higher multiple bonds between C or N and metals is perhaps rather straying from the theme here. But having flagged quadruple bonds, I cannot resist showing one metal system, VADBAD (a nitridocyanomanganese metallate, doi: 10.1021/ic971377h). This has C4v symmetry, and the ELF is shown below (doi: 10.14469/ch/191834). Notice how the ELF basins in the C≡N regions are split into two because of the π contributions. Normally, this splitting may not be observed.
10.14469/ch/191831)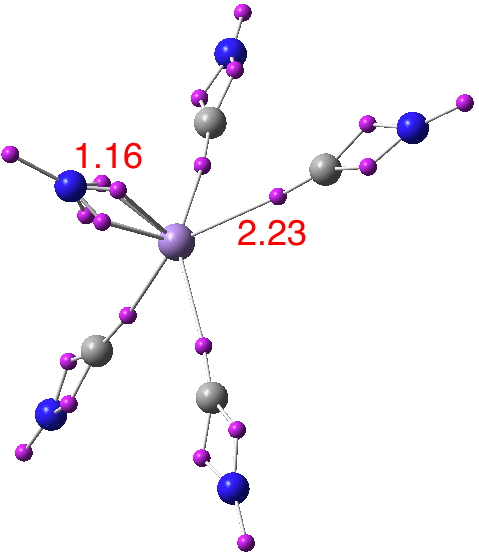
The caveat is that this is a single reference method describing the Mn-N multiple bond character, and should probably be taken with a pinch of salt.
Here is the beautiful π-molecular graph of this complex:
The DI between Mn and N is amazingly large for a polar metal-nitride. It is 2.49 e with 0.72e σ contribution and 1.77e π-contribution. These examples are indeed fascinating due to their large DIs. What do you call these bonds? A triple bond? A quadruple bond?
re I did check its CAS density indeed but as far as I can remember from the original paper in Nature Chemistry, that 17 kcal/mol stability is with respect to an arbitrary electronic state, i.e. an excited electronic state of carbon with four unpaired electrons in the valence shell
Sorry Cina, that is wrong. The 17 kcal/mol is an experimental value for bond dissociation energies leading to C2. The dissociation energy of HCC(.) to CC is measured as 17 kcal/mol less than the dissociation energy of HCCH to HCC(.). The HCC(.) radical is σ state, and localised on just one carbon, and the stabilisation arises from new spin coupling between this radical and the new electron liberated from the second dissociation. In character, it is similar to the spin coupling in [1.1.1] propellane which forms a weak central C-C bond, ie much "longer" than normal C-C bonds. Because this "bond" is longer, its effect on the total electron density is likely to be small, and probably masked. Sason Shaik has gone through other arguments such as Badger's rule for bond length/force constants etc, and resolved them all.
Then I obviously missed this part. No one can argue against the bond energy, I think. I read the original article in Nature Chem. and few follow ups one by you and Roald Hoffmann and the other by Gernot Frenking. The excited C atom was introduced in the original work I remember. So, let's go back to our business; let me check the latest molecule.
I rechecked my old AIM computations on C2. There is something weird there. I am rechecking everything from the beginning by a huge basis set. My old interpretations seem wrong to me.
Time I think to collect all these results into a single table to see if further patterns emerge. Whether this is best done here or elsewhere we might discuss.
Absolutly agree. I am just working on C2. I checked my old data, there was an NNA in between carbons. I also realized I had studied C2 at a DFT level that produces the same geometry as CAS, not at CAS level. Then, I was trying to get it optimized at CAS(8,8)/def2-TZVP level with Gaussian. But, I realized that G09 rev. D02 has a bug with CAS; if you sepcify CASSCF instead of CAS, though technically these methods are the same, Gaussian fills the memory of computer with something that I don't know what it is! Even, CAS(4,4) for ethyne does not proceed with specifying CASSCF with 1.5 TB memory! So, I am now redoing them after realizing how to fix that bug. I hope I can get the data before tonight. Tonight, I am going to Iran and there I will have limited access to Worldpress blogs since they are surprisingly filtered! I can be in touch with you via email.
Finally, analysis of C2 finished. I got it optimized at CAS(6,6)/def2-TZVP level. Concerning the results obtained by Frenking et al (doi: 10.1002/anie.201301485), CAS(6,6) should describe the main part of the wavefunction according to their analysis, performed at CAS(8,8)/cc-pVTZ computational level. I also did the same with ethyne as a reference system (optimized at CAS(6,6)/def2-TZVP). The DI for CC bond in ethyne is 2.20 e. IN C2 the situation is indeed very complicated and open for debate! I found two NNA in between C atoms. Please see the MG and plot of del^2Rho for this system here:
These NNAs contain 0.83 e. One may say these electrons are indeed a part of shared electrons between two carbons. Then the DI betwen two carbon atoms is 1.48 e. Of course less than that of ethyne. Each carbon shares some electrons with each NNA too. Also, NNAs share some electrons with each other. The sum of all shared electrons in the molecule is 2.91 e but this includes NNA-NNA and C-NNA interactions too that I have no idea what to say about them. However, if we say since NNAs are in between two carbons then their sharing can affect CC bonding and increase the CC bond order. I cannot manipulate WFN of CAS since orbital populations are evidently fractional. So, I can just speculate that these NNAs might be related to those free electrons of the C2 molecule. One may look at the situation differently. You can say the bond order is sum of DI between CC and the population of NNAs because NNAs are between C atoms, thus have characteristics of the "shared electrons". Then total number of shared electrons will be 2.31 e, again larger than that of ethyne.
I will perform one final analysis within the context of IQA theory of Pendas et al. Let's see what may come out of that one.
I have seen NNA (non-nuclear attractors) between atoms previously (most famously in F-F), but never two. As you say, interpreting QTAIM with fractional orbital occupancies coming from multireference states is "unexplored". But clearly C2 is different from HCCH, and continues to spring surprises!
I had seen examples with more than one NNA between two atoms. B3+ at DFT level has a strange molecular graph with more than one NNA between two atoms. But again, such cases are not systematically studied. I cannot say that those NNAs are not just an artifact in the electron density of B3+. Even here who knows, increasing the basis set size may removes these NNAs. Or an FCI treatment or even CASPT2 may results in a different molecular graph. There are many unexplored things about tiny molecules like C2. Unfortunately, grant agencies do not pay for such studies!
In chemistry we are application-oriented as you know well; but in physics, they know how to admire the elegance of phenomena and do not care how much it may cost to build a megamachine like LHC.
One technical comment; it is always worth increasing all program accuracies on SCF and two electron integrals for such cases.
I can fully replicate Cina's CASSCF(6,6)/Def2-TZVP QTAIM result for C2 (below, all electrons included, doi: 10.14469/ch/191848). The two NNA's are surrounded by three LCPs, but they are quite close and two annihilations would indeed leave just a single LCP (BCP), which is the normal result along a bond. So there is little doubt that C2 is most unusual in this regard.
A similar result is obtained for the isoelectronic B22- (doi: 10.14469/ch/191847)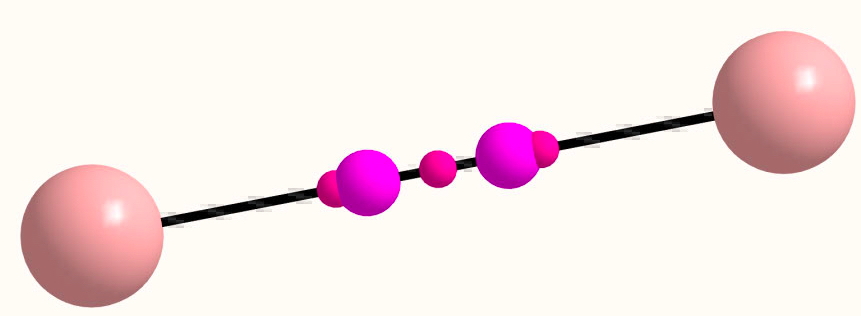
The equally isoelectronic N22+ is however different (doi: 10.14469/ch/191846):
We also did AIM for C2. C2 has at least two charge-shift bonds (the π bonds) if not three (the weak bond). Charge shift bonds have these strange AIM features.
Sason
May I ask you if you have published your results, let me have its DOI?
I have to add that the pattern in the Laplacian plot is related to the atomic shells. Each atomic shell has a charge concentration and a charge depletion region. The best examples to check are noble gases. You see these regions for helium to any noble gas that has an all electron basis set. Besides, I checked delocalization index for C2 at CAS (8, 8)/def2-TZVP. It has basically the same values as that of CAS (6, 6). The DI differs in the second digit after the point.
It's a good point. The small effects we are looking for may indeed be masked by the larger effects of the atomic shells.
I am not sure how the VB concept of charge shift bonding can be defined within the context of AIM but if you are looking for charge concentration/depletion regions, you may look at the ∇4ρ(r), Laplacian of the Laplacian, to see minute changes in the electron density distribution. It is available in AIMAll, I think. Though, no one used it yet for such a purpose.
I note Sason has now joined in. I just checked with him about N2(2+), which I did recollect was done a few years ago along with the original C2 work. He tells me that N22+ "has an even stronger 4th bond than C2 (simple electronegativity effect)". Yes, a characteristic of charge-shift bonds are NNAs, and in ELF they manifest by bifurcating the ELF basin into two, as with fluorine. In C2, this bifurcation seems to be extreme.
Yes, Henry, we are back to charge-shift bonding in this molecule. We were delayed because of the controvercy with the coalition, but we might get back to it after the paper I sent you is accepted.
We'll definitely be in touch.
Sason
Since we have been discussing multireference methods (for C2), I thought I might check on any such character for the molecule which is actually the topic of this post, NSF3, 96% of the wavefunction is in fact the closed shell one. In contrast, C2 is 73.2%, N22+ is 68.7% and B22- has two dominant configurations, each 47%.
Henry, Did you check the Laplacian for C2? Sason
Regarding the Laplacian, I should first explain that the QTAIM (and also the ELF basin centroids) reduce down to a point along the C-C axis (they are obliged to be axially symmetric). At the QTAIM LCP/BCP (3,-1) centroids, the ∇2ρ(r) values are -0.29 (twice) and -0.72 for the central point (CASSCF(8,8)/Def2-TZVPP calculation, doi: 10.14469/ch/191851 and 10.14469/hpc/222). These appear to be normal "covalent" values. The full Laplacian function takes the form of a torus surrounding the central bond and the following best shows the properties of this function in three-dimensional space (red = -0.6 for ∇2ρ(r), blue = +0.6).
You can see other examples of this function for ethane and benzene for comparison here.
For completeness I also include the ELF function, contoured at a value of 0.82, which is again axially symmetric.
I should add to my last comment that the value ∇2ρ(r) at the mid point of the CC bond probably reflects mostly the "normal" first σ-bond rather than the much weaker 4th bond. If the 4th bond does "bifurcate" (a long weak bond), then the value of ∇2ρ(r) closer to the atoms may be a better reflection of its properties than the mid point.
Here is another view of ∇2ρ(r), this time at an isosurface value of +0.1. The blue torus around the bond arises from the π-electrons, for which the ∇2ρ(r) is +0.1. This tends to suggest that the π-torus has charge-shifted character which is not observed along the bond-axis. There is of course another region of +ve ∇2ρ(r) which is fully enclosed inside the red (-ve) region. This also serves as a reminder that QTAIM values at the centroid (along the bond axis) may not properly reflect the full region of space.
I am a bit skeptic about the idea that this figure is related to charge shift nature of pi-electrons. You may get a similar figure from ethane's C-C bond. Please see the figure that I had produced for the profile of the ∇2ρ(r) of C2 in my comment above. The same type of figure can be made for any bond having a shared character, i.e. negative ∇2ρ(r) in the bond's LCP.
Might I suggest another approach? Computing the difference in properties between the closed shell CASSCF singlet and the open shell CASSCF triplet. This should reveal differences induced by the spin coupling of just these electrons (i.e. the putative 4th bond).
If e.g. the Laplacian were computed for both states and the two cubes subtracted, it might reveal something interesting?
I did try a CASSCF calculation with triplet spin state specified (and the resulting energy was ~15 kcal/mol higher than the singlet) but clearly a new trick is needed to write out the WFN file in appropriate open shell form? My WFN appeared to be for the closed shell natural orbitals.
I would also comment that using just CASSCF (which includes only static, and incomplete dynamic correlation effects) might also be influencing things. As you point out Cina, a CASPT2 approach (which does include both static and more complete dynamic correlation) might be needed.
I am not comfortable with electron density difference maps. Indeed, you cannot get a precise physical insight out of them. To make such a map, you should first violate PEP, that means introduction of an unphysical reference state. It can make a big trouble in some cases.
Density difference maps have been used in conceptual DFT, by eg Paul Ayers. One of his examples is the density difference map for FCCF and its cation; removal of an electron actually increases the density along the sigma nodal planes. You can see a picture of this here. I do not know of any difference maps for the Laplacian of the density.
I do agree that difference maps are pretty popular but popularity does not change physical principles. In such a delicate case I do prefer not to introduce any arbitrary reference state. About the difference maps of Laplacian you are right, I have not seen such a map either. About wfn of triplet C2, have you tried converting fchk to wfn? If you write fchk by density=current keyword, it should remain as it is. Then you can use fchk for AIM analysis directly.
Since the total density is in principle a directly observable property, I am not sure I understand the issue regarding reference states?
Re: use of .fchk files. This might be fine for QTAIM, but the Topmod09 ELF program does not accept them. But I am trying one or two other things.
You can convert fchk to WFN/X by means of AIMAll, then use the wfn/x for ELF computations. About difference maps; comparing the density of singlet and triplet species seems OK to me but many subtract an arbitrary density from a particular density. For example, subtract density of two fragments of a complex from that of the complex. In such cases the sum of fragment densities violates PEP. Though, as I confessed now, I see no violation of PEP in this case. I am sorry, but responding while I am in a party is a bit difficult. Some times I need to concentrate that is very difficult now!
Thanks for the tip. In fact this helps isolate the issue to the program being used to subtract two cubes (cubgen). The individual unsubtracted cubes display more or less OK. Thus the CASSCF(8,8)/Def2-TZVPP Laplacian for the triplet C2 is shown below. It contains an extra feature exo– to the bond, where the two unpaired electrons take up residence. This additional feature has a -ve Laplacian (red).
You can find the position of unpaired electrons by analyzing alpha-electron density. Please see (DOI:10.1039/C5CP04280A). Laplacian of alpha electron density should be intriguing! Sorry, I have no access to computational facilities now otherwise I would do it myself.
Sometimes, there is "behind the scenes" stuff going on. Cina asks about analyzing the α-electron density. The keywords (in Gaussian) for obtaining this would be
CASSCF(8,8)/Def2TZVPP output=wfn pop=NOAB density=current
which should write the appropriate WFN file containing natural orbitals for both α and β density suitable for further analysis. I have however hit a problem with this approach which is currently being resolved, currently with no precise timeline for solution. So I cannot provide the analysis as per above just yet.
Thank you for considering my comment. However, you don't need to obtain separated wfn for the alpha electron density. The information already is encoded in the wfn file that you made from fchk. AIMStudio can perform analysis on alpha, beta, and spin density on an open shell wfn. Laplacian of spin density has also unique features. It shows you the shape of orbitals that unpaired electrons are in. Please see the same paper that I addressed above on U2@C80.
The problem is a bit deeper than that, since the .fchk file I generated does not seem to carry the information either (and hence it cannot be propagated to the wfn). This seems to be associated with the CASSCF keyword, since its not a problem with DFT or HF. There was no problem for example with obtaining the spin density for the electride properties shown on this blog.
More analysis of the above point. A CASSCF function uses (spin) restricted or RO formalism, and does not write out separate density matrices for the alpha and beta spins. QTAIM and ELF require UHF (spin unrestricted) style density matrices for open shell systems to be present in the WFN (or FCHK) outputs. To quote an expert I consulted "code will have to be written".
Henry, Cina: What I picked up from the discussion is only one sure thing: the density for C2 is larger than in HCCH. But what kind of Laplacian elludes me. For me the laplacian is a probe of the balance of kinetic energy (density) vs. potential energy (density). If it can apply bond-wise, then it is helpful. I recall by the way Henry, a quintuple CrCr bond you looked at with a whoopingly large positive Laplacian. Sason
Re Quintuple bond. Yes, that was obtained using single-reference DFT (∇2ρ(r) +1.45). I think it seems agreed that Cr-Cr bonds really do have to be treated with multireference methods (probably more so than C2). But then the size of the active space becomes the question, and whether dynamic correlation also needs adding in.
I rely on a parameter for bonding analysis that measures sum of all overlap matrixes between a pair of atoms, the delocalization index within the context on AIM. However, presence of two NNAs between two C atoms makes the analysis indeed complicated. I tend to say that comparing ethyne, C2 has more electrons shared. Please see this paper for a non-technical explanation on DI and its relation to covalency: http://pubs.rsc.org/en/content/articlelanding/2015/cp/c5cp05777a About Laplacian, I prefer to look at Laplacian from the perspective that Paul Popelier looks at it. Laplacian is a magnifier that shows where electrons are concentrated, where thay are depleted. My coleagues and I at least in one particular case could show the shape of orbitals on the basis of Laplacian: http://pubs.rsc.org/is/content/articlehtml/2015/cp/c5cp04280a see these figures:
I expect that analyzing the spin density in C2-triplet shows the position of single electrons.
We briefly departed from C2 (and NSF3) to consider an old analysis of mine on a Cr-Cr quintuple bond. There I now tried out a CASSCF(14,14) calculation to try to include as much of the active space as possible. Emboldened by its success (i.e. the program did not crash, and successfully converged to a solution), I thought I might as well try out a CASSCF(12,12)/Def2-TZVPP calculation on C2 itself (doi: 10042/196111). I was surprised to find that the QTAIM simplified; the two NNAs in the previous density vanished, and now we have a regular result of just a single LCP (BCP) along the axis. So Cina, given the complexity you mention above is now simplified, can you tell us what the QTAIM now shows?
On a separate issue, to recover all the dynamic correlation in a system, one can try a complete CI. A CASSCF(12,12) is not such a complete CI of course, because it does not include the majority of the unoccupied virtual orbitals. It does however include all the occupied ones, including all the cores. So how much if any dynamic correlation does such a semi-complete CI actually recover (as distinct to the static correlation from the multi-reference character).
I am closely following your blog but unfortunately I am currently connected to the web via my mobile phone. If you can kindly check the value of delocalization index for CC bond then we can compare it with that of ethyne and see whether DI of C2 is larger or that of ethyne dominates. The DI value for ethyne is given above for CAS (6, 6) computation. I don't think that increasing the active space affects the DI value of the ethyne much. If it changes, it should decrease. Now, if the DI for C2 at CAS (12, 12) is larger than that of CC bond at CAS (6, 6), we can safely say C2 has a bond with higher order than three. Otherwise I would perform a larger CAS computation for ethyne.
I leave a comment regarding CrCr bond here. Like C2, I would definitely check the DI value for CrCr bond from the SUM file of the AIM computations. To the best of my knowledge DI is the best and the most straightforward index of bond order within the context of AIM theory.
Reading my own comment, I noticed I wrote it a bit unclear. By analyzing the spin density of triplet C2 one must find the shape of atomic orbitals in which single electrons are placed. Anyhow, could you get the wave function of triplet C2? If not, what that Laplacian map in these comments is referring to. Isn't it triplet C2?
The triplet diagram I put up was approximated by a closed-shell natural orbital WFN, with occupation numbers of ~1.0 and ~1.0. I argued that since one must square the coefficients to get the density, this open shell "singlet" would give a similar Laplacian to the equivalent open shell "triplet". As I indicated elsewhere, the program will need code written to write out a proper open shell WFN file for the triplet.
I wanted to follow up Sason's comment about Cr-Cr with an evaluation of whether a CASSCF calculation, along the lines we have been discussing for C2 and other species, might change the value of ∇2ρ(r) for the Cr-Cr system. Its a bit too long to include here, and so I have posted instead.
Can you do MRCI?
If so, then MRCI/6-31g* is almost as good as FCI with the same basis set.
Sason
For efficient MRCI calculation, the commercial programs MOLCAS or MOLPRO are probably best. The free programs FIREFLY, GAMESS and ORCA also have the capability. Of these, we really only have access to ORCA here on our high performance cluster and I have no experience of the MRCI modules.
Well, I connected my mobile phone to our computational resources, thanks to diverse number of apps that provide SSH connection, and performed AIM computation on C2 wave function, obtained at CAS(12,12). The AIM computations were fast and extremely accurate (the Lagrangian of atom that is -1/4 atomic integral of Laplacian is only 8 x 10^-9; the smallest Lgrangian I have ever seen).
However, delocalization index between C atoms is smaller than that of CC bond in ethyne. It is just 2.1 e (compared with 2.2 e for CC bond in ethyne at CAS(6,6)/def2-TZVP level). This result is not convincing for me yet. As the active space grows larger, the correlation between electrons increases thus alpha and beta electrons cannot delocalize as easily as they did at a non-correlated/weakly correlated method. That is why delocalization index decrease by increasing the electron correlation. Here, I think the only way to solve this mystry is to obtain wave function of ethyne at the same level as C2. So, we need CAS(12,12)/def2-TZVP wave function for HCCH. I could not go further than CAS(6,6) for C2 and HCCH on our systems since we have a limitation of ~ 5 TB for memory usage. I could not get a CAS(8,8) wave function for C2 with 5 TB of memory. How about you? Can you get the wave function of HCCH from CAS(12,12)?
Indeed, the total DI for the CASSCF(12,12) wavefunction is 2.102. I will add that for HCCH shortly (due to a power failure in our computer room, no calculations have been possible for about 24 hours).
I might also be able to manage a CASSCF(12,14) for C2 itself before our computers refuse, thus adding in a bit more of the virtual orbitals.
A CASSCF(12,14)/Def2-TZVPP calculation for C2 (probably the practical upper limit) gives DI = 2.1204 (doi: 10.14469/ch/191870). Only missing now is the effect of any further dynamic correlation, achievable from e.g. a MRCI (multi-reference configuration interaction).
Here are QTAIM results deriving from a CASSCF(12,12)/Def2-TZVPP calculation on C2 and HCCH, including full geometry optimisation at this level.
1. Data for C2 is published at doi: 10.14469/hpc/242 and 10.14469/ch/191866, DI(A,B) = 2.09967
2. Data for HCCH is published at 10.14469/hpc/243 and 10.14469/ch/191867, DI(A,B) = 2.18559
So Cina's values above are replicated, and we may take these values as convergent for the active space.
But I remind that the two electrons derived from half of the covalent H-C bonds are going to be a weak perturbation. Any 4th bond formed by spin coupling of this electron pair may have different (i.e. charge shifted) character from the underlying covalent bond, and to me the correlation between such an electron pair and the DI remains to be established. What for example is the DI for F2, another charge shifted bond?
I performed an additional analysis on C2 and HCCH molecules using IQA (interacting quantum atom) method of Pendas et. al. There was a minute chance that in C2/HCCH the electron sharing/exchange-correlation energy has a particular non-regular relationship. Let me explain what I am talking about. First, IQA analysis is if not the most accurate, for sure one of the most accurate bonding analyses. It does not invoke any arbitrary reference state and/or does not introduce any non-physical state/energy component. Thus, following Occam's razor, I tend to say this analysis is the most accurate energy-based bonding analysis. Within the context of IQA one can define a first order relationship between the delocalization index and exchange-correlation energy, DI/r = m Vxc; where DI is the delocalization index, r is inter-nuclear distance, Vxc is the exchange-correlation contribution to the binding energy and m is a universal constant see (DOI:10.1039/C5CP05777A and DOI: 10.1039/C5CP05222J). In certain cases DI and Vxc that are electronic and energetic measures of covalency within the context of QTAIM/IQA analyses do not follow the above mentioned relationship. Unfortunately, here this is not the case (if it was, it would be absolutely amazing). Here are exact energy-based bonding analysis of C2 and ethyne: C2: Vxc : -5.8199131018E-01 au Vne + Ven: -2.8927657586E+01 au Vee: 1.3219363532E+01 au Vnn: 1.5263919917E+01 au HCCH (CC bond): Vxc: -6.2956199228E-01 au Vne +Ven: -3.0351391878E+01 au Vee: 1.4145927949E+01 au Vnn: 1.5700902141E+01 au Vxc, Vne/en, Vee and Vnn denote exchange-correlation, nuclear-electron and electron nuclear attractions, electron-electron repulsion and nuclear-nuclear repulsion energies, respectively, defined within the QTAIM atomic basins On the basis of DI and Vxc analyses I would say that either C2 does not have a quadruple bond or though very unlikely, QTAIM is not a proper theory to identify the forth bond of this system. I have to read all literature of C2 to see which side can convince me 🙂 My analysis is against quadruple C2, unfortunately.
A reminder that the enthalpies of HCCH, HCC(.) and CC are all known, and indicate that it is easier to remove the second HC than the first by about 17 kcal/mol. If the theoretical analysis cannot reproduce this by the means above, then there must be some missing component in the theoretical analysis (or there is some unsuspected error in the measured thermochemistry).
I went through a paper by Frenking and Hermann DOI:10.1002/anie.201301485 that discuesses several factors including bond length, bond dissociation energy (the ~17 kcal/mol stability of the supposedly forth bond of C2) and force constant. Actually, I find their discussions pretty convincing and in line with the conclusion on the basis of QTAIM/IQA analyses. In fact, I think C2 is way different from the classical picture that simple MO analysis provides for this molecule, i.e. a doubly bonded system; it is not even similar to a triply bonded ethyne! The story of C2 reminds me a story by Rumi, Perisan poet. He says four friends, one Persian, one Turk, one Greek and one Arab had some money and wanted to by grape but since they did not know the meaning of grape in other languages they were arguing for a long time on the same thing! In my humble opinion the forth bond indeed forms i.e. fourth electrons couple weakly. However, since the fourth elecrons are "almost free" (very weakly coupled) and hence pretty much delocalized around the nuclei of their own atoms (in AIM sense) they seriously affect the "triple bond" between two carbon atoms of ethyne. The immidiate effect of these free electrons is "localization" of bonded electrons. Thus, in C2 we have a forth bond that strongly weakens a triple bond; it is an ironic situation! Now, VB counts the number of electron pairs and finds four couples. In the meantime AIM measures DI but finds less DI than ethyne because the forth electron interferes with the other three and localizes them as a result of PEP. The localization of electrons elongates the bond and lowers the force constant too. Therefore, anyone who looks at force constant/bond length as a measure of bond order will be confused. Now, I think I understand why Prof Shaik says C2 is quadruply bonded and I understand why others cannot accept it. It is a linguistic problem. Please correct me if I am missing something.
I forgot to mention about the DI value for F2. I looked at my old data and found F2 optimized at B3LYP/aug-cc-pVTZ level. Its DI was pretty large (~1.2 au). Of course, DFT is not comparable with CASSCF but in general DI for F2 is bigger than that of ethane at DFT level. DI of ethane is almost unity.
A CASSCF(14,14)/Def2-TZVPP calculation with optimized geometry for F2 (doi: 10.14469/ch/191869) gives a value for DI = 0.88637, or rather less than unity.
I am not surprised about small DI of fluorine molecule. As I mentioned before by inclusion of correlation between alpha and beta electrons they tend to localize more and more thus the delocalization index drops significantly. Therefore, for a meaningful comparison one must compute DI for two molecules at the same level of theory. If we want to compare DI of F2 with that of ethane as a stereotype of singly bonded system we must have DI of ethane at a CASSCF level comparable with that for F2.
I have done a CASSCF(6,6)/Def2-TZVPP calculation on [1.1.1] propellane, which is perhaps the most analogous system to C2. DI for the central C-C bond is .546 whilst that for a normal "covalent" C-C bond is .965. A CASSCF(12,12) calculation is running (added: central DI, 0.531, Normal CC 0.964)
I am not sure we can ever find a molecule that is a real analogous of C2. Please see my comment above.
One test for my hypothesis that fourth electrons localize bonding electrons:
How the C-CH2 bond lengths change between [1.1.1] propellane and tricyclo [1.1.1] pentane (I am not sure about name please forgive me if I use a wrong name; I mean the hydrogenated analogous of propellane).
If the weakly coupled electron localizes bonding electrons of C-CH2 bonds, then the C-CH2 bond lengths must increase and their DI should decrease from tricyclo [1.1.1] pentane to the propellane analogous.
Hi Cina, If you ge me an eamil I will be happy to send you the last paper on C2 (to be published in Chemistry Eur. J). If you have time to read it, you may be convinced that there is a quadruple bond and this quadruple bond reproduces the properties of the molecule. And you may find out that the model of Frenking (double bond with some weak dative bonds) collapses to the quadruple bond. As I told Henry, VB gives you a snapshot of the bonds as electron pairs, each lowering the energy of the molecule. I am less convinced by bond indices of various types. Sason
Hi Prof. Shaik, It's my pleasure to know more about this molecule from your point of view. What do you think of my idea of interfering fourth electron? I am almost sure that C2 is not a 2 +1 bonded system as Frenking et. al. say. But it is highly possible that a fourth electron can localize bonding electrons so C2 has 3 moderate + 1 weak bonds not 2 strong + 1 moderate bonds. Discussions on the basis of bond energy can be misleading because bond order-bond energy relationships are not that straighforward. Here is my e-mail address: canyslopus[-at-]yahoo.co.uk. I just replaced @ with [-at-] to minimize risk of receiving spams from machines that look for email addresses on web.
It is a pleasure to read the curiosity-driven conversations of my colleagues!
I also concur in that we need to understand what a "bond index" means, and that it might not always mean what it seems. Thus, Sason reminded of a quintuple bonded Cr-Cr system I had taken a look at a few years back. At the CASSCF(14,14)/Def2-TZVPP level, this ultra-short "quintuple" bond has a DI(A,B) = 2.195, practically the same as C2. So again driven by curiousity, I am runnning a CASSCF of the type we have been discussing on Cr2 (a molecule notoriously driven by electron correlation). The result might not be directly comparable to the molecules here, but it should be interesting!
It is indeed an interesting coinsidence. I should mention that the magnitude of DI cannot be used as a measure of bond order in the same sense that one cannot use bond energy as a measure of bond order. In both cases we need a reference system. For a detailed discussion please see this paper (DOI:10.1039/C5CP05777A) on the nature of anion-pi bonding (a supposedly noncovalent interaction that seems to be pretty covalent).
Yes, reference systems (or states) are always unsatisfactory, perhaps especially so with any molecule that has unusual/unique bonding that is not directly comparable.
Here are a belated two further systems, NArF3 (doi: 10.14469/ch/191878) and NKrF3. (doi: 10.14469/ch/191877). The ELF analysis gives both octahedral coordination, and as with the previous systems the delocalisation index DI(A,B) is large. One may again presume multiple NAr and NKr bonding.
Henry, Is there a take home summary about DI, Laplacian, ELF, etc.? May be time to summarize. .. Sason
Yes Sason, lots of results on two basic types of molecule, the X~ZFn systems (X=C, N, Z = P,S,Cl,Ar,Kr) and then the very different C2 (with its own problems). As you say, a summary is needed.