Henry Rzepa's Blog

The BBC TV quiz series Mastermind was first broadcast in the UK in 1972, the same time I was starting to investigate the mechanism of diazocoupling to substituted indoles as part of my Ph.D. researches. The BBC program became known for the catch phrase I've started so I'll finish; here I will try to follow this precept with the project I started then. In 1972, one measured the rates of chemical reactions to gain insights into the transition state kinetic model. To obtain more data, we used isotopes such as ²H or ³H, together with substituents such as R-t-butyl to modify the potential energy surfaces of the reactions by inducing steric effects.[cite]10.1039/P29750001209[/cite],[cite]10.5281/zenodo.18777[/cite] We found that the kinetics for this reaction were actually complex^‡ (in part because of pH dependence) involving a Wheland intermediate (the formation of which is shown with red curly arrows above) followed by the collapse of this intermediate to the diazo-coupled product (blue arrows). Coupling to 2-methyl indole (R=X=H, R'=Me), 2-t-butyl indole (R=H, R'=t-butyl) and 4-methyl-2-t-butyl indole (R=Me, R'=t-butyl) revealed that the kinetic isotope effects induced by replacing H by D or T were "not apparent" (i.e. close to 1), the inference being that the rate constant k₁ for those systems was slower than k₂; the formation of the Wheland intermediate was rate determining (the rds) for the reaction. But with 2-methyl-4,6-di-t-butyl indole (R=t-butyl, R'=Me) this changed and a deuterium isotope effect of ~7 was observed. The rate determining proton removal from the Wheland intermediate k₂ was now slower than k₁. With 2,4,6-tri-t-butyl indole, we ended by noting that the reaction become almost too slow to observe and furthermore was accompanied by loss of a t-butyl cation as well as a proton. At this point we attempted to infer some transition state models consistent with these observations. Note that we had relatively little data with which to derive our 3D models (one needs to define a geometry using 3N-6 variables, along with its relative energy and force constants). The text and diagram of our attempt is shown below. 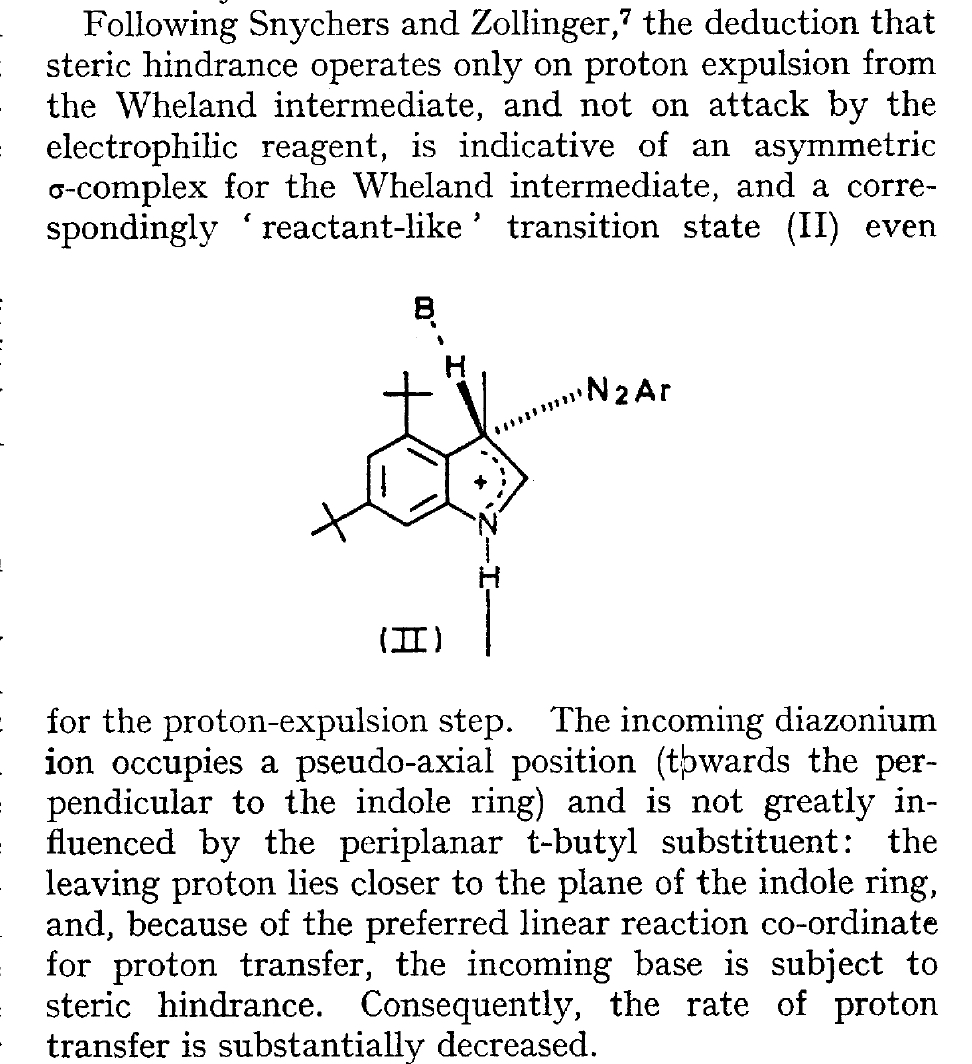The main points of this argument were;

1. That the Wheland complex is asymmetric, with the diazonium ion adopting a pseudo-axial line of attack.
2. In contrast, the leaving proton lies closer to the plane of the indole ring
3. The abstracting base experiences "steric hindrance" if R = t-butyl but not if R' = t-butyl.

I was eager to find out how one might test these models by quantum computation and my next stop in 1974 was to Austin Texas, where Michael Dewar's  group was soon to break the record for computing the geometry of a molecule with 49 atoms (similar in size to the reactions shown above) using the then very new semi-empirical MINDO/3 valence-shell quantum theory. The theory still needed much improvement in a great many aspects and the last forty years has brought us features such as density functional theories, far more accurate all-electron basis sets, superior geometry optimisation methods for transition states, code parallelisation, solvation treatments and increasing recognition that a particular form of electron correlation associated with dispersion energies needed specific attention. These methods would not have become applicable to molecules of this size had the computers themselves not become perhaps 10 million times faster during this period, with a commensurate increase in the digital memories required and decrease in cost. Time then to apply a B3LYP+D3/Def2-TZVP/SCRF=water quantum model to the problem. Four species were computed for each set of substituents; the reactant, a transition state for C…N bond formation (TS1), a Wheland intermediate and a transition state for C-H bond cleavage (TS2). The relative free energies of the last three with respect to the first are shown in the table below. An IRC for R=R'=H (below) was used to show that a bona-fide^† Wheland intermediate is indeed formed.[cite]10.14469/ch/191707[/cite]

IRC animation for TS1, R=R'=H
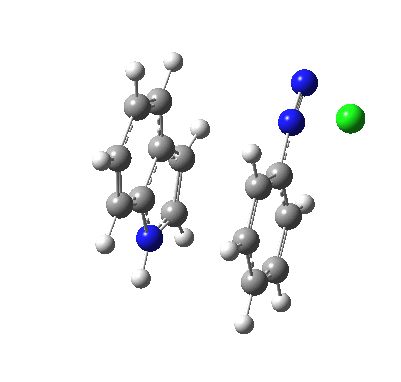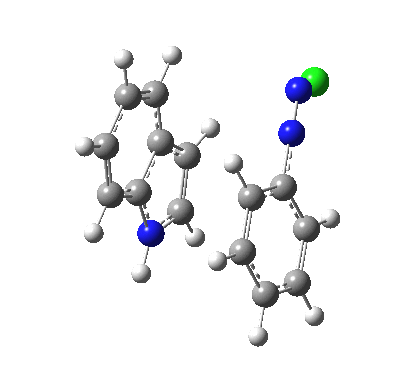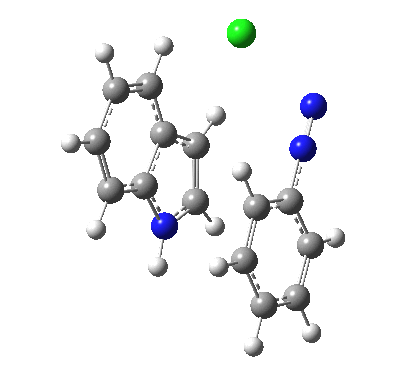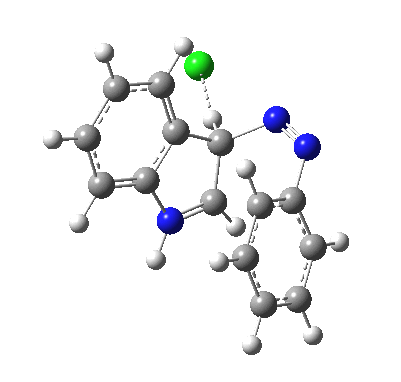
IRC for TS2, R=R'=H

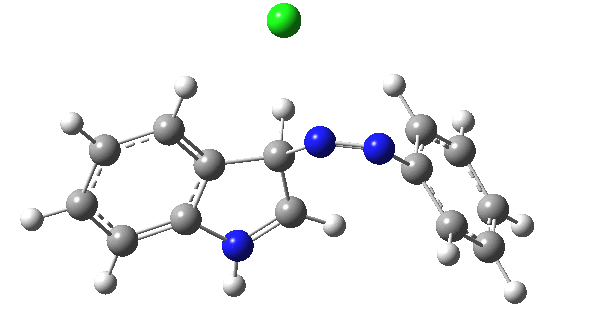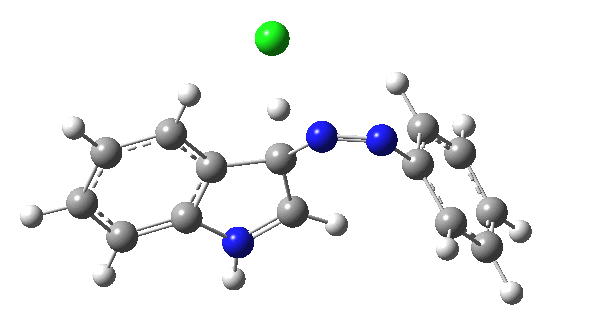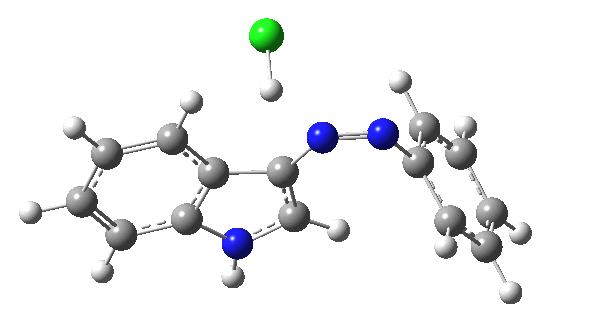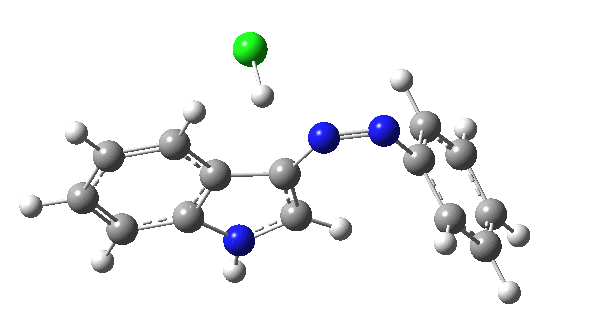
The relative free energies (kcal/mol) are shown in the table below and the following conclusions can be drawn from this computed model:

1. For R=R'=H, ΔG₂₉₈^‡ for TS1 is higher than TS2 (✔ with expt)
2. With R=t-butyl,R'=Me, ΔG₂₉₈^‡ of TS1 is 3.1 kcal/mol lower than with R=R'=H. This indicates that t-butyl and methyl groups actually activate electrophilic addition by stabiisation of the induced positive charge, and have no steric effect upon the first step (✔ with our conclusions).
3. For R= t-butyl,R'=Me, ΔG₂₉₈^‡ of TS1 is lower than TS2 (✔ with expt).
4. With R=R'= t-butyl, ΔG₂₉₈^‡ of TS2 is 4.9 kcal/mol higher than with R=R'=H and is 3.1 kcal/mol higher with R=t-butyl,R'=Me, indicating the steric effect acts on this stage.
5. The angle of approach of the diazonium electrophile is ~123-118° for R=R'=H and R=R'=t-butyl, about 30° away from a strict pseudo-axial "reactant-like" approach as implied in our sketch above (❌ with diagram above)
6. The angle of proton abstraction with the plane of the indole ring is 107° for R=R'=H and 100.3° for R=R'=t-butyl, the hydrogen being closer to pseudo-axial than equatorial, relative to the plane of the indole ring  (❌ with diagram above).
7. The position along the reaction path for proton abstraction is much later with R=R'=t-butyl (r_C-H ~1.42Å) than R=R'=H (r_C-H ~1.27Å),  (❌ with the statement above: a reactant-like transition state even for the proton expulsion step).
8. The cross-over between TS1/TS2 as the rds is in the region of the substituents R=Me,R'=t-butyl (~✔ with expt).
9. The steric interaction occurs not so much between the incoming base and the t-butyl groups, but because of enforced proximity between the t-butyl group and the diazo group induced during the proton removal stage.
10. The steric effect induced by R=t-butyl is greater than when  R'=t-butyl.
11. The Wheland intermediate is in a relatively shallow minimum.

R, R'	TS1, ΔG298‡  k1	∠ N1-C3-N2	Int ΔG298	TS2, ΔG298‡  k2	∠ N1-C3-H	ΔΔG‡ (TS2-TS1)	kH/kD (calc) [cite]10.5281/zenodo.19272[/cite],[cite]10.14469/hpc/176[/cite]
R=R'=H	21.4[cite]10.14469/ch/191705[/cite],[cite]10.14469/ch/191698[/cite]	122.9	19.6[cite]10.14469/ch/191713[/cite]	18.6[cite]10.14469/ch/191712[/cite]	107.0	-1.8	0.925 (TS1)
R=Me,R'=t-butyl	16.9[cite]10.14469/ch/191723[/cite],[cite]10.14469/ch/191719[/cite]	121.8	15.2[cite]10.14469/ch/191721[/cite]	18.4[cite]10.14469/ch/191720[/cite]	101.8	+1.5	0.900 (TS1) 6.4 (TS2)
R=t-butyl,R'=Me	18.3[cite]10.14469/ch/191722[/cite],[cite]10.14469/ch/191717[/cite]	115.2	16.0[cite]10.14469/ch/191726[/cite]	21.7[cite]10.14469/ch/191714[/cite]	100.9	+3.4	6.8 (TS2)
R=R'=t-butyl	17.8[cite]10.14469/ch/191715[/cite],[cite]10.14469/ch/191706[/cite]	117.6	17.8[cite]10.14469/ch/191709[/cite]	23.5[cite]10.14469/ch/191718[/cite]	100.4	+5.2	6.9 (TS2)

Possible errors in the model:

1. I have not included any explicit solvent water in which hydrogen bonds to the base (the chloride anion) might moderate its properties.
2. The ion-pair reactant complex between the phenyl diazonium chloride and the indole has many possible orientations, and these have not been optimised.
3. The free energies are subject to the usual errors due to the rigid-rotor approximations and other artefacts of partition functions.
4. Other DFT functionals have not been explored, nor have better basis sets.
5. This current study is confined to formation of the cis-diazo product.

But even such a model seems to reproduce much of what we learnt about diazocoupling to 2,4-substituted indoles. The calculations you see above took about a week to set up and complete; the original experimental work took (in real-time) ~150 weeks (interleaved with two other mechanistic studies). Also efficient implementation of the quantum theories, together with the computer resources to evaluate the molecular energies and geometries, was almost entirely lacking in 1972 and this has probably only become a realistic project in the last five years or so. So that 43 year wait to finish what I started seems not unreasonable. Nowadays of course, combining experimental kinetic measurements with computational models very often goes hand in hand. It is also worth speculating about the wealth of mechanistic data garnered during the heyday of physical organic chemistry during  the period ~1940-1980. The experiments were not then informed by feedback from computational modelling. However, it seems unlikely that very many of these mechanistic studies will ever be retrospectively augmented with computed models; the funding for the resources to do so is unlikely to ever be seen as a priority.

---

^‡A little more complex than the scheme above, since the reaction also exhibits dependency on acid concentration. Nowadays, there are a number of computer programs available for analysing such complex kinetics, but in 1972 I had to write my own non-linear least squares fitting analysis of the steady state equation to the measured rates[cite]10.5281/zenodo.18777[/cite] This replaced the use of graph paper to analyse (of necessity much simpler) rate equations. I note that mentions of non-linear least squares methods in kinetic analyses start around 1986[cite]10.1021/j100281a038[/cite] Even by 1992, the topic was considered novel enough to warrant a publication[cite]10.1002/aic.690380419[/cite]

^†The related diazo coupling to activated aryls such as phenol or aniline shows a mechanistic cross-over between an entirely synchronous path in which no Wheland intermediate is involved (e.g. phenol)[cite]10.14469/ch/191700[/cite] to one where the intermediate does form (e.g. aniline).[cite]10.14469/ch/191699[/cite] Diazo coupling to e.g. benzofuran rather than indole by the way is also stepwise, but via a very shallow Wheland intermediate[cite]10.14469/ch/191730[/cite] and with a higher barrier than indole, making it a very slow reaction.

---

Acknowledgments

This post has been cross-posted in PDF format at Authorea.

Tags: Butyl, chemical reactions, Indole, Kinetic isotope effect, Organic chemistry, Physical organic chemistry, potential energy surfaces, relative energy

This entry was posted on Thursday, December 24th, 2015 at 7:36 pm and is filed under Historical, Interesting chemistry, reaction mechanism. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.