The period 1951–1954 was a golden one for structural chemistry; proteins, DNA, Ferrocene (1952) and the one I discuss here, a bonding model for Zeise’s salt (3).
In “A review of π Complex Theory”, Bull. Soc. Chim. Fr., 1951, 1 8 , C79 (it is not online) M. J. S. Dewar sets out his theory of the role of π-complexes in (mostly) organic chemistry. The paper derives from an international colloquium held in Montpellier, in which audience responses to the presentation are included as an annex to the article itself. It is as a footnoted response (to P. Bartlett) that Dewar presents his theory of the alkene-metal π-complex, of which the best known example is Zeise’s salt (3).

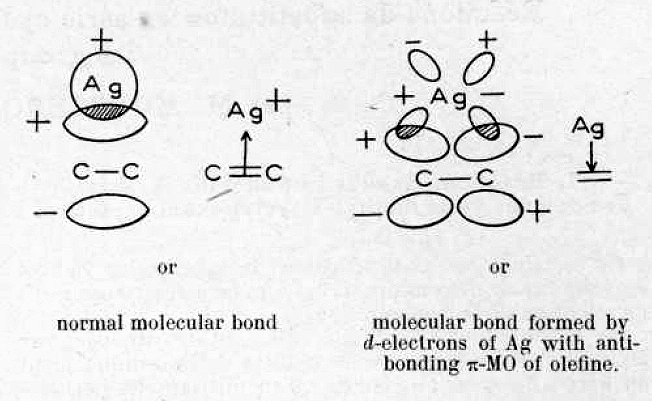
This diagram illustrates the binding of a silver cation Ag+ to ethene (1). Dewar uses group theory to show how the molecular orbitals from ethene can be combined with the atomic orbitals on the metal. Two filled and two empty orbitals combine to give two new combinations, with a total occupancy of four electrons defining the interaction between alkene and metal. Dewar regards this four-electron-three-centre interaction as distinctive from simply the formation of two single metal-C bonds (a metallacyclopropane).
Zeise’s salt itself derives from Pt2+ by addition of three chloride anions to give PtCl3–. To compare this with Dewar’s Ag+ example, I use here just the naked metal cations 1-2.‡ I went about this analysis as follows:
- I did ωB97XD/Dev2-SVP calculations, optimising the geometry into C2v symmetry.
- The electronic configuration of Ag+ is [Kr].4d10.5s0 and Pt2+ is [Xe].4f14.5d8.6s0.
- The two metals therefore do differ; Ag+ can only accept electrons into a 5s atomic orbital (AO), whilst the Pt2+ can accept electrons into either the 6s or the empty 5d AO.
- The molecular orbitals identified for discussion here at 17, 13 and 11 (this is a pseudopotential calculation) of which 17 is doubly occupied for Ag+ and unoccupied for Pt2+. Why three when Dewar’s analysis above describes only two? All (might) become clear shortly!
- Firstly, I start with the “back-bonding” orbital as shown on the right in Dewar’s diagram. This is the interaction of the filled metal dxz orbital with the alkene π* empty anti-bonding orbital and the combination emerges as orbital 13 of the three considered here. It is antisymmetric with respect to rotation about the axis of symmetry and one of the two planes of symmetry, and is given the label (irreducible representation) B1. Map Dewar’s “-“ sign to blue and “+” sign to purple to match them up. But also notice that the Pt orbital is rather more anti-bonding in the C-C region than Ag analogue. The C-C computed length (1.423Å) is indeed longer than that for the Ag complex (1.363Å, click on the images below to see a rotatable model of these orbitals). You will also notice that this orbital is “contaminated” with contributions from the C-H bonds; no longer are the π- and σ- electrons orthogonal as they are in ethene itself. This mixing of components from other parts of the molecules is what makes a clear-cut analysis of such systems trickier than you would infer by looking at Dewar’s diagram above! This also happens from the ligands on the metal (Cl in Zeise’s salt for example).
Ag Pt 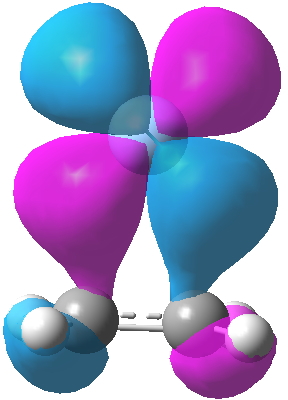
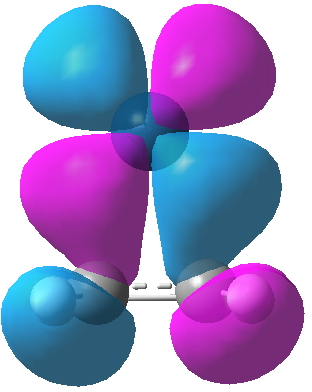
- Let us now go hunting from the second of Dewar’s orbitals, which he describes as the interaction between the filled alkene π-MO and an empty Ag s-AO. Orbital 17 closely resembles Dewar’s sketch on the left, although additional lobes can be seen. It is symmetric with respect to all three elements of symmetry (axis and two planes) and hence is labelled A1. Where Dewar writes that the two molecular bonds are distinct, he means that they have different symmetries and hence cannot interact with each other (they are orthogonal). But hang on; although this orbital is doubly occupied for Ag, it is unoccupied for Pt! So does that mean that Dewar’s argument cannot hold for Zeise’s salt itself (the bonding in this molecule is often referred to as the Dewar-Chatt-Duncanson model[1]). No. It turns out that for Ag, the alkene π-MO is interacting not with a pure unhybridised Ag s-AO, but with an s+dz2 hybrid (albeit with rather more s and rather less dz2). This creates two modified hybrid AOs, one of which interacts with the alkene π-MO to give orbital 17. This is what those extra lobes are about, the contribution from the 4dz2 AO on Ag. Because this combination on Pt is empty, the Ag complex has a shorter C-C bond than Pt.
Ag Pt 

- Well, Pt still needs explaining, since we have only found one of Dewar’s two interactions. I mentioned that s+dz2 hybrids could be created, and here the second of these interacts with the bonding alkene π-MO to give another A1 instance 11, again with the same symmetry properties with respect to the three elements of symmetry present (but this time with rather more dz2 than s). It is this orbital which is now occupied for Pt.
Ag Pt 

The famous Dewar π-complex model of alkene-metal interaction as applied to the Ag+ cation describes one “normal molecular bond” and a second bond “opposite in direction to the first”, what we now call a back-bond. What has emerged however is that two “normal molecular bonds” can be identified for Ag+ based purely on their symmetry but only one for Pt2+ (which of course has two valence electrons less) and both exhibit one back-bond. The diagram above must absorb a further pair of electrons from a formally non-bonding filled dz2 orbital, whilst recognising that hybridisation may allow it too to take on some bonding role.
You might ask what the missing orbitals 12, 14-16 are? Well, formally they derive from the other occupied four metal d-orbitals, but in fact mixed heavily with the C-H bonds of the ethene. I have to conclude that a molecular orbital analysis of e.g. Zeise’s salt (with additional orbital mixing from the three chlorides) ends up being pretty complex! But despite this complexity, Dewar’s original hypothesis, produced in response to a question from the audience, certainly started something. It is worth reminding that the 1952 Nobel-prize winning suggestion for the structure of Ferrocene[2] includes no group theoretical orbital analysis of the bonding on a par with Dewar’s 1951 insights.
‡ In fact, the MOs turn out to be pretty sensitive to the ligands surrounding the metal, and so those presented here for the naked cations will differ from those for “real molecules” such as Zeise’s salt.
References
- J. Chatt, and L.A. Duncanson, "586. Olefin co-ordination compounds. Part III. Infra-red spectra and structure: attempted preparation of acetylene complexes", Journal of the Chemical Society (Resumed), pp. 2939, 1953. https://doi.org/10.1039/jr9530002939
- G. Wilkinson, M. Rosenblum, M.C. Whiting, and R.B. Woodward, "THE STRUCTURE OF IRON BIS-CYCLOPENTADIENYL", Journal of the American Chemical Society, vol. 74, pp. 2125-2126, 1952. https://doi.org/10.1021/ja01128a527
Tags: alkene-metal interaction, alkene-metal π-complex, cation Ag, Dewar, Dewar's Ag, Historical, metal, metal d-orbitals, naked metal cations, ZTE C79 Cellular Phone
[…] Chemistry with a twist « The π-complex theory of metal-alkene compounds. […]