Michael Dewar[1] famously implicated a so-called π-complex in the benzidine rearrangement, back in the days when quantum mechanical calculations could not yet provide a quantitatively accurate reality check. Because this π-complex actually remains a relatively unusual species to encounter in day-to-day chemistry, I thought I would try to show in a simple way how it forms.
I am actually illustrating it with the benzidine rearrangement of monoprotonated PhNHOPh, which I dealt with in the previous post, if only because the energy of this π-complex relative to monoprotonated PhNHOPh is amazingly low (in other words, it is not one of these high energy molecules which only exist in the virtual world of computational modelling). The mechanism can be conceptually broken down to considering how the N-O bond can be cleaved in one of three ways. Route A is the homolytic route to give a 4-biradical (in one of the possible resonance forms), which of course can couple to form a 4,4′-biphenyl. Route B is a heterolytic route in which the two electrons from the N-O σ-bond are retained by 1, whilst for route C this electron pair is retained by 4.
These two fragments can then interact in several ways to form the π-complex. Here I will illustrate just the two closed shell options (B/C), whilst recognising that there may also be contribution from the open shell biradical (in water as solvent, the two ionic configurations are clearly going to be stabilised by solvation and so may contribute relatively more than the non-polar radical-pair ).
- Route B (green), overlapping the HOMO of 1 with the LUMO of 2 to create a new π-MO to be occupied by the two electrons extracted from the N-O σ-bond (a similar promotion of a σ- to a π-pair was noted in this post).
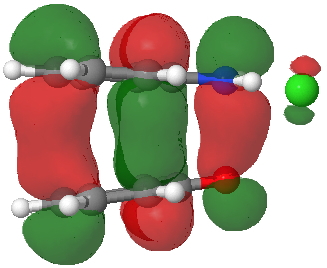
- Route C (red), overlapping the HOMO of 4 with the LUMO of 3 to achieve the same result.
| Route B | |
|---|---|
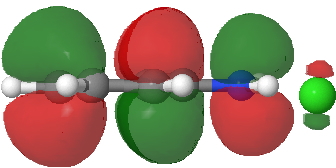 LUMO of 2. Click for 3D. |
 HOMO for π-complex. Click for 3D. |
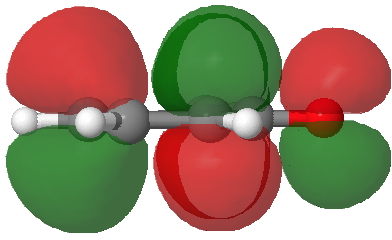 HOMO of 1. Click for 3D. |
|
| Route C | |
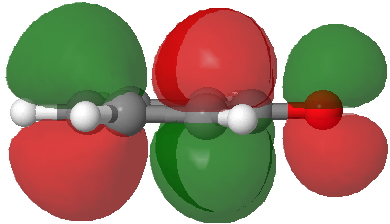 LUMO of 3. Click for 3D. |
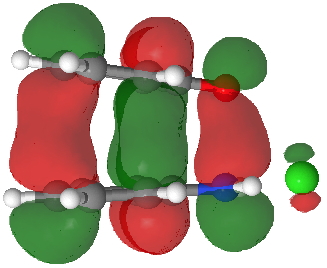 HOMO for π-complex. Click for 3D. |
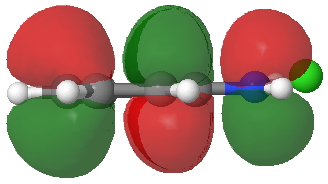 HOMO of 4. Click for 3D. |
|
The relative weight of these two combinations is largely determined by the difference in energies between the two HOMO/LUMO pairs and their overlap. ΔE is different for the two combinations, being 0.021 Hartree (route B) and 0.091 (route C), with lower being better.
The overlap of the HOMO/LUMO (in either orbital combination) is almost perfect for the face-to-face π-stacking of the complex. Note that this π-π-stacked arrangement in effect returns some electrons to the N-O region, in what is now called σ-π conjugation, and which used to be called hyperconjugation (it also resembles the conjugation of a Si-C bond with a phenyl ring in the Wheland intermediate).
Acknowledgments
This post has been cross-posted in PDF format at Authorea.
References
- M. Dewar, and H. McNicoll, "Mechanism of the benzidine rearrangement", Tetrahedron Letters, vol. 1, pp. 22-23, 1959. http://dx.doi.org/10.1016/S0040-4039(01)82765-9
Tags: energy, high energy molecules, Interesting chemistry, Michael Dewar, Reaction Mechanism
[…] Chemistry with a twist « The π-complex in the benzidine rearrangement: a molecular orbital analysis. […]
[…] In an earlier post, I had shown how an in-phase combination of the HOMO of the anion 1 with the LUMO of the cation 2 led to an occupied molecular orbital for the complex (below, left). An out-of-phase combination of these two gives instead the LUMO of the π-complex (below, right). It might seem as if a pair of electrons would to occupy the first of these, and indeed a wavefunction constructed on this basis (using this occupancy as the single reference; indeed only state) resulted in the conclusion that the complex was aromatic. The diatropicity (~magnetic aromaticity) was strongest in region between the two stacked rings, and the individual rings themselves had lost their local aromaticity. One might then infer that a wavefunction constructed by populating the LUMO below would in fact rearrange the aromaticity, returning this property back to the two individual rings. There would in fact be apparently nothing to keep the rings stacked, and so in the limit this wavefunction would correspond to a biradical. […]