This reaction looks simple but is deceptively complex. To recapitulate: tolyl thiolate (X=Na) reacts with the dichlorobutenone to give two substitution products in a 81:19 ratio, a result that Singleton and Bogle argue arises from a statistical distribution of dynamic trajectories bifurcating out of a single transition state favouring 2 over 3. On the grounds (presumably) that the presence of both the cation X (=Na+) and H-bonded solvent (ethanol) are uninfluential, neither species was explicitly included in the transition state model used to derive the dynamics. I speculated whether in fact the spatial distribution of counterions and solvent (set up by explicit hydrogen bonds and O…Na+ interactions) might in fact be perturbed from un-influential randomness by co-ordination to the carbonyl group present in the system. I also raised the issue of what the origin of the electronic effects leading to the major product might be.
In this post I try to delve deeper into both these issues. In the earlier model, I focused on possible coordination models around that carbonyl, using two Na+ cations (on the premise that such coordination has precedent in crystal structures). This model did (correctly) predict this major product, and we are now discussing what the origins of the minor product may be (it is a measure of how far computational modelling has come that we are nowadays increasingly concerned with these minor outcomes). Here I move to a more stochiometric model using just one Na+ assisted with four solvent molecules (modelled here with just water). This results in an overall charge of zero on the whole system, which avoids having to create what could be regarded as artificially charged models resulting from omission of the counterion. Three possible arrangements of these additional units are shown below, selected for the following reasons:
- (a) was set up to explore whether the orientation of the tolyl thiolate ring might be determined by either π-facial hydrogen bonds to the solvent, or a π-facial interaction with the Na+.
- (b) was set up to explore if moving the Na+ closer to the thiolate would influence which of the two chlorines (red or green) would be eventually ejected.
- (c) was set up to explore whether the orientation of the carbonyl group might be influencing the outcome, based on differing stereoelectronic interactions between the two C-Cl bonds and either the C-C(C=O) unit or the alternative C-H bond.
- (d) whether replacing the C-H bond in (c) with a C-F bond results in a different interaction with the two C-Cl bonds.
We might ask why stop at just these four? Surely one should sample all reasonable explicit models that might have a significant Boltzmann population in the real reaction? That is certainly desirable (but a much larger computational project); here I am just using these models for the purpose of understanding a little better what might be going on.
Model (a)
This is optimised using the same level as before (B3LYP/6-31+G(d,p)/SCRF=ethanol) and reveals that the Na+ cation ends up with coordination just from solvent, and not from the aryl face. The chlorine labeled green in the diagram above ends up being evicted, and its trajectory then leads it (slowly) towards the Na+ cation in a reaction that is fully concerted (no enolate anion intermediates along the route).
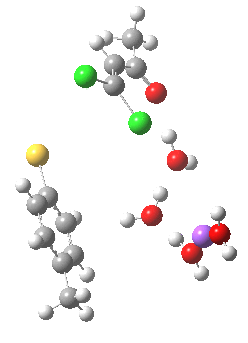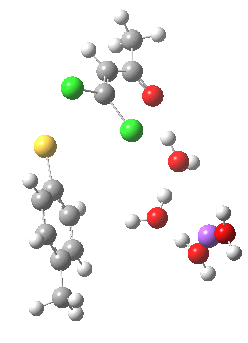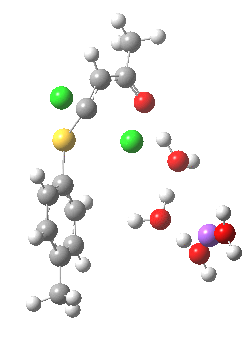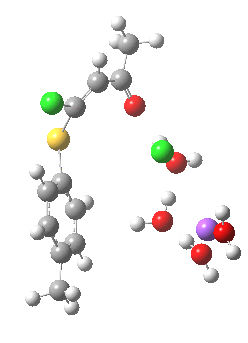
The IRC for this model has the following intriguing features:
- At an IRC = 0.0 (the transition state), the lengths of the C-Cl bond for the atom labelled red is 1.84Å and green is 1.817Å. This situation persists until around IRC = -1 (1.926Å and 1.915Å). In other words, the longer of the two C-Cl bonds is NOT the one that is about to be ejected. But here is the even odder thing. The Wiberg bond order index of these two C-Cl bonds is respectively 0.932 and 0.916 at this stage. Here we see the longer bond having also the larger bond order, and so the bond order (but not the bond length) turns out to be the more reliable indicator of which bond is about to break totally. The NBO E(2) term shows that the C-Cl(green) bond has a significant interaction with the antiperiplanar C-H bond (also shown in green) of 4.9 kcal/mol, compared with the C-C (red) σ-bond which has a lower E(2) term for interaction with the antiperiplanar C-Cl(red) bond of 2.1. [Added in proof: Donation from the C-Cl bonds into the C-S σ* bond is also greater for C-Cl(green, 81 kcal/mol) than C-Cl(red, 25 kcal/mol)]**. These effects all conspire to weaken the C-Cl(green) bond more than the C-Cl(red) alternative.
- Only at IRC -1.5 (well past the transition state) do the two C-Cl bond lengths become equal (~1.95Å). So initially at least, BOTH C-Cl bonds start to cleave, but then stereoelectronic effects take over and a discrimination in favour of the green C-Cl bond wins out over the red.
- By IRC -4, the C-Cl(red) bond has reversed its elongation, and has contracted back down to 1.86Å, whilst the C-Cl(green) has continued to extend to 2.76Å.
- By IRC -8, the formation of NaCl is complete.
- Thus we can say that the major product of this reaction results from stereoelectronic control discriminating between the two chlorine atoms.
- We might also observe that because post-transition state the two C-Cl bonds continue to elongate (before one bond continues on its way and the other backtracks), the dynamics of what goes on (via coupling with rotational and other vibrational modes) could easily account for the (minor) outcome, as indeed Singleton and Bogle argued.
The next task is to see how stable the above effects are to the disposition of the Na+ and solvent molecules. Model (b) shows the same behaviour; the chlorine atom is evicted via stereoelectronic control, rather than simply heading off towards the Na+ atom (i.e. electrostatic control).
Model (c) also demonstrates how the stereoelectronic alignments dominate over stabilisation of the forming chloride anion. This time, the chloride is evicted into a region not occupied by either solvent molecules or the Na+ ion, the charge being stabilised only by the continuum solvent field.
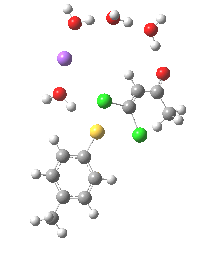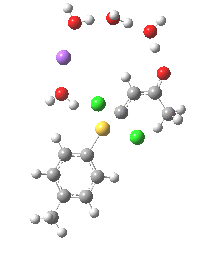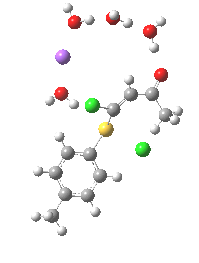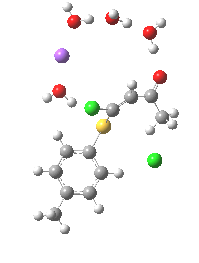
Model (c) was also subjected to a robustness test of the actual wavefunction. The original method was based on B3LYP/6-31+G(d,p)/SCRF=ethanol. Accordingly, (c) was re-computed using ωB97XD/6-311+G(d,p)/SCRF=ethanol. The DFT functional is a more modern one that includes the effects of dispersion attractions, and the basis set is of triple rather than double-ζ quality. The essential features are unchanged.
Model (d) tests whether perturbing the electronic environment has more effect than changing the explicit surroundings.
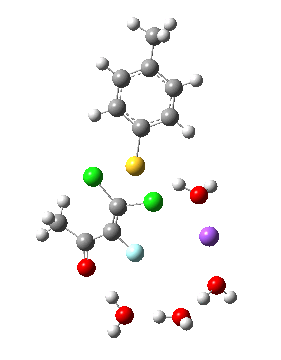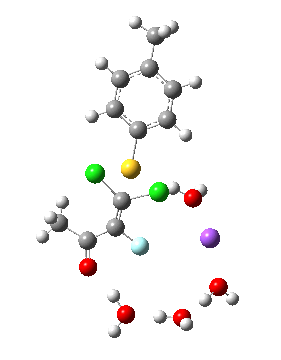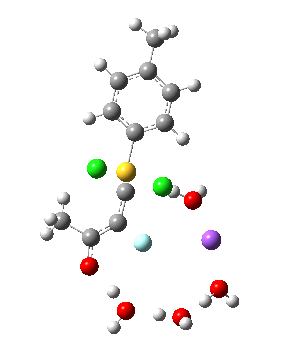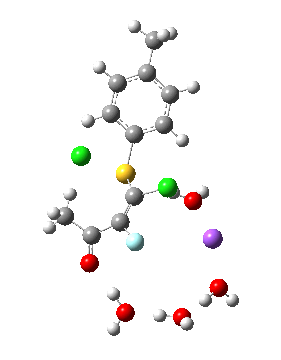
- It turns out that this is even more complex stereoelectronically. Observe how the bond to the (cyan coloured) fluorine atom elongates before shortening again as the anti-periplanar C-Cl bond breaks. The length starts off as 1.41, lengthens to 1.45 (at IRC +2.6) before ending up as 1.414Å, again the result of stereoelectronic effects.
- A second noteworthy feature is that at IRC +2.6, the gradients (almost but not quite) drop to zero. At this stage, both C-Cl bonds AND the C-F bond are approximately at their maximum length, and this almost constitutes a discrete intermediate along the pathway.
- The feature in the gradients at IRC +5 represents the eviction of the chloride.
I will conclude by summarising the above. The formation of the dominant product 2 seems to be the result of stereoelectronic control at the transition state. This outcome seems to be pretty robust to the transition state model constructed, namely whether one (or two) Na+ counter-ions are included in the model, and indeed their position, as well as the inclusion of up to four explicit solvent molecules. This robustness even extends to an electronic perturbation resulting from replacing a C-H bond by a C-F bond. Thus constructing a selection of physically realistic models with neutral charge and solvent has not resulted in locating an explicit transition state which (in terms of its free energy) might account for the formation of the minor product 3.
Another test which might be envisaged would be to take e.g. model (a) and subject it to molecular dynamics to show that the outcome, in which ~20% of the trajectories lead to 3, is itself robust towards addition of counter-ion and solvent to the original model.
These values do seem to be very basis set dependent. Thus using B3LYP/6-311+G(d,p), the σC-Cl(green) to σ*C-S value is 58 and σC-Cl(red) to σ*C-S is 18. The trend however occurs across basis sets.
Tags: free energy, IRC, minor product, Reaction Mechanism, substitution products
I noted in a footnote above that the NBO E(2) energies seem sensitive to the basis set used. I also noted that if ωB97XD/6-311+G(d,p)/SCRF=ethanol replaces B3LYP/6-31+G(d,p)/SCRF=ethanol for model (c) the essential features were unchanged.


But the quantatitive aspects do look different:
For example, the gradient norm at IRC +2 takes a different form for B3LYP/6-31+G(d,p) compared with ωB97XD/6-311+G(d,p). The derivative of these gradients also shows differences. This suggests that the latter is perhaps closer to forming a transient intermediate along the path than the former and also hints that the forces acting on the atoms along this path may in turn be quite sensitive to the method used. Another smaller, but intriguing difference is that the gradients for B3LYP/6-31+G(d,p) are quite “bumpy”, whereas ωB97XD/6-311+G(d,p) is much smoother.
We may speculate whether these quantitative differences will impact upon the molecular dynamics calculated using either of these methods, or whether the dynamics turns out to be quite robust to basis set and DFT method.
Oh, you might ask why I use ωB97XD in preference to B3LYP. Well, calibrations on relative energies of a collection of small molecules compared to CCSD(T) calculations suggest that the former matches much better than the latter. For systems where weak interactions between assemblies of molecules matter, ωB97XD does seem to come up with quite realistic simulations. And I believe that dynamics simulations can be sensitive to the potential used.
PS: For proper comparison, the below is the IRC gradient norm computed at ωB97XD/6-31+G(d,p) and ωB97XD/6-311+G(d,p) (no additional counterion or solvent). This shows the the big difference is the functional and not the quality of the basis set, or indeed the presence of counter-ion and solvent.


[…] find in the research literature and textbooks; the counter-ion (Y=Na+) is also included so as to create a neutral system overall. The method is the usual […]
[…] transition state for each product in a reaction. But one should note that there are increasing claims for reactions whose outcome is determined not by an explicit transition state for each reaction pathway, but […]