In the preceding post, I described a fascinating experiment and calculation by Bogle and Singleton, in which the trajectory distribution of molecules emerging from a single transition state was used to rationalise the formation of two isomeric products 2 and 3. In the present post, I explore possible consequences of including a sodium cation (X=Na+ below) in the computational model.
Sitting down to construct such a model, one is immediately faced with important decisions. Na+ comes with baggage, namely groupies in the form of solvent molecules and ionic bonding. The latter means less certainty regarding where to place the ion (covalent bonds have that nice attribute that their orientation and length is pretty predictable most of the time). I decided to construct the model shown below, using not one Na+ but two (such structures are known from the Cambridge crystal data base), the second Na+ being charge balanced by hydroxide anion.
The resulting transition state (B3LYP/6-31+G(d,p)/CPCM=ethanol) is shown below, and the free energy activation barrier, ΔG† is 11.7 kcal/mol, well down on the value obtained using X=H+, and entirely reasonable for a reaction occurring at room temperature. This suggests that the model is not unreasonable (but of course does not prove it is the best).
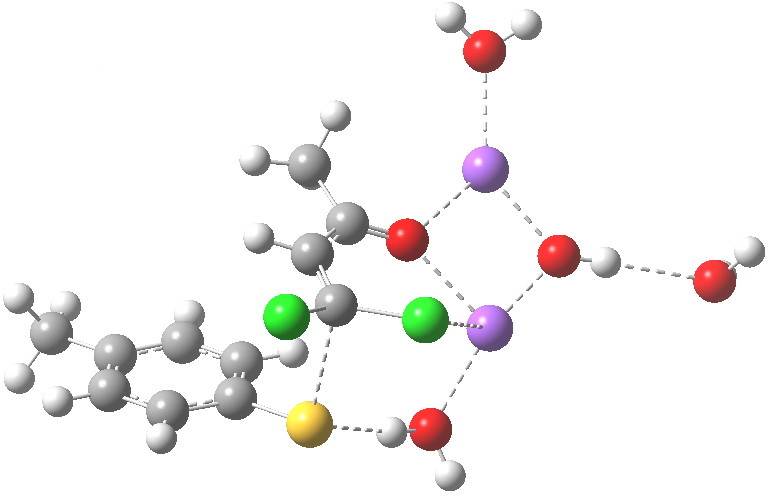
The geometry of this transition state is significant. Of the two C-Cl bond lengths, the shorter (click the image above to inspect the model) is the one cis to the carbonyl (subsequent elimination of which would result in formation of the major product 2). But an IRC reveals what happens next. Recollect that when X=H+ a tetrahedral intermediate is formed that then collapses with elimination of H3O+Cl–. This time, no intermediate is seen on the IRC, and the requisite C-Cl bond is broken to form 2 in a concerted (but very asynchronous) manner, and in the manner reported by Bogle and Singleton for a model without counterion and explicit solvent.
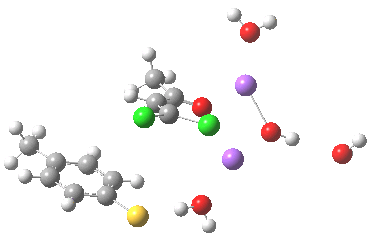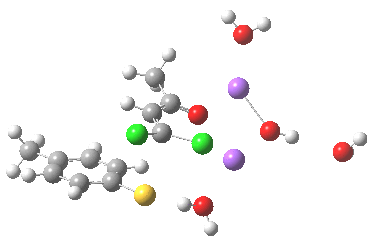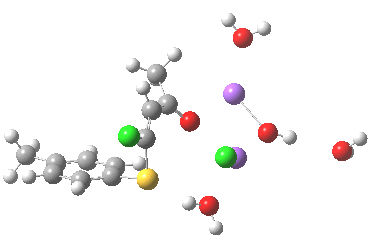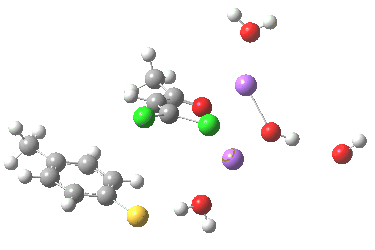
Notice how preparation for eviction of the C-Cl bond only starts after the transition state is passed. The forces on the departing chloride start to grow after the dihedral angle of the Ar-S-C-Cl system has become antiperiplanar (IRC -3), resulting in the anion shooting out towards one of the two Na+ cations to form solvated NaCl.
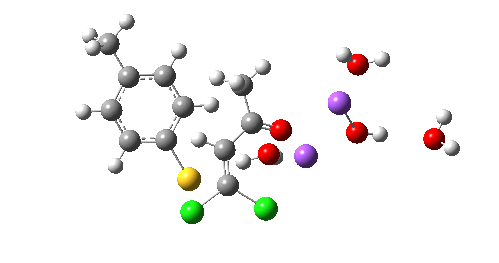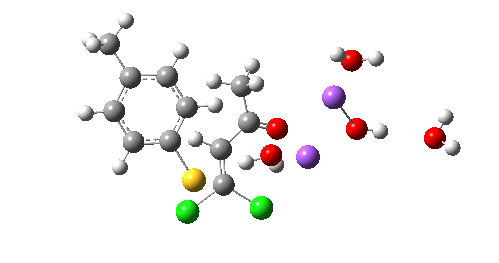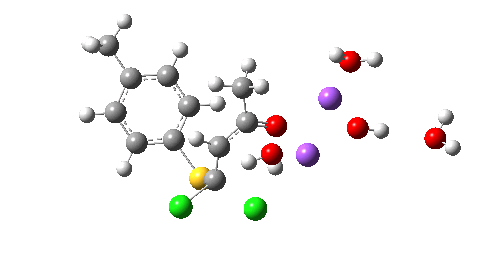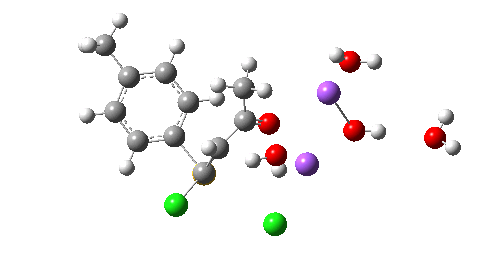
So we now have a rather more complete model. But is it yet complete enough? How would one go about evicting the other chloride, resulting in formation of 3? I think it is fairly clear that the model will have to be enlarged yet again, this time to include at least one more Na+ located on the other side of the carbonyl, and ready to receive the anion. Possibly at least another two water molecules and one hydroxide anion would be required to surround this cation. Clearly, such a model would have grown substantially compared to the original one (Occam might not be happy), and that we are gradually edging towards having two quite separate transition state models to account for each of 2 and 3. At this stage, it would be interesting to apply Bogle and Singleton‘s direct dynamics model to try to establish if each transition state leads to only one product, or whether either of these transition states could result in cross-over to the other product.
I have no feel for whether the transition state presented here can be treated using direct dynamics; if it could, that would indeed be an interesting simulation.
Tags: Cambridge, isomeric products, Reaction Mechanism, simulation
Nice post, but I’m puzzled. Why did you choose to put two Na+ ions? Why wasn’t one Na+ enough? Were you trying to keep some coordination number?
Excellent and perceptive question. If you look back to my first attempt, I was using X=H(+) as a model, with an intervening water molecule. In fact, a proton transfers from the S(-) to the water, and then a different proton jumps from that water molecule on to the carbonyl oxygen. So I needed two protons to allow the chain to complete. The next step was to change X=H(+) to X=Na(+), and so I decided to simply turn these two protons into two sodium cations. Into the computer this went, but the system reorganised itself. The two sodium cations moved, and both attached themselves to the carbonyl, leading to a quite different structure from the original proton one. I decided to keep it anyway.
Of course, now that one has learnt something, one could try trimming this model down to just one Na and seeing what happens (one could probably also trim off one water as well).
This now raises a more subtle problem. At what point does one decide that the model is trimmed down to its essential features, and no more? My hypothesis I am testing here is that trimming it down to remove the 2Na(+) and the water molecules entirely would reduce down to Bogle and Singleton’s original model, which (so I am suggesting) might (only might) be a step too far in simplification. To put it another way, if the model with two Na(+) and water/hydroxide results in the same dynamic behaviour as the original model, then the larger more complex model explains nothing new, and so is not needed (Occam). However, if the larger model does not give the same dynamic behaviour as the one without the extra ingredient, them perhaps this larger model is a better description after all.
This problem always raises it head when dealing with explicit solvent molecules. But in a sense, it is similar to another question; how large a basis set should one use to describe the wavefunction? The CBS (complete basis set) limit suggests one will approach better solutions as one does. Perhaps the same applies to solvent molecules (and the law of diminishing return).
A postscript. I am reminded, in the above discussion of Kaluza-Klein theory. This dates back to 1921, when Kaluza extended Einstein’s space-time to five dimensions, and found that the general theory of relativity also could be made to incorporate Maxwell’s equations for an electromagnetic field. A single set of equations which described two fundamental fields. As I understand it, this apparent elegance was not met with great enthusiasm. It predicted nothing new over the individual field theories, no new experiment to test new predictions, just mathematical elegance. Of course, Paul Dirac then based his life on (and won the Nobel prize for) mathematical elegance in quantum mechanics. But his equations did manage to predict the positron!
Another postscript. Now I am really going well beyond what I truly understand. But Dirac formulated a description of the energy of an electron in its own field. I am intrigued by the SM Higgs Boson, and the difficulty of understanding how it gives mass to itself! Enough!!
Thanks for the enlightening explanation.
Regarding the (over)simplification of the models, I tend to approach the other way around, making the model more complex little by little until I either learn nothing new (sometimes) or until the model becomes so large that I cannot calculate it with my computer resources (most of the time).
Really, any geometry proposed is a hypothesis, and the computation is our way of testing for its “validity”. So, I guess one can always analyze the diverse hypotheses and decide which ones do not represent anything new. Of course, computation can always reorganize the system in an unforseen hypothesis, in a similar way to an experiment that yields an unforseen product.
Finally, I think one should not abuse Occam by discarding a hypothesis that “does not add anything new”. I prefer to say that several hypotheses are undistinguishable by the current experimental knowledge, and I may even try to suggest an experiment that could distinguish among them.
Thank you again for keeping this blog.
Indeed, the question of “trimming the model” is important. Bogle and Singleton recognize it and question their own model by making the following statement: “The reliability of any simple calculational model, by itself, for a polar reaction in solution is intrinsically questionable”. Nevertheless, they obtained a remarkable agreement between experimental (81:19) ratio of products and 84(+/-5) percentage of the main product obtained from the trajectories. Based on the almost perfect agreement between experiment and theory, I think that Occam would be happy with the simple cation-free model (even though I do find the dance of cations along the IRC trajectories both elegant and though-provoking).
[…] an ionic mechanism. And if one does not forget the counter-ions in all of this (see my post on not forgetting them!), it is an ion-pair mechanism. But in relatively non-polar media, need ion-pairs form? A little […]
Xavier Bogle and I greatly appreciate the interest in our work. We disagree with the blog posts on multiple levels, that is, with the particulars of the models presented, the theme of the posts, and the approach to science being undertaken. However, we are happy to discuss our work and feel that this particular discussion may be broadly educational.
I started to write a much longer discussion but at the end of a couple of pages I realized that I was less than half done with a post that perhaps no one would read. So let me outline my points and I can elaborate as desired.
1. The sodium ion is probably not associated, but to the degree that it is it makes no experimental difference.
2. Even if it were involved, simply throwing in a sodium ion and finding a saddle point would hardly constitute the theme of modeling a complete system. Polar reactions in solution occur by ensembles of transition states.
3. The blog models that include zero sodium ions, or two sodium ions, or next, three plus a hydroxide ion, are, well, our polite word is “nonphysical.” Aside from the particular models being inconsistent with experimental observations, dancing motions of protons or sodium ions are always sexy to the eye but real reactions almost never happen this way.
4. Computational studies by any approach provide _models_ of mechanisms, and these models only become science only when they make predictions of experimental observations. Until they do so, and their predictions are found to reasonably fit with experiment, they haven’t left the starting gate. I would disagree with considering models that fit with experimental observations and those that have not been shown to fit, or are in fact inconsistent, on an equal footing, in the manner of a news story.
Thanks Dan. Your thoughtful response is much appreciated. Like yourself, I dare say I could also write a few pages, and so will also try to keep it short.
1. I would be interested in how you know the Na is not associated? I dare say at infinite dilution, but even if surrounded by solvent it seems likely that a Na(+) would be in proximity (let us not use the loaded word “associated”). Might that not affect vibrations/rotations?
2. I do not think I was claiming to have myself modelled a complete system. Indeed, my posts show, I hope, my model evolving. In a sense, it was a devil’s advocate position. I was asking “show me that the Na and explicit solvent are not important”; I wanted rather more than just “the right answer is obtained with them missing”. I am not yet convinced they are not important, although you probably have lots of evidence you have not presented here.
3. My point again was that a complete absence of both Na(+) and hydrogen bonding solvent could itself be regarded as “nonphysical”, the elephants in the room if you like. I do indeed sometimes ask students “can you put 100g of just chloride anions into a reaction flask?”
4. In a blog there is an opportunity to show science “behind the scenes”. In this case, you can see me asking a question “what might be missing?”, adding it into to a first attempt at a model (using H(+), trying a second model with two Na(+), and suggesting at the end that a further model appropriate for exploring the formation of the second product is needed using the classical transition state approach.
Indeed the reader can also see you, I (and others) participating in a friendly discussion to explore some fascinating themes.
[…] neither species was explicitly included in the transition state model used to derive the dynamics. I speculated whether in fact the spatial distribution of counterions and solvent (set up by explicit hydrogen […]