Astronomers who discover an asteroid get to name it, mathematicians have theorems named after them. Synthetic chemists get to name molecules (Hector’s base and Meldrum’s acid spring to mind) and reactions between them. What do computational chemists get to name? Transition states! One of the most famous of recent years is the Houk-List.
In the last 12 years or so, the area of enantioselective organocatalysis has blossomed, and an important example involves the asymmetric amino acid (S)-proline (below, shown in green). As its enamine derivative (below, shown in blue), it can catalyse the aldol condensation with an aldehyde or ketone to form two new adjacent stereogenic centres resulting from C-C bond formation (shown below as (R) and (S) as attached to the carbons connected to the red bond).
The Houk-List transition state was located for this reaction, and as a useful model for rationalising the stereospecificity of this reaction it has become justly famous (although to be fair, other models have also been proposed). The challenge is to identify the factors selecting for just one stereoisomer (S,R in this case) over the other three (a similar challenge is described in this post for the heterotactic polymerisation of lactide). Houk, List and co-workers constructed their model (the example shown below is for R=isopropyl) as follows.
- They employed a B3LYP/6-31G(d) density functional model.
- The geometry of the transition state was located for all four diastereomeric transition states using this method. Importantly, this geometry was for the gas phase, which provided a value for ΔG298†.
- These free energies were then corrected for the (relative) solvation energies of the four transition states. This was essential, since in the mechanism shown above, a neutral reactant gives a zwitterionic product, via a partially ionic transition state (indeed, the dipole moment of these transition states is around 10D).
- The resultant Houk-List model then predicted that of the four isomeric transition states, the lowest was (as shown above) the (S,R) diastereomer.
- This particular transition state geometry has an interesting feature involving a 9-membered ring, large enough to accommodate a linear proton transfer without strain, by virtue of a trans double bond motif (the C=N bond). The (S,S) and (R,S) isomers have a cis motif instead at this location.
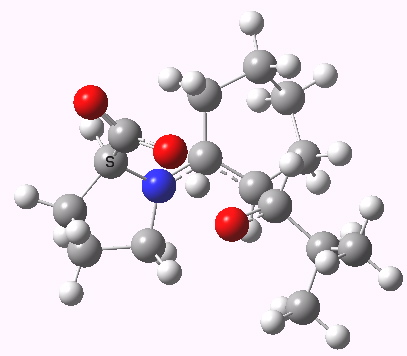
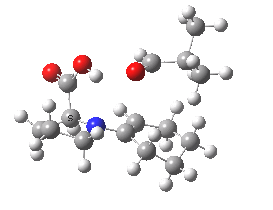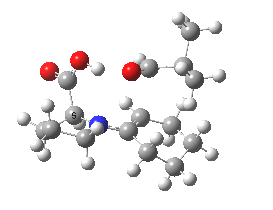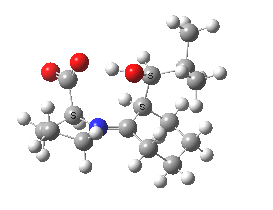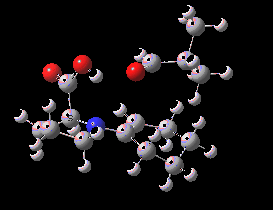
Houk-List transition state. Original geometry.
Well, this transition state is now nine years old. Unlike asteroids, or mathematical theorems, or indeed molecules and their reactions, a transition state is a slightly more ephemeral object. Its features and properties do rather depend on the particular quantum model used to construct it. There is one feature of the model, necessary in 2003, but no longer so in 2012. This was the use of a gas-phase optimised geometry, augmented at that geometry with a so-called single-point solvation energy correction. Nowadays, the solvation correction is included in the energy used in the geometry optimisation, which now properly reflects the effect of the solvation. Re-optimisation with this inclusion, at the ωB97XD/6-311G(d,p)/SCRF=dmso level thus updates the original Houk-List geometry.
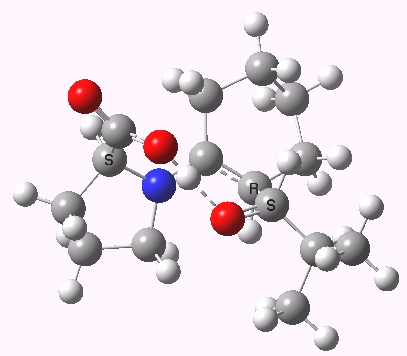
(S,R) Houk-List transition state, updated geometry. Click for 3D
- The most significant changes involve the O…H—O bond lengths. Respectively 1.13/1.31Å in the original, they change to 1.06/1.40Å at the new level.
- The forming C-C bond changes in length from 1.89 to 2.05Å (the latter, it has to be said, being a much more “normal” value for a transition state).
- Whilst these might not seem very great changes, we do not yet know how they might impact upon the relative free energies of the four transition states. Houk and List reported the (S,R), (R,R), (S,S) and (R,S) relative free energies as 0.0, 6.7, 7.8 and 4.6 kcal/mol. The updated values for (S,R), (R,R), (S,S) and (R,S) [click on preceding links to view models] are 0.0, 6.0, 5.7 and 5.4 kcal/mol [click on preceding links to view calculation archives], which represent only minor changes to these energies.
- The (S,S) diastereoisomer is an interesting outlier. The transition state normal mode wave numbers are -373, -481, -815 and -402 cm-1 respectively and the O…H…O bond lengths for (S,S) are 1.18 and 1.20Å, a rather more symmetrical proton transfer than the other three.
Which brings us to the main point; what is the origin of the diastereoselectivity? An NBO analysis can compare the total steric exchange energy (due to Pauli bond-bond repulsions) of the four isomers, which turns out to be respectively 1214, 1221, 1235 and 1229 kcal/mol. In other words, the favoured isomer has the smallest steric exchange energy. Of course this one term is not the only contributing factor, and a more elaborate analysis will no doubt provide further insight.
So an update to the Houk-List transition state reveals the general characteristics are intact and it is still a very useful model for analysing stereoselectivity in proline organocatalysis.
Postscript: The Intrinsic reaction coordinate (for (S,S) ) is shown below.
Tags: catalysis, condensation, energy, gas-phase optimised geometry, Historical, Houk-List, smallest steric exchange energy, so-called single-point solvation energy correction, steric exchange energy
Of course 9 years have passed since the original studies and there has been a huge progress in theoretical chemistry and computational power, so there is no need to stick to the old methods. But I’m nevertheless curious if the changes of the TS geometry (and therefore energies) are mainly because of optimization using solvation model or better functional and basis set?
Did you try optimizing the TS using ωB97XD/6-311G(d,p) without SCRF? If yes, how big are the differences?
I have not done all the control experiments, but my experience is that the differences are largely due to the inclusion of solvation as part of the geometry optimisation. These transition states have dipole moments of around 10D, and at this magnitude, (continuum) solvation does start affecting the computed geometries. Of course, adding explicit solvent, by forming hydrogen bonds to the ends of the dipole can also affect the geometry.
It would also be true to say that for the explicit case of proton transfers, these can be VERY sensitive to the functional, and to how correlation is treated. For such a simple reaction, it can be a complicated one to get right, as perhaps this post suggests.
[…] 2007) using a somewhat updated procedure, much in the same way that the transition state for the aldol reaction was. A ωB97XD/6-311G(d,p)/SCRF=dichloromethane calculation of step (b) gives the transition state […]
[…] Stereoselectivities of Proline-Catalyzed Asymmetric Intermolecular Aldol Reactions. […]