The Bürgi–Dunitz angle is one of those memes that most students of organic chemistry remember. It hypothesizes the geometry of attack of a nucleophile on a trigonal unsaturated (sp2) carbon in a molecule such as ketone, aldehyde, ester, and amide carbonyl. Its value obviously depends on the exact system, but is generally taken to be in the range 105-107°. A very good test of this approach is to search the crystal structure database (this was how it was originally established[1]).
 The search is defined as follows
The search is defined as follows
- R can be either H or C
- The carbon is constrained to 3-coordinate
- The carbonyl oxygen is constrained to 1-coordinate
- QA can be any of N, O, S, Cl, F.
- QB can be any of H (aldehyde), C (ketone), N (amide), O (ester) or S (thioester).
- The distance QA…C is constrained to any intermolecular non-bonded contact ≤ the sum of the van der Waals radii of the two atoms involved and the angle QA…C=O is the Bürgi–Dunitz angle.
- I have also added a torsion constraint to specify that Nu has got to be ± 20° from orthogonality to the plane of the carbonyl to allow it to attack the π* orbital.
- The crystallographic R factor must be < 0.05, no disorder, no crystallographic errors and the temperature is either any or < 120K.
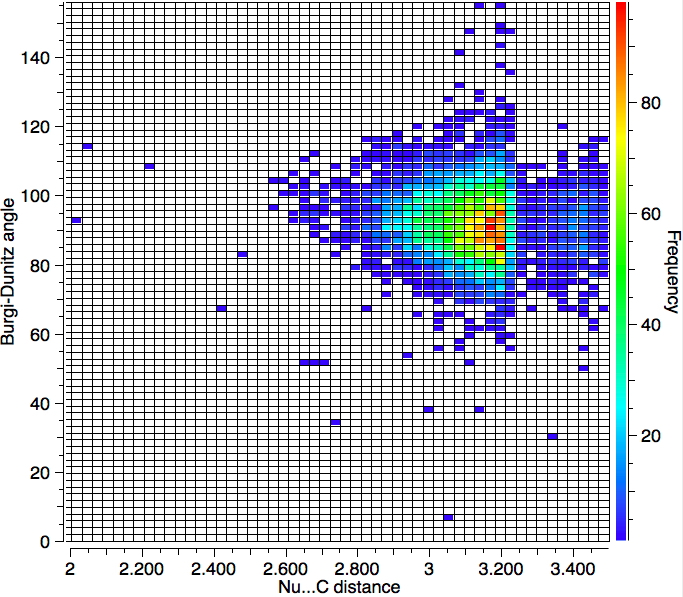
With no temperature specified, 6994 hits are obtained as below. So the most probable angle (red spot) is ~90°.
One important change to the search is to decrease the temperature to 120K, since structures will have less vibrational noise. The number of hits decreases to 1279, but the most probable angle if anything reduces slightly.
So we have something of a mystery; this crystallographic data shows an angle of approach about 15° less than the oft quoted value. Here are some thoughts:
- This search is the average for all types of carbonyl, whereas the original suggestion was constrained to four types of nucleophiles and simple ketones.
- This search extends the interacting distance of the nucleophile and the carbon out to 3.5Å which is significantly longer than the normally considered length of ~2.85Å. The hotspots occur at about 3.15Å and not 2.85Å.
- There is obviously considerably more data available in 2015 than in 1974, and in particular at low temperature.
- The Bürgi–Dunitz angle is in fact one of two defining the trajectory, the other being the Flippin–Lodge angle which defines the displacement towards R or QB. The search above gives no direct information about this angle, but the torsion is related since it is constrained to bisect the C=O to within ± 20° and hence bisect the groups R and QB.
- An angle of ≤ 90° does not match to the normal explanation, which is that the nucleophile attacks the π* orbital, each lobe of which "leans out" from the centre at about 105° rather than leaning in at ≤ 90°.
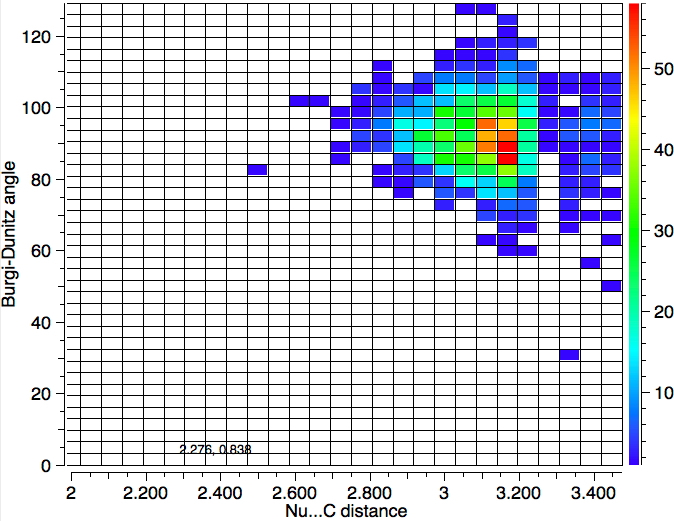
- Decreasing the torsion range to ± 5° at 120K gives 592 hits with a hot spot at 95°
- Also constraining the distance QA…C to be 0.3Å less than the van der Waals sum at 120K gives 59 hits with a hot spot at 95° and 2.9Å.
Well, to get to the bottom of this will require reducing the scope of both QA and QB, to find which if any of discrete values for these two variables can indeed give an angle of 105-107°. This would make for quite a good student group project; I expect a group of 8 students could sort this out quite quickly!
Acknowledgments
This post has been cross-posted in PDF format at Authorea.
References
- H. B:urgi, J. Dunitz, J. Lehn, and G. Wipff, "Stereochemistry of reaction paths at carbonyl centres", Tetrahedron, vol. 30, pp. 1563-1572, 1974. https://doi.org/10.1016/s0040-4020(01)90678-7
Tags: alkene, Bürgi–Dunitz angle, Carbonyl, Chemistry, Functional groups, Group of Eight, Ketone, Organic chemistry, Organic compounds, Stall
Could you tell me, what structural data base did you use during your searches?
The Cambridge Crystal Structure Database.
This is a really nice exercise for students (or any reader in general) to revisit the published data and theory critically!
I believe that the primary source of the discrepancy comes from the overwhelming number of structures featuring antiparallel C=O interactions. In those cases, the O of one moiety sits on the C of the other, resulting in O…C=O angle at ~90 degrees.
Restricting the nucleophile to tertiary amines will significantly clean up the search results (but reducing the number of hits). Also, CSD Conquest searches by default only consider intermolecular contacts; this setting can be changed to include the intramolecular cases. This search is closer to the original Bürgi–Dunitz papers (JACS 1973, 95, 5056 and Tetrahedron 1974, 30, 1563, where 6 structures were examined!). A Conquest query file and the hitlist of such a search can be downloaded here: https://bit.ly/2SVxjWX ; the mean value of this angle is about 104 degrees.
The possibility of hydrogen bonding in the case of primary and secondary amines and the various O nucleophiles will undoubtedly complicate the analysis. The latter has been partially examined in Bürgi–Dunitz’s paper in Acta Cryst. 1974, B30, 1517.