Posts Tagged ‘pence’
Sunday, April 26th, 2015
Allotropes are differing structural forms of the elements. The best known example is that of carbon, which comes as diamond and graphite, along with the relatively recently discovered fullerenes and now graphenes. Here I ponder whether any of the halogens can have allotropes.
(more…)
Tags:Allotropy, Bromine, Carbon, Chemical elements, Chemistry, free energy barrier, Fullerene, Halogen, Hypobromite, Matter, Nonmetals, Oxidizing agents, Oxygen, pence
Posted in reaction mechanism | 9 Comments »
Friday, April 10th, 2015
Previously on this blog: modelling the reduction of cinnamaldehyde using one molecule of lithal shows easy reduction of the carbonyl but a high barrier at the next stage, the reduction of the double bond. Here is a quantum energetic exploration of what might happen when a second LAH is added to the brew (the usual ωB97XD/6-311+G(d,p)/SCRF=diethyl ether).
(more…)
Tags:computed free energy barrier, energy, energy surface, final product, flat energy potential, free energy, lower energy pathways, metal exchange, pence, potential energy surface, reduction, Yes
Posted in reaction mechanism | No Comments »
Wednesday, April 1st, 2015
The reduction of cinnamaldehyde by lithium aluminium hydride (LAH) was reported in a classic series of experiments[1],[2],[3] dating from 1947-8. The reaction was first introduced into the organic chemistry laboratories here at Imperial College decades ago, vanished for a short period, and has recently been reintroduced again.‡ The experiment is really simple in concept; add LAH to cinnamaldehyde and you get just reduction of the carbonyl group; invert the order of addition and you additionally get reduction of the double bond. Here I investigate the mechanism of these reductions using computation (ωB97XD/6-311+G(d,p)/SCRF=diethyl ether).
(more…)
References
- R.F. Nystrom, and W.G. Brown, "Reduction of Organic Compounds by Lithium Aluminum Hydride. I. Aldehydes, Ketones, Esters, Acid Chlorides and Acid Anhydrides", Journal of the American Chemical Society, vol. 69, pp. 1197-1199, 1947. https://doi.org/10.1021/ja01197a060
- R.F. Nystrom, and W.G. Brown, "Reduction of Organic Compounds by Lithium Aluminum Hydride. II. Carboxylic Acids", Journal of the American Chemical Society, vol. 69, pp. 2548-2549, 1947. https://doi.org/10.1021/ja01202a082
- F.A. Hochstein, and W.G. Brown, "Addition of Lithium Aluminum Hydride to Double Bonds", Journal of the American Chemical Society, vol. 70, pp. 3484-3486, 1948. https://doi.org/10.1021/ja01190a082
Tags:Al-H-Li bridge, dihydrocinnamyl alcohol reduction product, free energy, Imperial College, independent researcher, low energy escape route, lower energy alternative, metal, pence
Posted in reaction mechanism | 5 Comments »
Sunday, March 15th, 2015
My previous posts have covered the ionization by a small number of discrete water molecules of the series of halogen acids, ranging from HI (the strongest, pKa -10) via HF (weaker, pKa 3.1) to the pseudo-halogen HCN (the weakest, pKa 9.2). Here I try out some even stronger acids to see what the least number of water molecule needed to ionize these might be.
(more…)
Tags:Christopher Reed, Ohio, pence
Posted in Interesting chemistry | 3 Comments »
Saturday, February 14th, 2015
According to Guggemos, Slavicek and Kresin, about 5-6![1]. This is one of those simple ideas, which is probably quite tough to do experimentally. It involved blasting water vapour through a pinhole, adding HCl and measuring the dipole-moment induced deflection by an electric field. They found “evidence for a noticeable rise in the dipole moment occurring at n≈5–6“.
(more…)
References
- N. Guggemos, P. Slavíček, and V.V. Kresin, "Electric Dipole Moments of Nanosolvated Acid Molecules in Water Clusters", Physical Review Letters, vol. 114, 2015. https://doi.org/10.1103/physrevlett.114.043401
Tags:energy, gas phase models, Java, pence, similar energy
Posted in Interesting chemistry, reaction mechanism | 1 Comment »
Monday, December 22nd, 2014
I started chemistry with a boxed set in 1962. In those days they contained serious amounts of chemicals, but I very soon ran out of most of them. Two discoveries turned what might have been a typical discarded christmas present into a lifelong career and hobby.
(more…)
Tags:A. N. Beck and Sons, Albert N. Beck, chemical stains, chemicals, chemist, christmas, Craven Cottage, GBP, London, pence, Shilling
Posted in Historical | 57 Comments »
Saturday, July 19th, 2014
Whilst clusters of carbon atoms are well-known, my eye was caught by a recent article describing the detection of a cluster of boron atoms, B40 to be specific.[1] My interest was in how the σ and π-electrons were partitioned. In a C40, one can reliably predict that each carbon would contribute precisely one π-electron. But boron, being more electropositive, does not always play like that. Having one electron less per atom, one might imagine that a fullerene-like boron cluster would have no π-electrons. But the element has a propensity[2] to promote its σ-electrons into the π-manifold, leaving a σ-hole. So how many π-electrons does B40 have? These sorts of clusters are difficult to build using regular structure editors, and so coordinates are essential. The starting point for a set of coordinates with which to compute a wavefunction was the supporting information. Here is the relevant page: 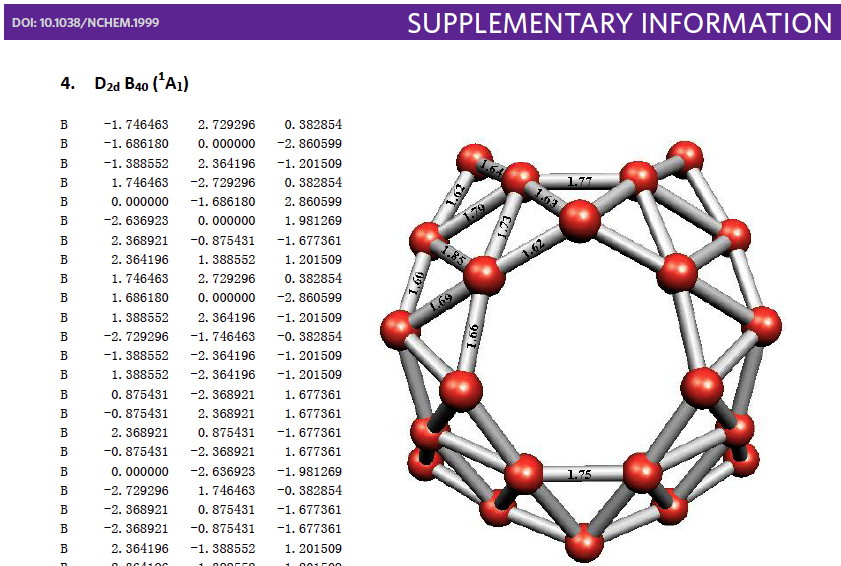 The coordinates are certainly there (that is not always the case), but you have to know a few tricks to make them usable.
The coordinates are certainly there (that is not always the case), but you have to know a few tricks to make them usable.
(more…)
References
- H. Zhai, Y. Zhao, W. Li, Q. Chen, H. Bai, H. Hu, Z.A. Piazza, W. Tian, H. Lu, Y. Wu, Y. Mu, G. Wei, Z. Liu, J. Li, S. Li, and L. Wang, "Observation of an all-boron fullerene", Nature Chemistry, vol. 6, pp. 727-731, 2014. https://doi.org/10.1038/nchem.1999
- H.S. Rzepa, "The distortivity of π-electrons in conjugated boron rings", Physical Chemistry Chemical Physics, vol. 11, pp. 10042, 2009. https://doi.org/10.1039/b911817a
Tags:Acrobat, Adobe, chemical markup, DOS, operating systems, PDF, pence, Unix
Posted in Chemical IT, Interesting chemistry | 2 Comments »
Saturday, July 12th, 2014
Computational quantum chemistry has made fantastic strides in the last 30 years. Often deep insight into all sorts of questions regarding reactions and structures of molecules has become possible. But sometimes the simplest of questions can prove incredibly difficult to answer. One such is how accurately can the boiling point of water be predicted from first principles? Or its melting point? Another classic case is why mercury is a liquid at room temperatures? The answer to that question (along with another, why is gold the colour it is?) is often anecdotally attributed to Einstein. More accurately, to his special theory of relativity.[1] But finally in 2013 a computational proof of this was demonstrated for mercury.[2] The proof was built up in three stages.
(more…)
References
- A. Einstein, "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?", Annalen der Physik, vol. 323, pp. 639-641, 1905. https://doi.org/10.1002/andp.19053231314
- F. Calvo, E. Pahl, M. Wormit, and P. Schwerdtfeger, "Evidence for Low‐Temperature Melting of Mercury owing to Relativity", Angewandte Chemie International Edition, vol. 52, pp. 7583-7585, 2013. https://doi.org/10.1002/anie.201302742
Tags:bulk metal, pence, potential energy surfaces
Posted in General | 4 Comments »
