Five years back, I speculated about the mechanism of the epoxidation of ethene by a peracid, concluding that kinetic isotope effects provided interesting evidence that this mechanism is highly asynchronous and involves a so-called “hidden intermediate”. Here I revisit this reaction in which a small change is applied to the atoms involved.
Posts Tagged ‘Kinetic isotope effect’
Epoxidation of ethene: a new substituent twist.
Friday, December 21st, 2018I’ve started so I’ll finish. The mechanism of diazo coupling to indoles – forty (three) years on!
Thursday, December 24th, 2015
The BBC TV quiz series Mastermind was first broadcast in the UK in 1972, the same time I was starting to investigate the mechanism of diazocoupling to substituted indoles as part of my Ph.D. researches. The BBC program became known for the catch phrase I've started so I'll finish; here I will try to follow this precept with the project I started then. In 1972, one measured the rates of chemical reactions to gain insights into the transition state kinetic model. To obtain more data, we used isotopes such as 2H or 3H, together with substituents such as R-t-butyl to modify the potential energy surfaces of the reactions by inducing steric effects.[1],[2] We found that the kinetics for this reaction were actually complex‡ (in part because of pH dependence) involving a Wheland intermediate (the formation of which is shown with red curly arrows above) followed by the collapse of this intermediate to the diazo-coupled product (blue arrows). Coupling to 2-methyl indole (R=X=H, R'=Me), 2-t-butyl indole (R=H, R'=t-butyl) and 4-methyl-2-t-butyl indole (R=Me, R'=t-butyl) revealed that the kinetic isotope effects induced by replacing H by D or T were "not apparent" (i.e. close to 1), the inference being that the rate constant k1 for those systems was slower than k2; the formation of the Wheland intermediate was rate determining (the rds) for the reaction. But with 2-methyl-4,6-di-t-butyl indole (R=t-butyl, R'=Me) this changed and a deuterium isotope effect of ~7 was observed. The rate determining proton removal from the Wheland intermediate k2 was now slower than k1. With 2,4,6-tri-t-butyl indole, we ended by noting that the reaction become almost too slow to observe and furthermore was accompanied by loss of a t-butyl cation as well as a proton. At this point we attempted to infer some transition state models consistent with these observations. Note that we had relatively little data with which to derive our 3D models (one needs to define a geometry using 3N-6 variables, along with its relative energy and force constants). The text and diagram of our attempt is shown below.
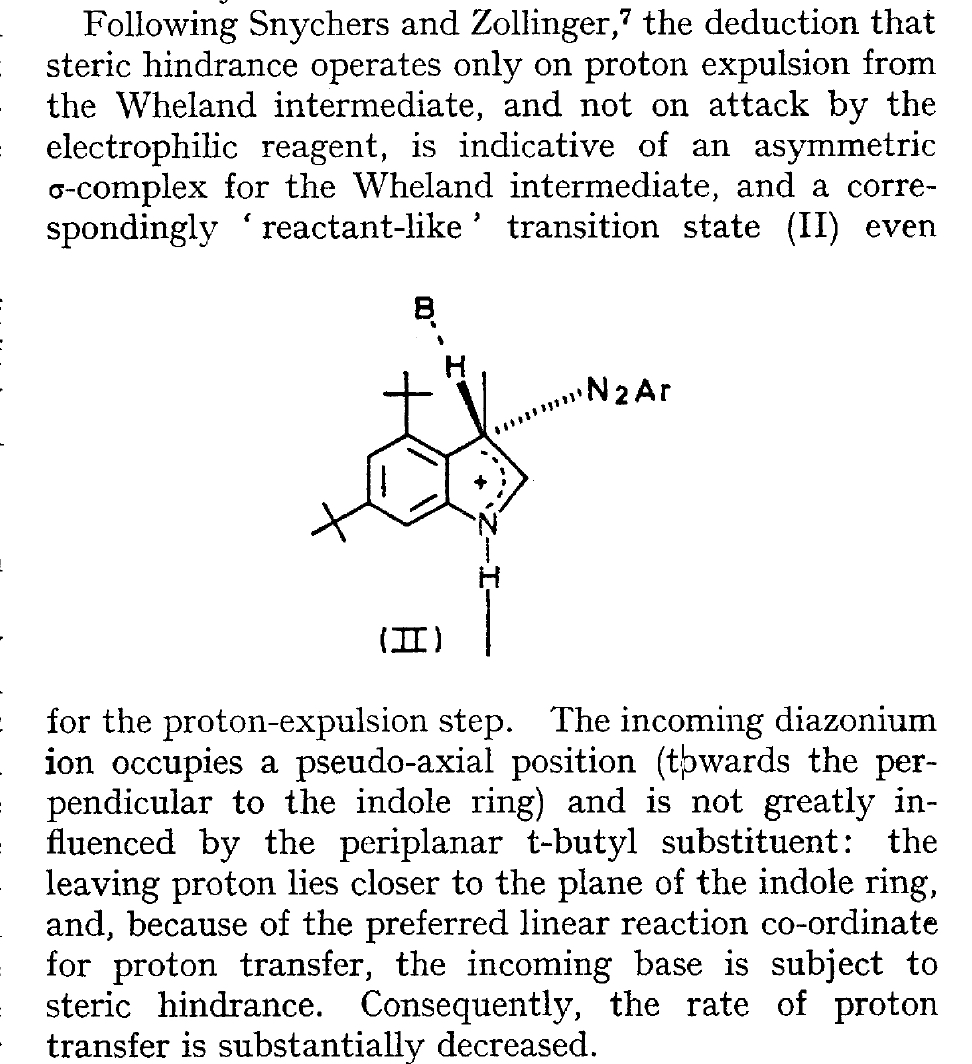 The main points of this argument were;
The main points of this argument were;
References
- B.C. Challis, and H.S. Rzepa, "The mechanism of diazo-coupling to indoles and the effect of steric hindrance on the rate-limiting step", Journal of the Chemical Society, Perkin Transactions 2, pp. 1209, 1975. https://doi.org/10.1039/p29750001209
- H.S. Rzepa, "Hydrogen Transfer Reactions Of Indoles", Zenodo, 1974. https://doi.org/10.5281/zenodo.18777
Reproducibility in science: calculated kinetic isotope effects for cyclopropyl carbinyl radical.
Saturday, July 11th, 2015Previously on the kinetic isotope effects for the Baeyer-Villiger reaction, I was discussing whether a realistic computed model could be constructed for the mechanism. The measured KIE or kinetic isotope effects (along with the approximate rate of the reaction) were to be our reality check. I had used ΔΔG energy differences and then HRR (harmonic rate ratios) to compute[1] the KIE, and Dan Singleton asked if I had included heavy atom tunnelling corrections in the calculation, which I had not. His group has shown these are not negligible for low-barrier reactions such as ring opening of cyclopropyl carbinyl radical.[2] As a prelude to configuring his suggested programs for computing tunnelling (GAUSSRATE and POLYRATE), it was important I learnt how to reproduce his KIE values.[2] Hence the title of this post. Now, read on.
References
- H.S. Rzepa, "KINISOT. A basic program to calculate kinetic isotope effects using normal coordinate analysis of transition state and reactants.", 2015. https://doi.org/10.5281/zenodo.19272
- O.M. Gonzalez-James, X. Zhang, A. Datta, D.A. Hrovat, W.T. Borden, and D.A. Singleton, "Experimental Evidence for Heavy-Atom Tunneling in the Ring-Opening of Cyclopropylcarbinyl Radical from Intramolecular <sup>12</sup>C/<sup>13</sup>C Kinetic Isotope Effects", Journal of the American Chemical Society, vol. 132, pp. 12548-12549, 2010. https://doi.org/10.1021/ja1055593
Reproducibility in science: calculated kinetic isotope effects for the Baeyer-Villiger reaction.
Wednesday, July 1st, 2015Recollect this earlier post on the topic of the Baeyer-Villiger reaction. In 1999 natural abundance kinetic isotope effects were reported[1] and I set out to calculate the values predicted for a particular model constructed using Quantum mechanics. This comparison of measurement and calculation is nowadays a standard verification of both experiment and theory. When the two disagree either the computational model is wrong or incomplete, or the remoter possibility that there is something not understood about the experiment.
References
- D.A. Singleton, and M.J. Szymanski, "Simultaneous Determination of Intermolecular and Intramolecular <sup>13</sup>C and <sup>2</sup>H Kinetic Isotope Effects at Natural Abundance", Journal of the American Chemical Society, vol. 121, pp. 9455-9456, 1999. https://doi.org/10.1021/ja992016z
Natural abundance kinetic isotope effects: mechanism of the Baeyer-Villiger reaction.
Wednesday, June 10th, 2015I have blogged before about the mechanism of this classical oxidation reaction. Here I further explore computed models, and whether they match the observed kinetic isotope effects (KIE) obtained using the natural-abundance method described in the previous post.
Natural abundance kinetic isotope effects: expt. vs theory.
Wednesday, June 3rd, 2015My PhD thesis involved determining kinetic isotope effects (KIE) for aromatic electrophilic substitution reactions in an effort to learn more about the nature of the transition states involved.[1] I learnt relatively little, mostly because a transition state geometry is defined by 3N-6 variables (N = number of atoms) and its force constants by even more and you get only one or two measured KIE per reaction; a rather under-defined problem in terms of data! So I decided to spend a PostDoc learning how to invert the problem by computing the anticipated isotope effects using quantum mechanics and then comparing the predictions with measured KIE.[2] Although such computation allows access to ALL possible isotope effects, the problem is still under-defined because of the lack of measured KIE to compare the predictions with. In 1995 Dan Singleton and Allen Thomas reported an elegant strategy to this very problem by proposing a remarkably simple method for obtaining KIE using natural isotopic abundances.[3] It allows isotope effects to be measured for all the positions in one of the reactant molecules by running the reaction close to completion and then recovering unreacted reactant and measuring the changes in its isotope abundances using NMR. The method has since been widely applied[4],[5] and improved.[6] Here I explore how measured and calculated KIE can be reconciled.
References
- B.C. Challis, and H.S. Rzepa, "The mechanism of diazo-coupling to indoles and the effect of steric hindrance on the rate-limiting step", Journal of the Chemical Society, Perkin Transactions 2, pp. 1209, 1975. https://doi.org/10.1039/p29750001209
- M.J.S. Dewar, S. Olivella, and H.S. Rzepa, "Ground states of molecules. 49. MINDO/3 study of the retro-Diels-Alder reaction of cyclohexene", Journal of the American Chemical Society, vol. 100, pp. 5650-5659, 1978. https://doi.org/10.1021/ja00486a013
- D.A. Singleton, and A.A. Thomas, "High-Precision Simultaneous Determination of Multiple Small Kinetic Isotope Effects at Natural Abundance", Journal of the American Chemical Society, vol. 117, pp. 9357-9358, 1995. https://doi.org/10.1021/ja00141a030
- Y. Wu, R.P. Singh, and L. Deng, "Asymmetric Olefin Isomerization of Butenolides via Proton Transfer Catalysis by an Organic Molecule", Journal of the American Chemical Society, vol. 133, pp. 12458-12461, 2011. https://doi.org/10.1021/ja205674x
- J. Chan, A.R. Lewis, M. Gilbert, M. Karwaski, and A.J. Bennet, "A direct NMR method for the measurement of competitive kinetic isotope effects", Nature Chemical Biology, vol. 6, pp. 405-407, 2010. https://doi.org/10.1038/nchembio.352