I conclude my exploration of conformational preferences by taking a look at esters. As before, I start with a search definition, the ester being restricted to one bearing only sp3 carbon centers.
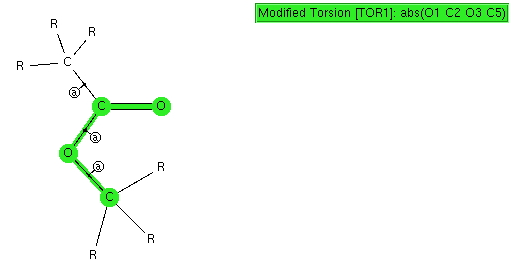
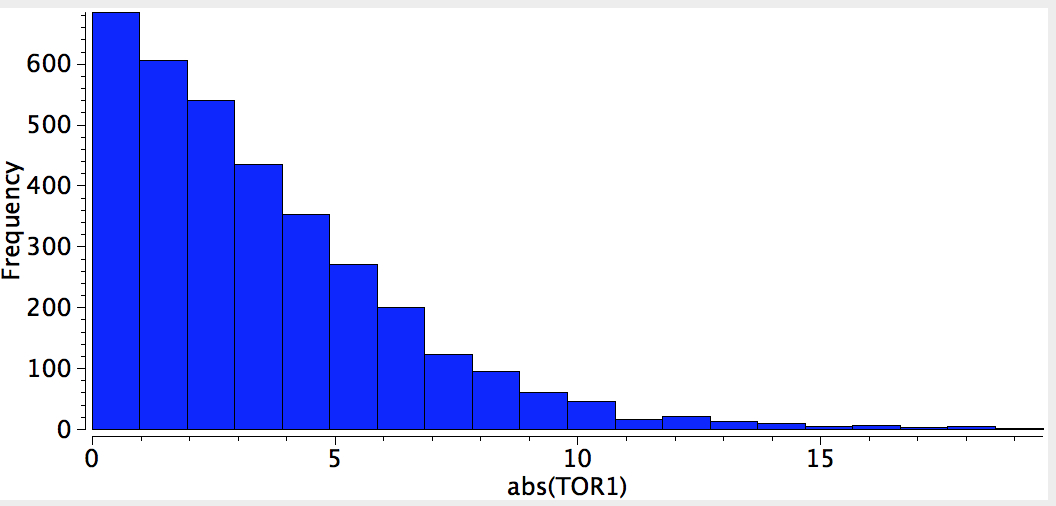
The result of such a search is pretty clear-cut; they all exist in just one conformation, the s-cis, in which a lone pair of electrons on the alkyl-oxygen is aligned quite precisely anti-periplanar with the axis of the C=O bond. This very narrow distribution suggests a relatively large energy preference for this orientation, and we need to seek its origins.
This arises from two electronic alignments. The first orients the in-plane alkyl oxygen lone pair (orange-purple below) anti-periplanar with the C=O σ* empty orbital (red-blue; orange=red, blue=purple), an interaction mapping to 7.7 kcal/mol in the NBO E(2) energy. The second reinforcement (not shown) aligns the (O=)C-Me donor bond with the antiperiplanar O-Me acceptor (5.3 kcal/mol). These two interactions are weaker in the s-trans ester, which is 8.1 kcal/mol higher in ΔG298 and for which the E(2) terms are respectively 3.0 and 0.6 kcal/mol.
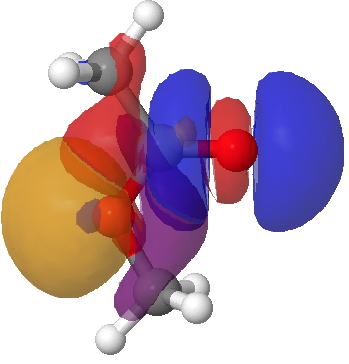
Lp(alkyl-O)/C=O σ* Click for 3D.
But wait, this interaction has electrons moving from the alkyl oxygen to the acyl oxygen (red arrows below) and apparently weakening the C=O bond in the process. But in an entirely different context, we learn that the C=O vibrational stretching wavenumber for an ester (1750 cm-1) is higher than that of a ketone (~1715 cm-1); the C=O is stronger rather than weaker in the ester. So now we have to move the σ-electrons back again (green arrows below).
This strengthening of the C=O bond arises from the following overlap of the σ-lone pair on the carbonyl oxygen with the alkyl-O-C σ* empty orbital, for which E(2) is 41.5 kcal/mol, much larger than the previous effect. It however does NOT discriminate between the s-cis and s-trans conformations, since this interaction is almost the same in the latter (41.8). So we have a to-of-(red)-electrons which promote the s-cis conformation, and rather stronger fro-of-(green)-electrons which strengthen the C=O bond. But they do not cancel each-other; each has its own job to do!
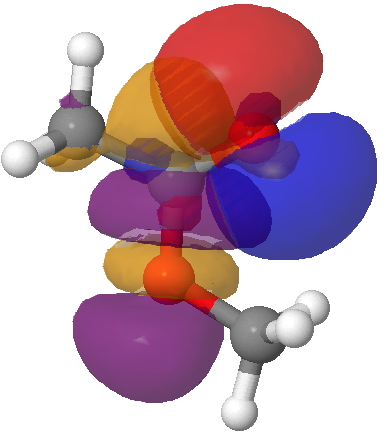
Lp(acyl-O)/C-O σ* Click for 3D.
There is one other overlap which may differentiate between s-cis and s-trans, but a rather less obvious one. That is the alkyl-Oπ donating to the acyl C=Oπ* which has E(2) 64.7 for the former and 59.4 kcal/mol for the latter. It is not immediately apparent why this overlap should favour s-cis. It is however the effect that induces a significant rotational barrier about the C-O bond (~12 kcal/mol).
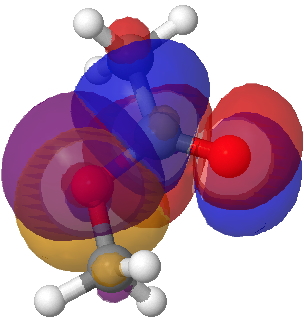
Lp (alkyl-O π)/C=O π* Click for 3D.
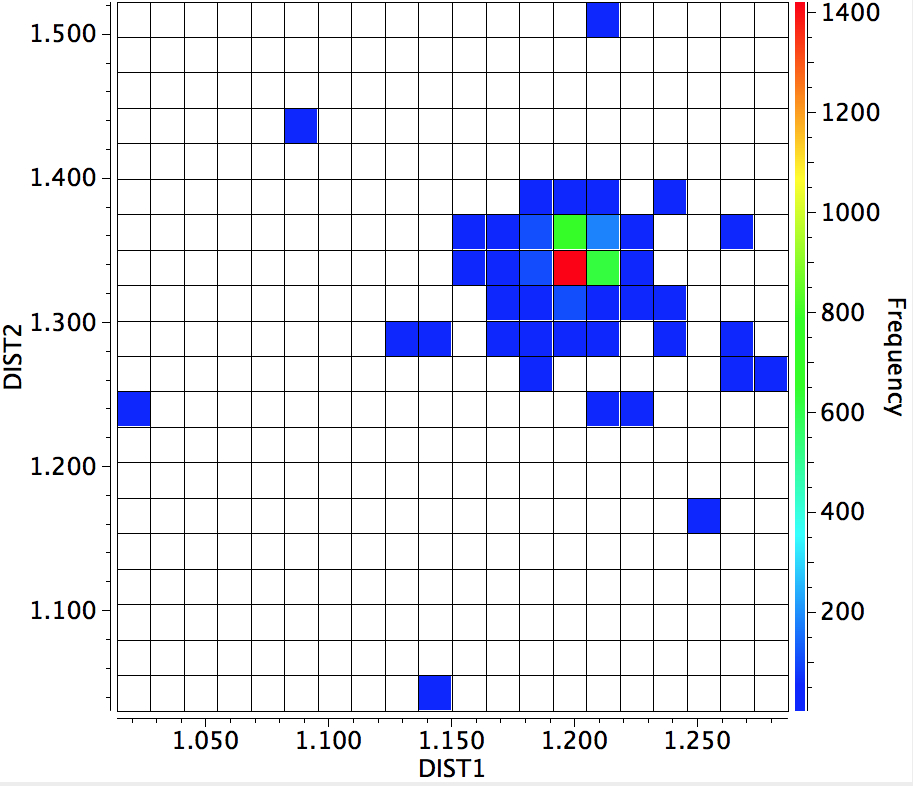
Here is the result of another search of the crystal database; namely the C=O distance (DIST1) vs the C-O distance (DIST2). You can see that the red hot spot (~1400 examples) is very isolated (the blue squares represent < 200 hits), and there seems to be no significant correlation between the two lengths and the structure.
I will conclude with a brief discussion of the carbonyl lone pairs. There are two, and one of them has been shown above in the Lp(acyl-O)/C-O σ* interaction. There is another, but it plays no role in the conformation, and is of quite a different character. Although a low-lying orbital, it is clearly non bonding; indeed might be slightly anti-bonding along the C=O axis. These two carbonyl lone pairs are quite different in character, since each performs a different role in the molecule.
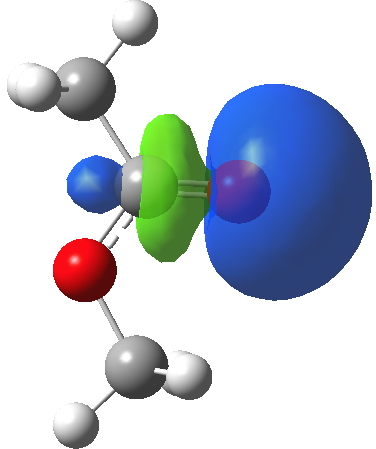
Click for 3D.
So the conformational analysis of this simple little molecule reveals some interesting toos-and-fros in the electrons. I will deal with the issue of the carbonyl stretching frequencies in another post.
Tags: conformational analysis, energy, large energy preference, search definition, Tutorial material