My last comment as appended to the previous post promised to analyse two so-called extended porphyrins for their topological descriptors. I start with the Cãlugãreanu/Fuller theorem which decomposes the topology of a space curve into two components, its twist (Tw) and its writhe (Wr, this latter being the extent to which coiling of the central curve has relieved local twisting) and establishes a topological invariant called the linking number[cite]10.1021/ja710438j[/cite]
Lk = Tw + Wr
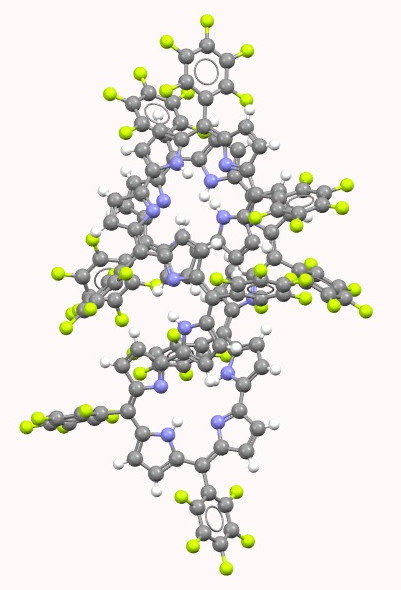 HIYTAL. Click for 3D. |
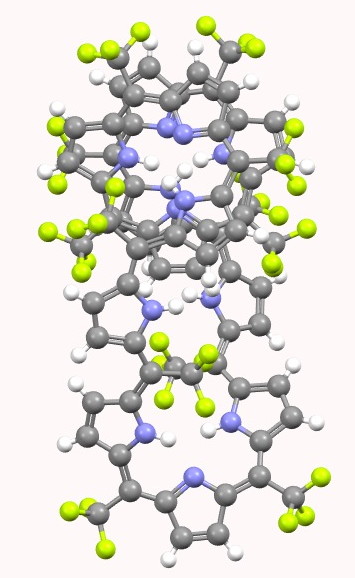 SELQUW. Click for 3D. |
Visual inspection of the models above (I really do encourage you to click on the images to load the 3D coordinates) reveals that HIYTAL[cite]10.1002/chem.200701909[/cite] has a major coil that forms one and a half helical turns in a clockwise direction, and a loop connecting the ends of the coil which forms a half-helical turn in an anti-clockwise direction. SELQUW[cite]10.1002/chem.200600158[/cite] has a major coil comprising one and half helical turns in an anti-clockwise direction and a connecting loop which also coils anti-clockwise. So the former sustains a total of one full (clockwise) helical turn and the latter two full (anti-clockwise) helical turns.
The nomenclature for helical molecules includes a chiral descriptor P (for a positive helical turn) and M (for a negative helical turn). What such a descriptor does not do is quantify the total number of helices describing the topology. So I suggest we use instead the linking number Lk. Instead of P and M, we have positive and negative integers (in units of 2π) providing this quantitative information.
The linking number analysis for these two molecules comes out as below.‡ I have multiplied the linking number unit from 2π to 1π for a reason that I will explain shortly:
| π-electrons | Lk | Tw | Wr | Δr (meso) | |
| SELQUW | 56=4n | -4 | -1.34 | -2.66 | 0.048 |
| HIYTAL | 62=4n+2 | +2 | +0.46 | +1.54 | 0.045 |
You can see that the linking numbers (and their signs) correspond exactly to the visual analysis of the helical turns above. My reason for including the factor of 2 is that it enables us to make a further link to the Hückel aromaticity rule:
- Cyclic conjugated systems are aromatic if they contain 4n+2 π-electrons and have an even or zero linking number (in units of 1π).
- Cyclic conjugated systems are aromatic if they contain 4n π-electrons and have an odd linking number (in units of 1π).
- Cyclic conjugated systems are anti-aromatic if they contain 4n π-electrons and have an even or zero linking number (in units of 1π).
- Cyclic conjugated systems are anti-aromatic if they contain 4n+2 π-electrons and have an odd linking number (in units of 1π).
By these rules, SELQUW contains (by the shortest path) 56 π-electrons, belongs to the 4n electron rule (n=14) and hence is formally anti-aromatic (rule 3 above). HIYTAL has a path of 62-electrons, belongs to the 4n+2 rule (n=15) and hence is formally aromatic (rule 1 above).
For systems with so many (correlated) electrons, it is probably tenuous to make a connection between the bond-length alternation at the meso position and the aromaticity (or lack of it). I comment only that HIYTAL converts more of the coiling into writhing of the central curve than does SELQUW, and this destroys less π-π overlap by reducing the overall degree of twisting. I might also speculate that nevertheless a modest degree of twisting may impact upon the intrinsic distortivity of π-electrons in cyclically conjugated systems (such as that in benzene[cite]10.1021/cr990363l[/cite]), as noted in this earlier post. Such effects may make the interpretation of bond-alternation in such helical systems more difficult.
‡ A program for calculating these components can be found here. For a fun-packed journey through linking numbers and the association with valentine cards, go see this post here!