Although have dealt with the π-complex formed by protonation of PhNHOPh in several posts, there was one aspect that I had not really answered; what is the most appropriate description of its electronic nature? Here I do not so much provide an answer, as try to show how difficult getting an accurate answer might be.
In an earlier post, I had shown how an in-phase combination of the HOMO of the anion 1 with the LUMO of the cation 2 led to an occupied molecular orbital for the complex (below, left). An out-of-phase combination of these two gives instead the LUMO of the π-complex (below, right). It might seem as if a pair of electrons would like to occupy the first of these, and indeed a wavefunction constructed on this basis (using this occupancy as the single reference; indeed only state) resulted in the conclusion that the complex was aromatic. The diatropicity (~magnetic aromaticity) was strongest in the region between the two stacked rings, and the individual rings themselves had lost their local aromaticity. One might then infer that a wavefunction constructed by populating the LUMO below would in fact rearrange the aromaticity, returning this property back to the two individual rings. There would in fact be apparently nothing to keep the rings stacked, and so in the limit this wavefunction would correspond to a biradical (both states would be degenerate and hence have one electron in each).
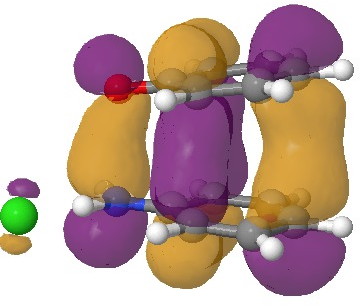 The π-complex HOMO. Click for 3D. |
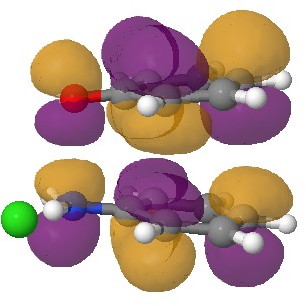 The π-complex LUMO. Click for 3D |
So where along this spectrum of possible interpretations does a more realistic wavefunction settle? To answer this question, we must optimise the self-consistent field describing the electronic structure using BOTH electronic configurations (as a first approximation). This method is known as a multi-reference configuration interaction or CASSCF (complete active space self-consistent field) approach. Technically, the variation principle of minimising the electronic energy is applied to all the eigenvalues of the CI matrix, and not just the single reference state as is normally done. The simplest approach to the molecule above is to consider the active space as just the two orbitals above (the inactive space is represented by all the remaining doubly occupied and unoccupied orbitals), resulting in a CI determinant with three solutions (two electrons in the HOMO, two electrons on the LUMO and one electron in each). One would then use the energy computed from this multi-reference solution to re-optimise the geometry of the π-complex. This would then surely be a “better” description of the wavefunction for this molecule. Or would it? Well, this is what happened when I tried.
- I took the geometry previously found for the π-complex (it is pertinent that this was obtained using a density functional method with inclusion of dispersion attractions; ωB97XD/6-311(d,p)/SCRF=water) and ran a CASSCF(2,2) calculation at that geometry (and retaining the solvent field). This means an active space of two orbitals (the two shown above) populated with two electrons in three different configurations. The answer came out that the lowest energy solution (eigenvalue) of the CI matrix had eigenvectors corresponding to 0.94 (two electrons in the HOMO) and -0.34 (two electrons in the LUMO). This translates to an electronic population of 1.77 electrons in the former and 0.23 electrons in the latter. So this molecule shows some noticeable multi-reference character. In that it resembles for example, ozone. Such molecules are often described as awkward, since the simple molecular orbital picture which we use when thinking about doubly occupied orbitals is clearly only an approximation (in this case 1.77 rather than 2.0). We often sweep this thought under the carpet.
- I then tried to optimise the geometry of the complex using this new, improved electronic description. Well, slowly, the two rings drifted apart. Very slowly! Remember we have a complex hybrid method operating here; CASSCF(2,2)/6-311G(d,p) under the influence of a continuum solvent field for water (which appears necessary to attempt to describe the nature of two ion-pairs stacking on top of each other). The CI vectors crept towards 0.75 (HOMO) and -0.67 (LUMO), corresponding to electron occupancies of 1.11 and 0.89 (almost equal, i.e. a biradical) and close to the other extreme noted above. During this process, the energy dropped by about 10 kcal/mol. So is this a more realistic solution?
- Well, we have to return to the difference between a density functional method with dispersion correction and CASSCF. The former attempts to allow for dynamic electron correlation, and this is particularly important for stacked π-rings. Getting the correct ring separation distance can only be achieved when such electron correlation is included; it is notably not obtained if a simple Hartree-Fock approach is used. CASSCF is a Hartree-Fock based method that captures the static electron correlation, but NOT that dynamic one.
- So this leads us to the next refinement, including CASSCF for static correlation and e.g. a method such as MP2 (CASPT2) to recover some dynamic correlation (and the dispersion attractions). This is tough for a molecule with 75 degrees of (geometrical) freedom, since one really needs analytical first derivatives of the energy to optimise the geometry. This combination (CASSCF, MP2, SCRF=water, analytical first derivatives) is not often found! And one I have not yet attempted to use.
What I did learn is that the balance between a mostly single-reference description of the wavefunction (occupancy of 2.0 in the HOMO above) and a multi-reference description (occupancy of 1.0 in the HOMO, 1.0 in the LUMO) is a fine one, and that balance can be perturbed by other effects, such as how one describes the correlation promoting π-stacking of the rings. And to be fair, I have not yet even found out if a CASSCF(2,2) is good enough. Perhaps it should be CASSCF(10,10), since we do have (at least) ten electrons that could populate our active space?
Of course, there are many solutions to the above problem (and some might even solve the analytical first derivatives limitation noted above). So if any reader of this blog has knowledge/expertise of this type of calculation, it would be wonderful to know what the answer is for protonated PhNHOPh. It is such an innocent molecule, and yet it seems such a challenge to properly compute its geometry (and aromaticity).