The Sharpless epoxidation of an allylic alcohol had a big impact on synthetic chemistry when it was introduced in the 1980s, and led the way for the discovery (design?) of many new asymmetric catalytic systems. Each achieves its chiral magic by control of the geometry at the transition state for the reaction, and the stabilizations (or destabilizations) that occur at that geometry. These in turn can originate from factors such as stereoelectronic control or simply by the overall sum of many small attractions and repulsions we call dispersion interactions. Here I take an initial look at these for the binuclear transition state shown schematically below.
The NCI method was described recently[cite]10.1021/ja100936w[/cite] as a method for probing the non-covalent electron density in a molecule. It does this by cleverly filtering out the covalent density via computing a first derivative of the density ρ(r) called the reduced density gradient and taking the band of values appropriate for non-covalent densities. By inspecting the Laplacian of these densities at any point in space, the region can be characterised as attractive, repulsive or neutral. Visually, this information can be transformed into isosurfaces which are colour coded depending on whether the region is attractive (=blue to green) or repulsive (yellow to red). In the previous post, it turned out that the attractive contributions to the dispersion energies differed for the two diasteromeric transition states (in the conformations calculated) by about 2.6 kcal/mol. Shown below are the two NCI surfaces for these which allow one to get some insight into where this overall contribution might come from (together with weak hydrogen bonds and other non-covalent contributions).
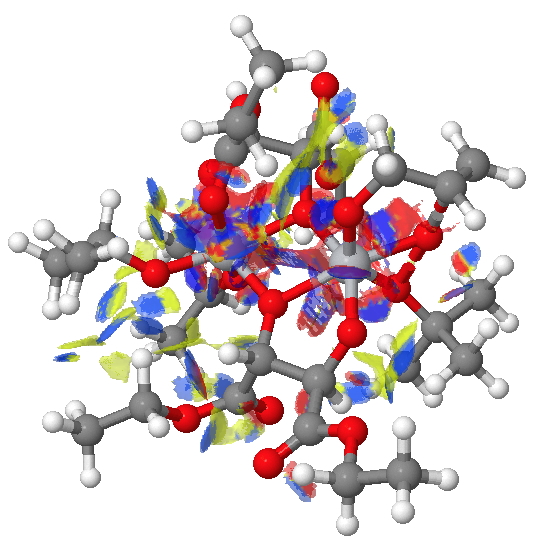 (R)-diastereomer. Click for NCI surfaces |
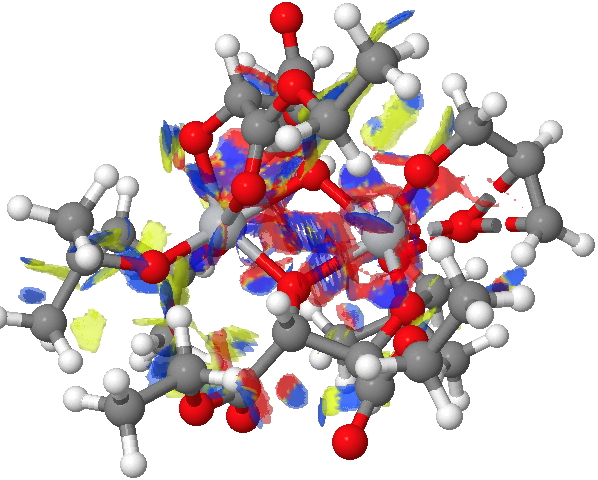 (S)-diastereomer. Click for NCI surfaces. |
Yes, it is a very complex diagram, and you really do need to study it by obtaining the 3D model and rotating it around to explore the 3D space. I would note that it is possible to integrate the NCI function (see [cite]10.1002/chem.201200547[/cite] for an example and leading references) and hence try to obtain further insights. I highlight just one here; the terminal =CH2 of the allyl alcohol points into empty space for (R), but folds back to interact with the catalyst for (S).
Finally, in case you are asking how do I obtain an NCI surface, I have created a little web site where you can submit a computed (or indeed experimental) electron density cube for processing using Jmol. Give it a go and see how it works (and thanks to Julia Contreras-Garcia and Bob Hanson for putting this together).
Tags: asymmetric catalytic systems, Bob Hanson, catalysis, Julia Contreras-Garcia, little web site, NCI, non-covalent-analysis, Reaction Mechanism, terminal =CH