Part one on this topic showed how a quantum mechanical model employing just one titanium centre was not successful in predicting the stereochemical outcome of the Sharpless asymmetric epoxidation. Here in part 2, I investigate whether a binuclear model might have more success. The new model is constructed using two units of Ti(OiPr)4, which are likely to assemble into a dimer such as that shown below (in this crystal structure, some of the iPr groups are perfluorinated).
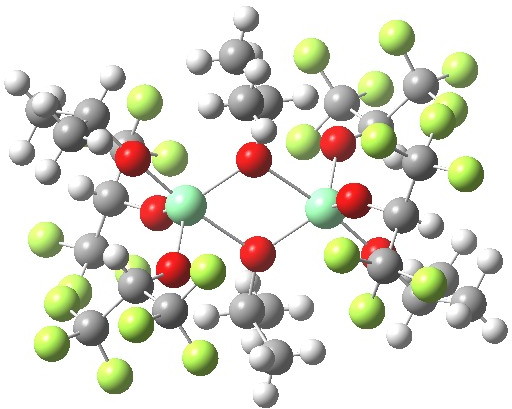
WAWBUR. Click for 3D
This allows one to construct a transition state model as follows.
- Two iPrOH molecules are displaced by diethyl tartrate for each half of the Ti2(OiPr)8, with the two metals then becoming bridged by one oxygen from each tartrate.
- Two further iPrOH are then displaced from the second Ti by one of the substrate (allyl alcohol) and one of the oxidant (t-butyl peroxide).
- The oxygen transfer now proceeds via the second (hexacoordinate) Ti. The first Ti also achieves hexa-coordination via the carbonyl oxygen of one of the tartrate ester groups. It is the geometric properties of such a hexa-coordinated Ti that in part accounts for the subtle properties of this system. Put more simply, the extra crowding at the catalytic centre of the binuclear complex restricts the space available for the transition state, making it more selective for producing one enantiomer of the epoxide.
The (ωB97XD/6-311G(d,p)/SCRF=dichloromethane) optimised geometries are shown below. The reaction centre is shown in a magenta box for the disfavoured (R) epoxide and in green for the favoured (S) epoxide (the hydrogens are not shown for clarity; if you want to see them, click on the image to get the 3D model).
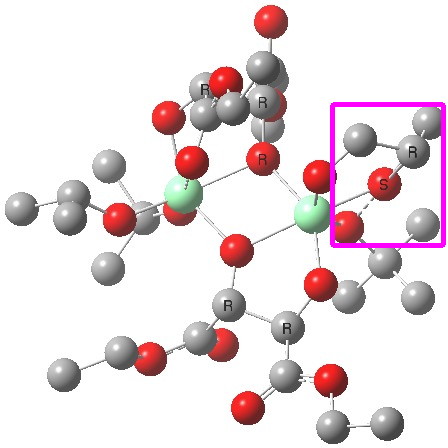 (R). Click for 3D. |
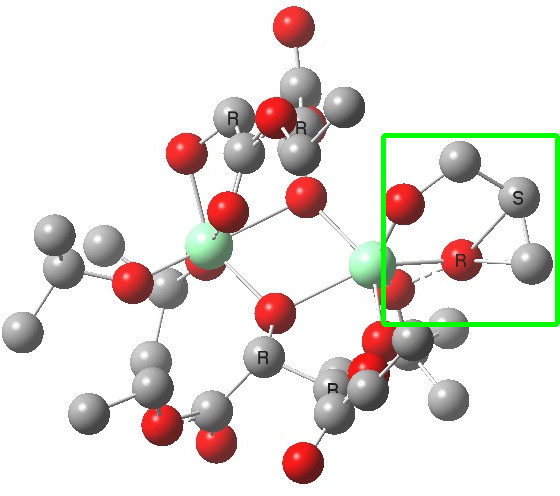 (S). Click for 3D |
You can see immediately that the biggest differences between the two occur in the bottom right corner. The t-butyl-O-O group folds in for (S) and this has a knock on effect on the two ester groups of the bottom right tartrate (the disposition of the tartrate on the top left is hardly changed). This folding is mediated by the hexa-coordination of the catalytic metal centre, together with dispersion interactions occurring to the t-butyl group, and this is helped by buttressing from the second Ti centre and its substituents.
The free energy difference ΔΔG298‡ favours the (S, FAIR DOI: 10.6084/m9.figshare.104675) for over the (R, FAIR DOI: 10.6084/m9.figshare.104625) by 3.0 kcal/mol. This free energy difference corresponds to an enantiomeric excess of >99%. In terms of attractive dispersion forces alone, (S) is favoured over (R) by -2.6 kcal/mol, and hence attractive dispersion seems to be the dominant term distinguishing between the two diastereomeric transition states. This aspect of non-covalent-interactions will be investigated in another post.
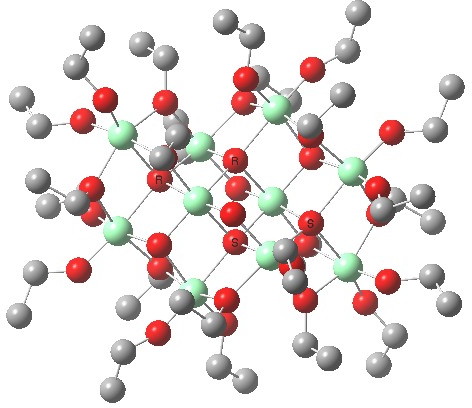
KOGYEK, a Ti oligomer.
One should however finally ask if this is the best model?
- Not all conformations have been explored in these models, although (S) was built from (R) as a template, so many features are the same. Nevertheless, further conformational exploration may be useful.
- Alkoxytitaniums are known to also form higher oligomers, such as the one shown above.[1]. If their concentration is significant, these too might be catalysing the reaction. Only computation would establish if they are capable of greater stereoselectivity/faster kinetics.
So we could end up with an answer that a number of oligomeric transition states are involved. But the one presented here, if not necessarily the most accurate or “best” model, seems good enough to form a template for further exploratory computation to see if the enantioselectivity of the reaction might be improved upon further.
References
- V.W. Day, T.A. Eberspacher, W.G. Klemperer, C.W. Park, and F.S. Rosenberg, "Solution structure elucidation of early transition metal polyoxoalkoxides using oxygen-17 NMR spectroscopy", Journal of the American Chemical Society, vol. 113, pp. 8190-8192, 1991. https://doi.org/10.1021/ja00021a068
Tags: catalysis, catalytic metal centre, Enantioselective, free energy difference, Reaction Mechanism, Sharpless epoxidation, t-butyl, This free energy difference, Tutorial material
[…] What they do not do is measure the attractive dispersion contributions to the model. I had suggested that differential dispersion contributions may be a (dominant?) factor in explaining why Sharpless […]
[…] full set, but felt it worth reporting two conformations which have lower energies than the ones I reported in this post. If I find any yet lower in energy, I will add a postscript […]