The 100th anniversary of G. N. Lewis’ famous electron pair theory of bonding is rapidly approaching in 2016 (DOI: 10.1021/ja02261a002). He set out a theory of bond types ranging from 1-6 electrons. The strongest bond recognized by this theory was the 6-electron triple bond, a good example of which occurs in dinitrogen, N2. In terms of valence electrons, nitrogen has an atomic configuration of 2s2, 2p3. Each atom has five electrons in total, some or all of which in principle could be used for forming bonds. An exploration of this motif across the entire periodic table is presented in part one of this blog.

Nitrogen is in the main group 15, and the element at the bottom of this group is Bismuth (also with the same atomic configuration). We can then move to the corresponding column of the transition series, this time occupying group 5. The first examplar in this set, Vanadium has an atomic configuration of 3d3, 4s2, again five valence electrons, but now utilizing the d- rather than the p-shell of valence atomic orbitals (AOs). The final forage across the period table would land us with Pr and Pa, which occupy the lanthanide and actinide series respectively, and which have atomic configurations of 4f3, 6s2 and 5f2, 6d1 and 7s2 respectively. You can now see the theme developing; how does the bonding develop between two atoms that between them have ten valence electrons occupying molecular orbitals constructed from s, and then either p, d or f atomic orbitals. The next in that series, g atomic orbitals, are thought unlikely to have any chemical significance in the presently known periodic table.
We are in fact going to study the diatomic molecule comprising two atoms of each element, and further we are going to protonate this species on one of these atoms resulting in the molecule HX2+. So let us start with the two systems HN2+ (Figure 1, 1a-1e) and HBi2+ (Figure 1, 2a-2e).

Figure 1. The molecular orbitals of HN2(+) and HBi2(+)
The two most stable valence molecular orbitals (MOs) for each system (1a and 2a) are the symmetric and antisymmetric combinations of (assumed pure) s-AOs, each populated with two electrons. For Bi (2a/2b) it is fairly clear that this bonding and anti-bonding combination cancel almost exactly. The bond order resulting from these four valence electrons is therefore close to zero. But N is in fact rather odder (and in part, the reason for protonating the systems was to tease out this oddity)! The apparently antibonding 2s-2s combination (1b) actually has electron density along the N-N bond, and the node occurs not along the bond, but at the actual nitrogen atom. So for N, the bonding and anti-bonding σ-bond combinations do not cancel, and the sum of these two may actually lead to a non-zero bond order.
With Bi, the next most stable MO results from the overlap of two 6p-AOs end on (2c); the anti-bonding combination of these AOs is in fact the 2e (with no occupying electrons). Result: bond order of +1, and this bond is called a σ-bond. The final MO shown (2d) is in fact one of a pair of MOs (only one of which is shown here), resulting from parallel overlap of two 6p-AOs. Result: bond order of +2, and we call these two p-π-bonds. The total bond order is +3, comprising 1 σ-bond and two p-π-bonds. No surprises here yet! For N, the relative order of the π- (1c) and the σ-bonds (1d) is swapped compared to Bi (which might be due to relativistic effects, see below), but one can again argue that these three orbitals together contribute 1 σ-bond and two p-π-bonds to the total bonding. So, to summarize, HBi2+ exhibits a classical triple Bi…Bi bond; HN2+ in contrast may actually exceed the bond order of +3, and a case could be made for arguing it is an abnormally strong bond (there is evidence that the N…N stretching frequency in the protonated species is significantly higher than the simple diatomic nitrogen gas).
Let us now move to the combination HV2+ (3) and HTa2+ (4, Figure 2). There are two major differences for V compared to N. Firstly, a 3d rather than 2p -AO is used for the bonding. Secondly, the 3d-AO is actually lower in energy than the 4s-AO, the reverse of the 2s/2p order for eg nitrogen. So what effect does this have on the resulting molecular orbitals?

Figure 2. Valence molecular orbitals for HV2(+) and HTa2(+). Click image for 3D of Delta orbital
The difference between N and V turns out to be spectacular, in several regards! The most stable MO (3a) now turns out to be composed of end-on overlaps of two 3d-AOs. There are in fact two of these orbitals (only one is shown in Figure 2), and together they form two 3d-π bonds. The next MO (3b) involves the end-on overlap of a 3dz2-AO, this time forming one 3d-σ-bond. Finally, the 4s-AOs get in on the act, forming now one bonding s-σ-bond (3c). So far, eight of the ten valence electrons have been consumed; two more to go. But now we have a problem. The next MO is formed by parallel overlap of two 3d-AOs (Figure 2, 3d), and in fact there is a pair of these combinations (again, only one is shown in the figure), which are in fact equal (degenerate) in energy. Because they are equal in energy, they must both be populated by an equal number of electrons, but since there are only two valence electrons left, we end up with one electron in each of these two orbitals, resulting in a triplet spin state. Exactly the same phenomenon is responsible for diatomic oxygen also adopting a triplet rather than singlet spin state. This parallel overlap of two 3d-AOs is said to form a 3d-δ-bond. The total bond order in molecule 3 therefore comprises two 3d-π-bonds, one 3d-σ-bond, one 4s-σ and two half 3d-δ-bonds, i.e. five in total and enforces a triplet spin state. So in the sense of formal bond order, the V-V bond in 3 is greater (and perhaps even stronger) than in 1. What a difference from nitrogen!
How about Ta? This has an atomic electronic configuration of 5d3, 6s2. The molecular orbitals are shown in Figure 2 (right). The significant difference in this region of the periodic table is that so-called relativistic effects start to influence the relative ordering of the atomic orbitals. This so-called relativistic contraction impacts upon s-AOs far more than p, or d or f. Thus orbital 4a (Figure 2, right) comprising a symmetric combination of Ta 5s-AOs is more compact than the corresponding V orbital (3c), and relatively more stable. Next come the end-on overlaps of two 5d-AOs (4b), of which there are two (degenerate) combinations (only one is shown in Figure 2). MOs 4c and 4d are again best described as originating from the 6s Ta AO, but with significant contributions from the 5d-AOs (sd-hybrids if you will). Significantly, the relativistic effect means that the δ-bond formed by parallel overlap of two 5d-AOs (4e) is left vacant. Thus the bonding in 4 comprises an 6s-σ-bond, two 5d-π-bonds, and two sd-σ-bonds (one of which does look rather anaemic) but NO 5d-δ-bond! The consequences of the relativistic effect is the relegation of the δ-bond to unoccupied status and the formation of a singlet rather than a triplet spin ground state.
Given the big differences in bonding which occur upon changing a 2p-valence atomic orbital to 3-5d-AOs, one wonders what will happen with 4-5f-AOs? A π-bond can be formed by the parallel overlap of two p-AOs, or end-on overlap of two d-AOs. A δ-bond can be formed by the parallel overlap of two d-AOs. Could then a δ-bond also be formed by the end-on overlap of two f-AOs? Would a φ-bond be formed by the parallel overlap of two f-AOs? The latter might look something like that shown in Figure 3, shown in two different orientations (these diagrams were obtained by inspecting the unfilled MOs in the V/Ta examples shown here; notice that although the φ bond appears to be bonding, the system has chosen not to occupy it with any electrons!).
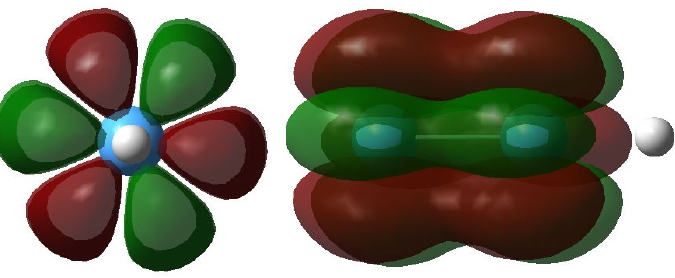 Figure 3. Two views of a φ bonding MO. Click image for 3D |
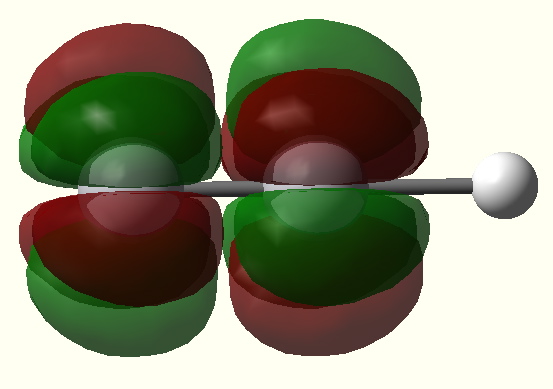 Figure 4. A φ* antibonding MO. Click image for 3D |
This blog will end by posing the question “can any molecule be devised which supports one or more φ-bonds”, or will the relativistic contraction always scupper such efforts by depriving such bonds of electrons (e.g. Ta above)? Are the systems reported in DOI: 10.1021/ja067281g examples of a 5f-φ bond for uranium (the claim is made in a very low key manner)? This will be investigated in the follow up to this post!
(For serious geeks/computational chemists only, N was computed at the B3LYP/6-31G(d) level, V at the ROHF/6-31G(d) level, and Bi/Ta at a triple-ζ-pseudopotential level (which incorporates some of the relativistic effects).
Tags: chemical significance, diatomic nitrogen gas, energy, Interesting chemistry, pence, stable MO, The 100th anniversary of G. N. Lewis' famous electron pair theory of bonding, Vanadium
Thank you for this very interesting article
This is a really useful article. Chemistry is a personal interest of mine and i find your posts both enlightening and useful.
[…] taking a look at that question, I note first a previous post in which I speculate upon the ultimate chemical bond, a 5f-φ bond between two uranium atoms […]