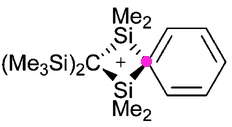
Charges in chemistry, like the grin on Lewis Carroll’s cat, can be mysterious creatures. Take for example the following structure, reported by Paul Lickiss and co-workers (DOI: 10.1039/b513203g).
A student of chemistry might be wondering what is going on, since this representation seems to “break the rules”. Thus there is a clear-cut pentavalent carbon atom, but even more mysteriously, there is a positive charge that seems to be floating uncertainly (much like Carroll’s Cheshire cat). Another Lewis famously introduced the concept of the covalent electron pair bond in 1916, and ever since then we tend to represent these types of bond with (straight) lines. If this convention is adhered to rigidly, then the carbon highlighted with the purple dot would have five lines to it, 10 electrons, and therefore in violation of the octet rule for main group elements. Nowadays however, a line between two atoms is not necessarily interpreted as a Lewis structure, but more simply representing a connection to be used in a connection table for indexing and searching the structure. So what IS the valency of this carbon, and where IS that charge located?
One starts by converting the above representation into more formally correct Lewis, or valence-bond structures.
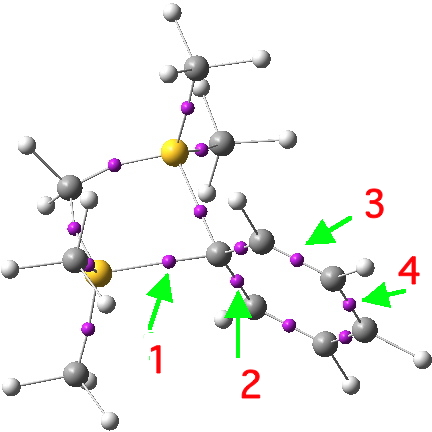
These structures (there are more, but they are related by symmetry to those shown above) are bound, by the rules, to locate the bonds exactly, and hence allow one to infer where the charge is. The latter two emerge as different resonance forms of what we call Wheland intermediates. The former is the silicon equivalent of a tertiary carbocation. Quantum mechanics now tells us which of these (if any) is the most realistic. To do this, I invoke the ELF (electron localisation function) method, which identifies so-called synaptic basins in the function, and how much electron density is contained in each (there are of course many other ways of partitioning the electrons).
Basin 1 has 1.51, basin 2 has 2.39, basin 3 has 2.84 and basin 4 has 2.65e. Let us discuss the significance of these.
- Basins 1+2 (+ their symmetric equivalent) together contain 3.02 + 4.78 = 7.8e. Thus this carbon definitely is not hypervalent, since its octet is pretty much satisfied! But notice that this carbon is not a conventional so-called sp3 hybridized carbon, which has four equal two-electron bonds. This one has two bonds with significantly less than two electrons, and two with significantly more! A most unusual 4-coordinate carbon. Bond 1 has a Wiberg bond index of 0.48 and bond 2 is 1.29.
- By the same process, each Si atom integrates to 7.72e. If either were to be a silacation, that would imply only 6 electrons, which is clearly not the case for either Si.
- How about the ortho, meta and para carbons of the phenyl ring? These are respectively 7.39, 7.64 and 7.44e. These are definitely a bit low, and taken together they constitute the equivalent of a six-valence electron carbocation. So it looks as if we have found our positive charge, which is delocalized on the phenyl ring in the manner of a Wheland intermediate (with more of the +ve charge on the o/p positions).
Well, if this species is really a Wheland intermediate in which the cyclic conjugation of π-electrons is disrupted, the phenyl ring should not be aromatic. In fact, it turns out this ring IS recognisably (if not highly) aromatic. Its NICS(1) index value is -8.3ppm (benzene is ~-11 on the same scale). Exactly the same phenomenon was found for the supposed Wheland intermediate (which in fact turned out to be a transition state) identified as the mechanism of nitrosation of benzene using CF3COONO. Can all these disparate properties be reconciled?
Yet another way of looking at what is happening in this molecule is Natural bond orbital analysis (NBO). I have previously used this technique to probe the structure of DNA, and for identifying unexpected anomeric effects (amongst others). Applied to this system, it reveals four donor-acceptor interaction energies E(2), each of ~ 10.5 kcal/mol, between the four permutations of e.g. bond 1 acting as the donor, and bond 3 acting as an acceptor, a σSi-C/π*C-C interaction. The value of E(2) corresponds to almost a full anomeric effect (these tend to be ~15 kcal/mol if the donor is a O lone pair and the acceptor a C-O bond), and there are four of them after all! This particular conjugation is the one that makes the phenyl ring retain much of its aromaticity, i.e. having its cake and eating it.
Notice that individually, each of the effects I have described above is actually borrowed from fairly conventional introductory level organic chemistry (Lewis structures, the octet rule, cation stability, aromaticity, stereoelectronic/anomeric effects), and it shows how a combination of these in a single molecule can result in quite unusual properties.
Tags: Lewis Carroll, Tutorial material

[…] now called σ-π conjugation, and which used to be called hyperconjugation (it also resembles the conjugation of a Si-C bond with a phenyl ring in the Wheland […]
[…] There is one other aspect I want to explore. In the Meisenheimer intermediate, the cyclic conjugation and hence the aromaticity of the original aryl ring is (at least partially) interrupted. But what of the concerted transition state; must it too loose the original aromaticity? In the structure diagram drawn at the top of this post, I hinted it might not! A NICS(0) probe place at the QTAIM-determined centroid of the aryl ring (X=Y=H, Nu=Cl) indicates a value of -9.0[10] (benzene itself is about -10 ppm), indicating relatively little cyclic conjugation is actually lost in the transition state. The nature of the molecular orbital confirms this. Shown below is the most stable of the three aromatic π-MOs, again resembling that of benzene very closely and the two C-Cl partially formed bonds participate fully in this conjugation. So we might call this strongly hyper-conjugated aromaticity. […]