One of my chemical heroes is William Perkin, who in 1856 famously (and accidentally) made the dye mauveine as an 18 year old whilst a student of August von Hofmann, the founder of the Royal College of Chemistry (at what is now Imperial College London). Perkin went on to found the British synthetic dyestuffs and perfumeries industries. The photo below shows Charles Rees, who was for many years the Hofmann professor of organic chemistry at the very same institute as Perkin and Hofmann himself, wearing his mauveine tie. A colleague, who is about to give a talk on mauveine, asked if I knew why it was, well so very mauve. It is a tad bright for today’s tastes!

Charles Rees, wearing a bow tie dyed with (Perkin original) mauveine and holding a journal named after Perkin.
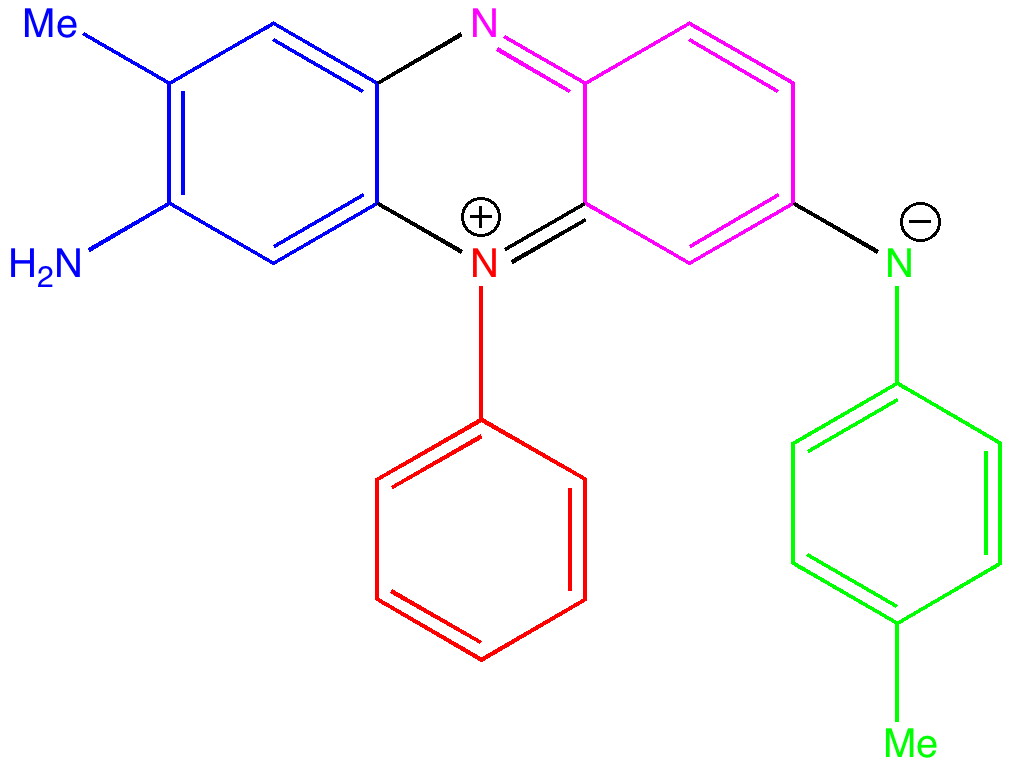
The first thing to note about mauveine is that it is not a single compound; actual samples can contain up to 13 different forms! These all vary in the number of methyl groups present which range from none up to four, in various positions. These compounds all have absorption maxima λmax in the range 540-550nm, the colour of purple. The structure of one of these, known as mauveine A, is shown below.

Mauveine A. Click to load 3D
This has several noteworthy aspects.
- The visible (right hand side) part of the spectrum is very monochromatic, with λmax ~440nm. In other words, mauveine has a pure and intense colour.
- This λmax is hardly affected by the presence of the counterion.
- The electronic transition responsible for this band is a simple HOMO (highest-occupied-molecular-orbital) to LUMO (lowest-unoccupied-molecular-orbital) excitation of an electron.
- These orbitals are shown below.
LUMO HOMO 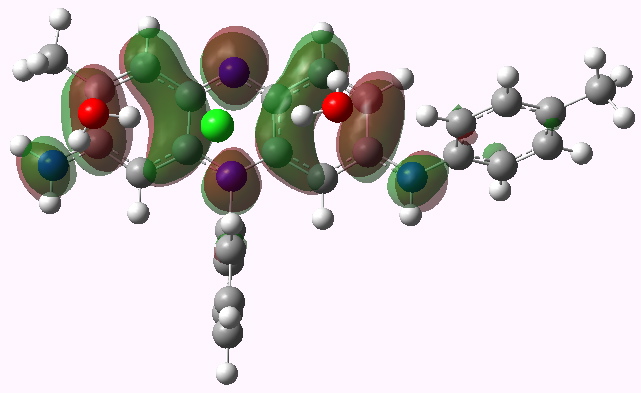
Mauveine A. LUMO. Click for 3D
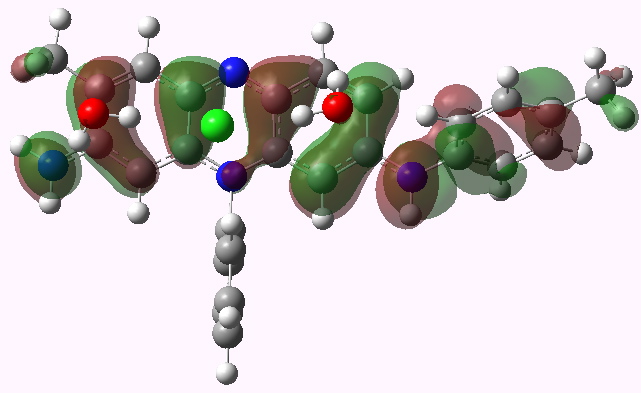
Mauveine A. HOMO. Click for 3D
- Note how the excitation involves the central region of the molecule, and one of the pendant aryl groups, but not the other. One might presume that tuning the colour would only work if changes are made to the first of these aryl groups.
- There is a real mystery about the calculated value of λmax, which differs from the observed value by about 100nm (the wrong colour, making mauveine orange rather than purple). Normally, this sort of time dependent density functional theory has errors no greater than 15-20nm. The calculated value of λmax is not sensitive to the basis set, or the presence or not of the counter ion and solvent. Clearly, a discrepancy of this magnitude must have some other explanation. Watch this space!
So this post ends with a bit of a mystery. The fanciest most modern computational theory gets the colour of mauveine wrong by ~100nm. Why?
Tags: August von Hofmann, Charles Rees, chemical heroes, chiroptical, colour, founder, Historical, Hofmann, HOMO, Imperial College, Imperial College London, LUMO, Mauveine, Perkin, professor of organic chemistry, purple, Rees, Royal College of Chemistry, William Perkin
Is there experimental evidence for ion-pairing? Mauveine seems to retain its color despite the anion employed (chloride, acetate, sulfate, etc.) and it is difficult for me to believe that all anions would coordinate in the same manner. Because there is no chloride character in either the HOMO or LUMO, I think we can assume its effect will be electrostatic. The more localized nature of the LUMO means that it will be raised higher in energy relative to the HOMO (compared to a model w/o chloride), and thus the transition would be higher in energy. This effect could be worth a few hundred meV, so I removed the chloride / two methanols and compute, without reoptimization, the first excited state at wB7XD/6-31G(d,p). The transition energy of 530nm seems quite close to experiment but one would have to test this with a better basis set and checking for significant structural reorganization in the absence of the chloride / methanols.
My apologies, one should be more careful blogging before morning coffee!
(i) I did not mean to undermine your work – I missed that you had tested this hypothesis yourself. That being said, with both the 6-31G(d,p) and 6-311G(d,p) basis sets I find a large shift from 450nm to ~740nm (see point ii for different # than quoted earlier) for the cation w/o anion and explicit methanols. Could you elaborate on what calculations led you to conclude that the explicit Cl / MeOHs didn’t shift lambda max much?
(ii) In testing new input creation software for a colleague, I seem to have stumbled across a bug that causes it to ignore user-defined charge/multiplicity. This may be quite fortuitous. The data I listed in my previous post is for the neutral radical, and the value of 530-540nm seems to be independent of basis now that a few other calculations have finished. Is enough known about the electrochemistry of Mauveine to say whether the neutral radical is plausible?
Richard,
I had indeed earlier done a calculation on the pure cation rather than the ion-pair, and this came up with an (approximately) HOMO-LUMO excitation energy corresponding to ~437 nm (see DOI: 10042/to-7340) which is very similar to the ~440nm obtained for the full system. From which I had concluded that the electrostatic effect was surprisingly small, and that it hardly changed the HOMO-LUMO gap. This for the geometry of the cation fully optimized without the chloride. Your estimate based on removing the chloride and two solvent molecules, but leaving the rest of the geometry unchanged does not, as you say, take into account structural reorganisation, although in fact it does appear to be fairly small (< 0.05Å). Also, the excitation energies I quote are derived from time-dependent DFT theory, and not simply the HOMO-LUMO band gap, which I think you used to obtain a transition energy of ~530nm. In general, DFT (as opposed to HF) gives quite poor HOMO-LUMO band gaps (often numerically too small, resulting in excitations which are far too low in energy, and hence wavelengths which are too high). I am certainly no expert on TD-DFT, but where it is used to e.g. predict ECD spectra, it tends to get λmax for the CD transition to within ~15nm or so. Or, to put it another way, I have never seen it to be out by 100nm for ECD transitions. There is always a first time I suppose. As to your second point, yes, if you start with a radical, and excite that, your excitation energies will indeed be much lower than had you started with a cation. So I think 740nm for a radical is to be expected. Whether one can reduce the mauveine cation to a radical (using e.g. cyclic-voltametry) is a most interesting question. I have not carried out a literature search for this, but perhaps it might give another clue as to why mauveine is mauve, and not orange. As for the basis, 6-311G(d,p) and the better 6-311++G(d,p) hardly altered the results, as you suggest. About the only variable left is to explore the functional. As it happens, functionals which include long range correlation effects (CAM-B3LYP) are said to be better at getting excitation energies well reproduced. ωB97XD also has such a long range term, and in our hands has given slightly better results than CAM-B3LYP (or so we had thought until this result came up).
As a follow up to my earlier response, a quick check of CAS suggests nothing under the search term mauveine cyclic voltametry and only one irrelevant hit under mauveine reduction potential. The way forward might be to identify a system which is well characterised in this regard, and see if the methods I used in this post at least reproduce that system well.
I don’t know if it will work but a relatively simple pH-dependent colour changing system like Congo Red might be a nice test.
I think virtually any intense nitrogen-containing chromophore might do the trick (Congo red is not a quaternary nitrogen cation, so it is a little different), but it would be worth selecting one that has as much structural similarly to mauevine as possible, and one where the 1-electron reduction potential is also known (with or without solvation).
Another update to my earlier notes. I have repeated the TD-DFT calculation with another functional (CAM-B3LYP), getting the same results (λmax ~440nm). Not too sensitive to counter-ion, solvent, basis set or functional then.
About the only thing I can think of is that the system aggregates/stacks in some way.
[…] lazuli- the colour of ultramarine. My colleague Bill Griffith has again come up with another colour challenge: that of the ancient semi-precious stone Lapis Lazuli, mined […]
[…] just as with mauveine, a mystery remains. The colour of Monastral blue is not monochromatic, in that it appears to be […]
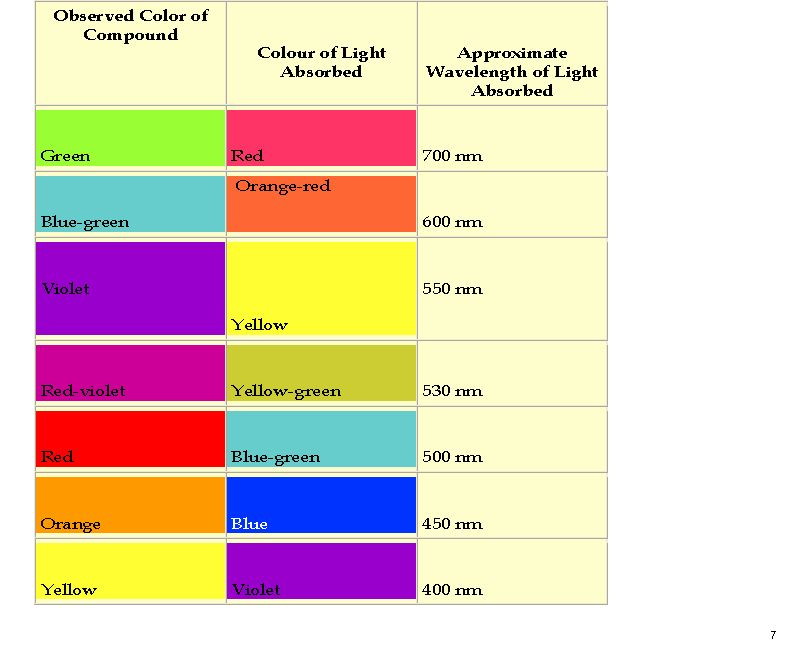
Here is a colour table which makes it easier to relate λmax to the actual observed colour.
I am still trying to find a model which will explain why mauveine is mauve (purple). In other words, why λmax is 540nm. Perhaps if one deprotonates mauveine to form what is called the free base?

The calculated spectrum is shown below, for which λmax is 481nm. Still not right!
[…] previous post on the topic of mauveine left the outcome dangling. Put simply, λmax is measured at about 549nm for mauveine A, but was calculated at about 440nm […]
Hello, bit of an odd question: do you happen to know an approximate value of a piece of fabric which would have been dyed with the original mauveine (or the value of Prof Charles Rees bow tie). I would love to know if such an item would be valued as a collectible or bought at an antiques auction.
Thank you very much for your time
The short answer is no. I do not believe any such item has ever come up for sale!
Posted on behalf of Stefan Grimme
======================
Dear Henry,
A colleague pointed me to your page http://www.ch.imperial.ac.uk/rzepa/blog/?p=3507 asking about this 100 nm failure and possible reasons (because I have some experience in theoretical UV/CD). Here is my opinion on that:
1. comparisons theory-exp. should be done on a linear eV or cm-1 scale but not in nm (which is non-linear). The difference from 450 nm to 550 nm corresponds to an error of only 0.45 eV.
2. Comparisons of vertical excitation energies with exp. band maxima can easily introduce errors of 0.2 eV.
3. Your solvation model is crude and may add another uncertainty of about 0.1 eV.
4. If you add all this you arrive at a more realistic 0.2-0.3 eV TDDFT error which we also observe for smaller chromophore benchmarks compared to e.g. high-level WFT results.
5. if you convert 0.2 eV into 5 kcal/mol you will find that this is not an uncommon DFT error also for e.g. a ground state reaction energy of about 50 kcal/mol. So in summary its not special or surprising at all (its our eye which is very sensitive).
Cheers!
Stefan
—
____________________________________________________________
Prof. Dr. Stefan Grimme (grimme@thch.uni-bonn.de)
Chair of Theoretical Chemistry
Mulliken Center for Theoretical Chemistry
University of Bonn
Beringstr. 4, D-53115 Bonn, Germany
Inspired by Stefan’s suggestions (posted above), and mindful that DFT reparametrisations can “correct” in a non-linear way, I repeated the UV-Vis TD-DFT prediction for mauveine, using exactly the same geometry as was used in the model above, but using a “new generation” of functional, MN12L (DOI: 10.6084/m9.figshare.1148892 ).
Now the error reduces from ~100nm to ~25nm, which is pretty good agreement. It seems that careful parametrisation of DFT methods can probably achieve better and better reproduction of electronic spectra in this region.