Reactions in cavities can adopt quite different characteristics from those in solvents. Thus first example of the catalysis of the Diels-Alder reaction inside an organic scaffold was reported by Endo, Koike, Sawaki, Hayashida, Masuda, and Aoyama[cite]10.1021/ja964198s[/cite], where the reaction shown below is speeded up very greatly in the presence of a crystalline lattice of the anthracene derivative shown below.
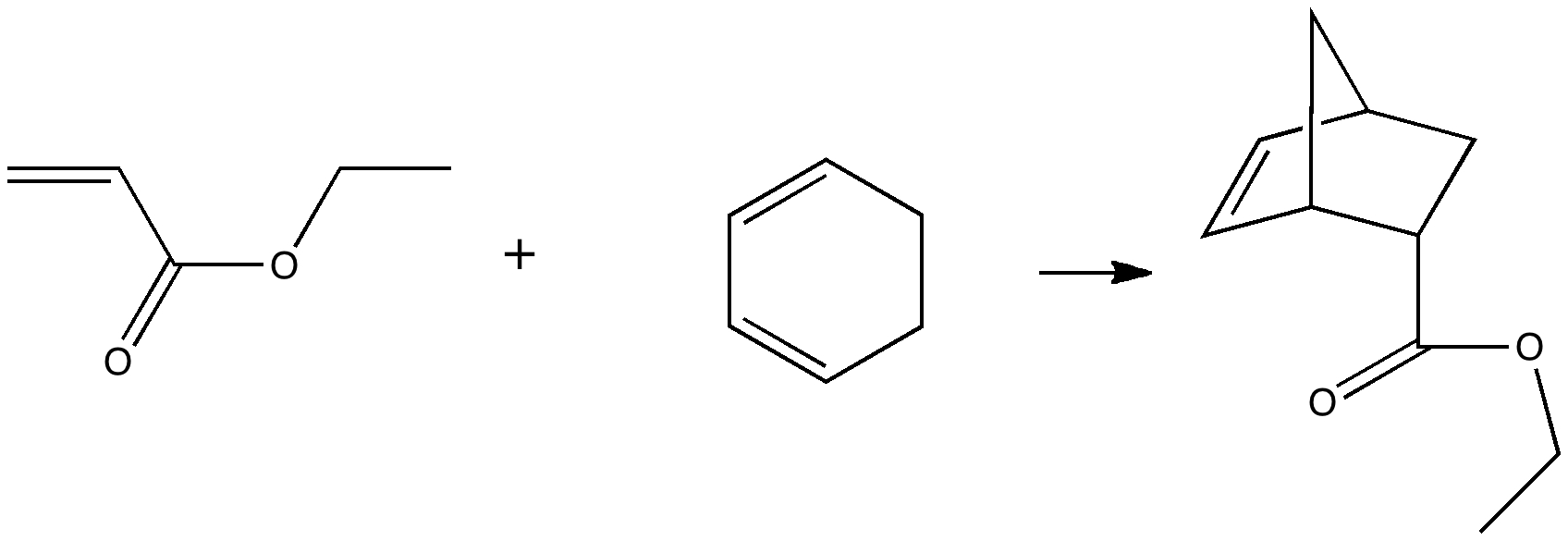 A Diels-Alder reaction. Click for animation. |
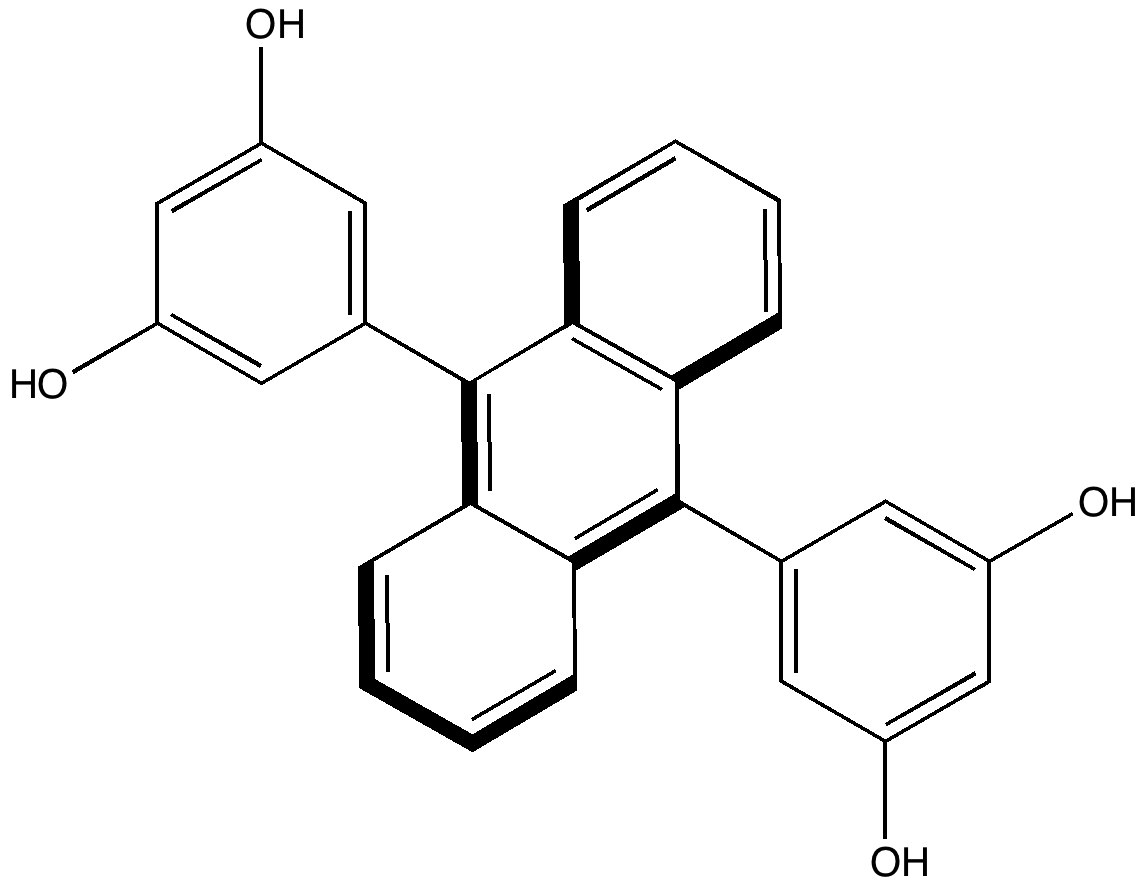 Organic scaffold based on an anthracene derivative. Click for crystal structure. |
Its difficult to be precise about how much faster, since the kinetics depend on reorganisation of the scaffold, the actual reaction kinetics, and diffusion of the products in and out of the cavity. It does however mean that a poor solution reaction (reflux, many hours, modest yield) can be accomplished in an hour or so at room temperature in high yield.
Some idea of what is going on can be probed using calculation. Because the host and the guest interact though van der Waals or dispersion forces, a new breed of density functional theory which takes these into account is used (ωB97XD). The basic assemblage comprises the reactants shown below, enclosed in a cage formed by four of the anthracene units. A total of 236 atoms. This is a pretty challenging size for a full-blown quantum mechanical calculation. Here, its been done using a reasonable basis set, 6-31G(d) and with a continuum solvation model applied (dichloromethane). If you are interested in this sort of thing, that is 2292 basis functions. I started the calculations in mid September, and its taken more than six weeks to optimise (on 8-processor computers).
Firstly, the results for a control calculation in dichloromethane. The energies of activation of the two isolated reactants coming together at the transition state are calculated as:
ΔG298 29.5, ΔH 15.5, T.ΔS -13.98 kcal mol-1
(ΔS -46.9 cal K-1mol-1)
which are of course the various contributions to the equation ΔG = ΔH – T.ΔS. Note in particular how the last term increases the free energy barrier by ~14 kcal mol-1! Using the equation
Ln k/T = 23.76 – ΔG/RT
one can estimate a rate constant of ~4 x 10-6 hour-1 at 298K (i.e. very slow at room temperatures). If the unfavourable -T.ΔS term is ignored (ΔG = ΔH), the rate constant increases to ~9 x 104 hour-1 at 298K (i.e. fast), quite a difference. What about the values when the reactants and transition state are surrounded by the host?
ΔG298 20.0, ΔH 16.5, T.ΔS -3.49 kcal mol-1
(ΔS -11.7 cal K-1 mol-1)
The key difference is that the last term is now much smaller, this reduces the free energy of activation and the estimated rate constant at 298K is now ~ 0.01 s-1 (42.5 hour-1). This magnitude of rate constant corresponds to a reasonably fast reaction at room temperatures.
Transition state for Diels Alder inside a cavity. Click for 3D.
This post demonstrates that the fascinating area of supermolecular chemistry can be just as amenable to computational exploration as the more conventional reaction.
Tags: animation, catalysis, free energy, free energy barrier, G/RT, Interesting chemistry, Organic scaffold, pericyclic
[…] I tend to think probably not (? rather than !). But do decide for yourselves. Archived as http://www.webcitation.org/5rpkn2Z5S on 08/08/2010. See also this post. […]
[…] waters (see DOI: 10.1039/C0CC04023A for an example if its use for a large molecule, or indeed this post). In truth, this combination of characteristics in a model has only recently become possible for a […]
[…] As transition states go, it is akin to asking whether the two bonds that form in e.g. a Diels Alder cycloaddition reaction form at the same rate (a concerted synchronous reaction) or at different rates (a concerted […]
Thanks a lot for the very nice notes. Actually I have some questions related to this topic and specifically the computational part. Firstly, the entropy term of the complex looks more favorable than the free which is unexpected due to loss of degree of freedom in the complex form.
Then, I do not know if optimized (locate) the transition state inside the cavity with OPT=TS, or you fixed the transition state structure and then optimized the rest.
Thanks again
Best Regards.
We are dealing here with entropies of activation, not absolute entropies. That for the free complex is very negative, which arises from the loss of degrees of freedom of the two separated reactants when they come together to form a transition state.
In the cavity, the two reactants do not have these degrees of freedom from the start, and so the activation entropy is much smaller when they form the transition state.
Yes, the transition state was fully located inside the cavity. There are no constraints. Without doing this, it would not be possible to do a meaningful vibrational analysis (the six degrees of translational and rotational freedom would not be zero).
Thank you for you fast reply and the useful comments. Actually, I still have a question about locating the TS inside a cavity. I am trying to find the TS inside macrocyclic host and I am using TS keyword, the problem is: I start with TS geometry as the free TS and after several optimizations steps I see the TS goes either to the Products or the Reactants.
I use this keywords:
#P wb97xd/6-31G* opt=(cartesian,calcfc,ts,maxcycle=1000,noeigentest) freq
Is there other keyword to be added, or another option to be used.
Thanks again.
Best Regards
Khaleel
The trick is to reduce the first derivatives of your starting point down to close to zero everywhere except your approximate reaction coordinates. For a cycloaddition, you would use opt(modredundant) and then constrain just the two bonds that are forming in the transition state (to about 2.2Å each). Run this until your RMS gradient norm is < 0.002 (if possible). This may take a long time! Only then would you put that geometry into an optimisation with the keywords you used above. For a large system (> 200 atoms) this too may take a while! For really difficult systems, I sometimes have to replace calcfc with calcall (but not for systems with 200 atoms).
Hope this helps.