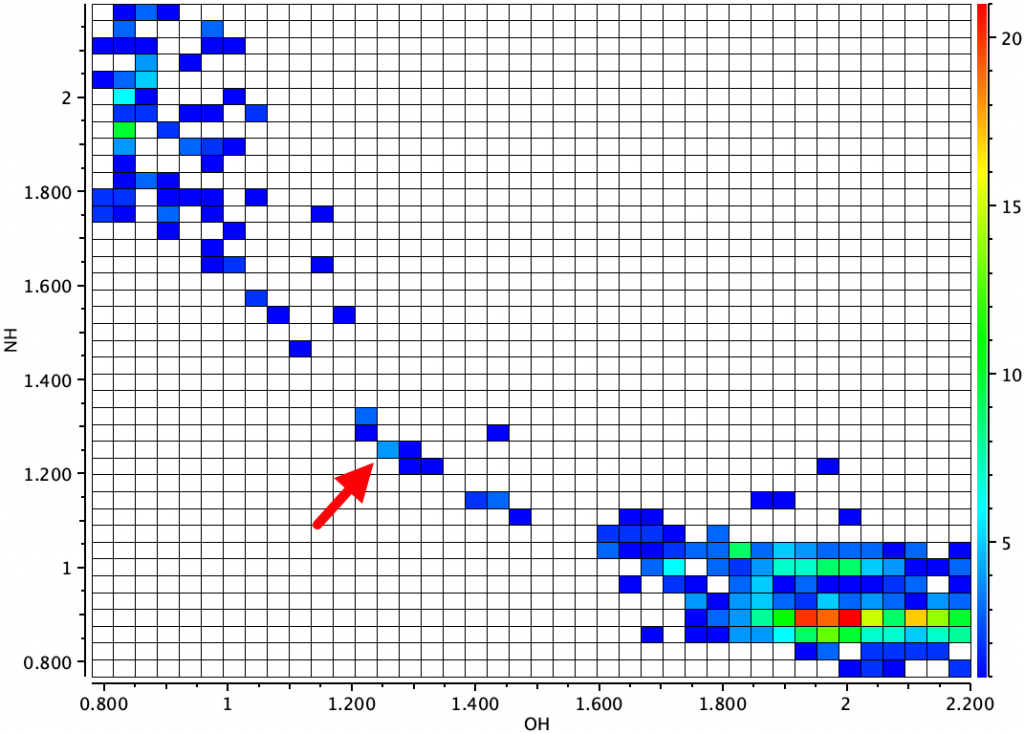
Proton transfers are amongst the most common of all chemical reactions. They are often thought of as “trivial” and even may not feature in many mechanistic schemes, other than perhaps the notation “PT”. The types with the lowest energy barriers for transfer often involve heteroatoms such as N and O, and the conventional transition state might be supposed to be when the proton is located at about the half way distance between the two heteroatoms. This should be the energy high point between the two positions for the proton. But what if a crystal structure is determined with the proton in exactly this position? Well, the first hypothesis is that using X-rays as the diffracting radiation is unreliable, because protons scatter x-rays very poorly. Then a more arduous neutron diffraction study is sometimes undertaken, which is generally assumed to be more reliable in determining the position of the proton. Just such a study was undertaken for the structure shown below (RAKQOJ)[1], dataDOI: 10.5517/cc57db3 for the 80K determination. The substituents had been selected to try to maximise the symmetry of the O…H…N motif via pKa tuning (for another tuning attempt, see this blog). The more general landscape this molecule fits into[2] is shown below:
The results obtained for the position of the proton for RAKQOJ were fascinating. They were very dependent on the temperature of the crystal! At room temperatures (using X-rays), the proton was measured as 1.09Å from the oxygen and 1.47Å from the nitrogen (neutral form above). At 20K, the OH distance was 1.309Å and the HN 1.206Å (~ionic form above). Indeed, the very title of this article is First O-H-N Hydrogen Bond with a Centered Proton Obtained by Thermally Induced Proton Migration. The authors give a number of reasons for this behaviour (their ref 17[1] and also[2]), but one they do not mention is thermally induced changes in the dielectric constant of the crystal with temperature, given that in one position for the proton the molecule is ionic and in the other neutral. So I decided to model the system as a function of solvent. In this model, the solvent dielectric is used to approximate the crystal dielectric. My first choice of energy function is to compute geometries using the B3LYP+GD3BJ/Def2=TZVPP/SCRF=solvent method to see what might emerge and as a possible prelude to trying other functionals. FAIR data for these calculations are collected at DOI: 10.14469/hpc/10368.
| Solvent | ε | ΔG298 for O…HN | rO…H | rHN | ΔG298 for OH…N | rOH | rH…N | ΔG298 TS (PT) |
rOH | rHN |
|---|---|---|---|---|---|---|---|---|---|---|
| Water | 78.4 | -2893.387188 -2893.334325♠ |
1.4913 | 1.0827 | -2893.386705 -2893.334333♠ |
1.0364 | 1.5696 | -2893.387668 -2893.336183♠ |
1.1852 | 1.2899 |
| Dichloro methane |
8.9 | -2893.385173 | 1.4566 | 1.0945 | -2893.385662 | 1.0309 | 1.5878 | -2893.386022 | 1.2072 | 1.2642 |
| Chloroform | 4.7 | -2893.382254 | 1.4227 | 1.1082 | -2893.384514 | 1.0261 | 1.6049 | -2893.384773 | 1.2321 | 1.2388 |
| Dibutyl ether | 3.1 | -2893.380813 | 1.3778 | 1.1302 | -2893.383511 | 1.0213 | 1.6235 | -2893.382918 | 1.2667 | 1.2078 |
| Toluene | 2.4 | -2893.379752 | 1.3248 | 1.1635 | -2893.382915 | 1.0178 | 1.6385 | -2893.379773 | 1.2851 | 1.1934 |
| Gas phase | 0 | n/a | -2893.377949 | 1.0009 | 1.7387 | n/a | ||||
| Expt (RT) [1] |
? | n/a | 1.09 | 1.47 | n/a | |||||
| Expt (20K) [1] |
? | n/a | 1.309 | 1.206 | n/a | |||||
♠ At 20K
Results:
- The geometries for each model are obtained by minimising the total energy of the system as a function of the 3N-6 geometric variables (coordinates).
- The geometries show that for all solvents, TWO minima in the total energy are obtained, one for the ionic and one for the neutral form. This is called a double-well energy potential. Even a non-polar solvent such as toluene produces a solvation energy of ~3.1 kcal/mol compared to the gas phase, which is sufficient to induce a double-well potential.
- Without solvent (gas phase), only the neutral geometry is obtained.
- In the most polar solvent water, the double well potential looks like this:
The ionic well is about 0.4 kcal/mol lower in total energy (and ~0.3 kcal/mol in free energy, see table above) than the neutral form, with a barrier connecting neutral to ionic only 1.0 kcal/mol. A transition state + intrinsic reaction coordinate (IRC) can be easily located on this total energy potential, confirming the double-well form. - When free energies ΔG are computed, which include thermal effects such as entropy and zero-point energy, the transition state emerges as 0.3 kcal/mol less than the total energy of the ionic form (red entries, Table). In effect, the free energy potential surface is INVERTED compared to the total energy surface and the “transition state” becomes the lowest point on the energy surface. So this point is a minimum in the free energy but a maximum in the total energy, the result of adding thermal effects to the total energy.
- In dichloromethane, the free energy of the neutral form is now lower by 0.3 kcal/mol than the ionic form. The OH bond is starting to get shorter and the NH one longer. The transition state is now 0.22 kcal/mol lower than the neutral form. With chloroform, the OH and HN bonds have become ~equal in length, the proton is symmetrically disposed.
- By the time dibutyl ether as solvent is reached, the transition state is no longer lower in ΔG than the neutral form, moving on to being 2.0 kcal/mol higher for toluene. So as the solvent polarity decreases, we see a change in the potential from a single well in ΔG, in which the proton is centred, to a very asymmetric well in which the proton is attached to the oxygen.
- Can we match the observed neutron diffraction results to the calculations? As the temperature decreases, the neutron diffraction shows the start of proton transfer from oxygen to nitrogen to form an ionic species. The calculations show that this can be modelled by an increase in the effective dielectric constant of the medium. The computed “transition state” for proton transfer somewhere between dibutyl ether and toluene (as a dielectric media) emerges as approximately the best model for the structure of this species. At this dielectric, the calculated ΔG is no longer quite the lowest free energy point in the potential. This might be due to the many approximations used in this model such as minimisation of total energy, the partition function method used to calculate entropy, the nature of the DFT functional, the continuum solvation model, the basis set, etc.
Conclusions:
These results were obtained with the approximation that minimising the total molecular energy produces a computed geometry that can be compared to the experimental neutron diffraction structures. But can one do better? Obtaining molecular geometries by minimising the computed free energies would be non-trivial. Firstly, minimisation would depend on availability of first derivatives of the energy function with respect to coordinates, in this case ΔG. These are not available for any DFT codes. The result would itself be temperature dependent (as indeed are the experimental results shown above). Furthermore, ΔG is computed from normal vibrational modes and these are only appropriate when the first derivatives of the function are zero, at which point the so-called six rotations and translations of the molecule in free space also have zero energy. So we need vibrations to compute derivatives, but we need derivatives to compute vibrations in this classical approach.
It would be great for example if the approximate model of the potential for a hydrogen transfer used above as based on minimising total energies for derivatives could be checked against a model based on geometries optimised using free energies instead. Such procedures do exist,[3] using molecular dynamics trajectory methods.
This post has DOI: 10.14469/hpc/10382 [4]
References
- T. Steiner, I. Majerz, and C.C. Wilson, "First O−H−N Hydrogen Bond with a Centered Proton Obtained by Thermally Induced Proton Migration", Angewandte Chemie International Edition, vol. 40, pp. 2651-2654, 2001. https://doi.org/10.1002/1521-3773(20010716)40:14<2651::aid-anie2651>3.0.co;2-2
- I. Majerz, and M.J. Gutmann, "Mechanism of proton transfer in the strong OHN intermolecular hydrogen bond", RSC Advances, vol. 1, pp. 219, 2011. https://doi.org/10.1039/c1ra00219h
- M. Higashi, S. Hayashi, and S. Kato, "Geometry optimization based on linear response free energy with quantum mechanical/molecular mechanical method: Applications to Menshutkin-type and Claisen rearrangement reactions in aqueous solution", The Journal of Chemical Physics, vol. 126, 2007. https://doi.org/10.1063/1.2715941
- H. Rzepa, "Geometries of proton transfers: modelled using total energy or free energy?", 2022. https://doi.org/10.14469/hpc/10368
Very insightful article. How about the role of tunneling effect in this particular problem?
Dear Latte,
Tunnelling occurs through a potential energy barrier. If there is no barrier, then no tunnelling can occur. In this case, a free energy barrier.
Just wonder how difficult it was to find the TS, I presumed you first used scans, then calcall and a small stepwise for the actual TS, but are other keywords you can recommend, especially for proton transfer?
Andrew,
Thanks for the comment. To answer your questions
1. I do not recollect any particular difficulties. You can always see the keywords used by going to the results at https://doi.org/10.14469/hpc/10368 to find out.
2. Scans are rarely used for simple proton transfers. I normally place the proton at approximately the mid point. I will then constrain the two X-H lengths using opt(modredundant) to eliminate forces in the rest of the molecule. Normally, calcfc, and recalcfc=5 or so will then do the trick to refine the final position of the proton. Only if that fails is calcall used.
3. The other keyword that is useful is integral=(acc2e=14,grid=superfinegrid,noxctest) The higher than normal integral accuracy ensures that the CPHF section converges quickly, and the extra large quadrature grid ensures even less rotational variance than normal.
Cheers
[…] deceptive. Higher maybe to make use of the computed free vitality? When that is accomplished, as we noticed within the earlier publish, the transition state for proton switch as situated within the complete vitality floor can even […]