The annual “molecule of the year” results for 2021 are now available … and the winner is Infinitene.[cite]10.33774/chemrxiv-2021-pcwcc[/cite],[cite]10.1021/jacs.1c10807[/cite] This is a benzocirculene in the form of a figure eight loop (the infinity symbol), a shape which is also called a lemniscate [cite]10.1021/jo801022b[/cite] after the mathematical (2D) function due to Bernoulli. The most common class of molecule which exhibits this (well known) motif are hexaphyrins (hexaporphyrins; porphyrin is a tetraphyrin)[cite]10.1039/b502327k[/cite],[cite]10.1021/ol0521937[/cite],[cite]10.1002/chem.200600158[/cite], many of which exhibit lemniscular topology as determined from a crystal structure. Straightforward annulenes have also been noted to display this[cite]10.1107/S1600536811048604[/cite] (as first suggested here for a [14]annulene[cite]10.1021/ol0518333[/cite]) and other molecules show higher-order Möbius forms such as trefoil knots.[cite]10.1038/NCHEM.1955[/cite],[cite]10.1039/D0CC04190D[/cite] This new example uses twelve benzo groups instead of six porphyrin units to construct the lemniscate. So the motif is not new, but this is the first time it has been constructed purely from benzene rings.
The molecule has D2 chiral symmetry and is shown below (click on the image for the 3D model obtained from the crystal structure).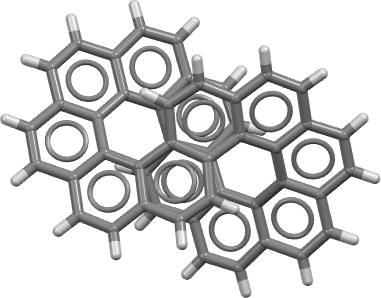
The authors suggest that the aromaticity in a D2-symmetric [12]-circulene is confined to six “Clar” rings each of six electrons, and is not delocalised around the entire molecule. For a molecule with this topology (defined by a linking number, Lk = 2π[cite]10.1016/j.comptc.2014.09.028[/cite]) the entire system would be defined as aromatic (delocalised) for 4n+2 electrons and antiaromatic for 4n electrons around a continuous annulene loop. In this example outer annulene circuits of either 34 or 38 carbons can be constructed which retain D2-symmetry and which both follow the 4n+2 rule, whilst a small inner circuit of 14 carbons can be also be constructed. There are probably other D2-symmetric circuits that could be constructed.
When I saw the molecule, I asked myself what the calculated chiroptical properties for the molecule might be; the optical rotation of the two (separated) enantiomers of [12]-circulene were reported as +1130° (P,P) and -1112° (M,M). The calculated value (ωB97XD/Def2-TZVPP) is in excellent agreement. I have also included versions of this system with [11] and [10] benzo rings, which will be discussed in a future post.
| Benzene units | optical rotation (589nm), ° | DOI |
|---|---|---|
| 12 (P,P) | +1143 | 10.14469/hpc/10000 |
| 11 (P,P) | +1025 | 10.14469/hpc/10037 |
| 10 (P,P) | -163‡ | 10.14469/hpc/10001 |
For good measure, the calculated VCD spectrum
Now to the geometry, as obtained from the crystal structure. The [12]circulene shows in total 12 short lengths of 1.348ű0.014, indicating significant localisation in the system. The D2-symmetric C34 path through the system shows a mean length for each bond of 1.405Å, with a maximum value of 1.443Å and a minimum 1.334Å. For this path, the topology of the system indicates Lw = 2π = 0.393Tw + 1.607Wr[cite]10.1021/ja710438j[/cite] This means that most of the coiling of the molecule that results in that figure eight is actually comprised of a topological property known as writhe (Wr) rather than adjacent twisting (Tw) of the p-orbitals. This retains much p(π)-p(π) overlap and hence stabilisation. The values for the inner C14 route are Lw = 2π = 1.256Tw + 0.744Wr which is more highly twisted than the larger outer pathway and so aromaticity via this route is less favoured due to less favourable p(π)-p(π) overlaps.
I also note that the Lw = 2π is an alternative chiral descriptor to the helical notation of (P,P). The (M,M) form would have Lw = -2π. The linking number is more general for more complex helical forms such as trefoils, cinquefoils, hexafoils etc.
So it turns out that this molecule has a fascinating challenge for trying to describe its extended delocalised aromaticity (rather than localised six-membered Clar rings), since more than one “annulene route” for which the “Hückel/Möbius rules” might apply exists.[cite]10.1016/j.comptc.2014.09.028[/cite] Given that the maximum bond length for one of those routes (the [34]annulene) is 1.443Å, there may well be a contribution from this mode of aromaticity other than that from the Clar rings.
I hope to take a look at the [11] and [10]circulenes in a future post.
‡The explanation for this sign inversion is delightful but too complex to give here.[cite]10.1002/chir.22486[/cite]
This post has DOI: 10.14469/hpc/10036
Hello sir,
Thank you for this nice post. I really enjoyed reading it. You might like to take a look at the final version published in JACS (https://pubs.acs.org/doi/10.1021/jacs.1c10807) and perhaps update the links, as for now, there is a reference to the preprint. I also look forward to reading your posts on analogous [11]- and [10]circulene.
Kind regards,
Maciej Krzeszewski
Great to hear from you Maciej! I have added the citation for the final article.
Hello, I’m the editor of ACS’s Molecule of the Week. We intend to feature infinitene in our May 30 edition. I have read the available papers on this molecule, and I have one question that I hope you or Maciej Krzeszewski can answer:
How are the designations (M,M)- and (P,P)- defined? I thought I knew a lot about chemistry nomenclature, but I have never run into these before. Thank you in advance for your reply.
Greetings Michael. The chirality is a general form known as axial chirality, sometimes also helical chirality and relates to the sense of direction of rotation of the axis or helix. It is explained here: https://en.wikipedia.org/wiki/Axial_chirality. A lemniscate, or figure 8, is considered to have two conjoined helices, and if they both rotate clockwise (from closest to furthest from the observing axis) it is designated P,P (P= positive) or M,M ( M=minus) for anticlockwise. We showed (DOI: https://doi.org/10.1021/ja710438j) that a more general computable notation which can be used to achieve the same effect is the linking number, Lk, which can have positive or negative integer values and the value of the integer specifies the number of crossing points in the helical topology.
Michael,
You might also be interested in some history for the idea of a molecule of the (day, week, month, year). Arguably, it started in the early days of the WWW with the publication in 1994 of this communication DOI: https://doi.org/10.1039/C39940001907 and the follow up full article DOI: https://doi.org/10.1039/P29950000007 Wondering how to exploit some of the features described there, three chemistry departments in the UK decided to launch a molecule-of-the-month feature in late 1995. The history of the project was described some 20 years later at https://doi.org/10.3390/molecules22040549 One of the original URLs is https://www.ch.imperial.ac.uk/motm/ and the one at Bristol continues to add monthly molecules this day @ http://www.chm.bris.ac.uk/motm/motm.htm