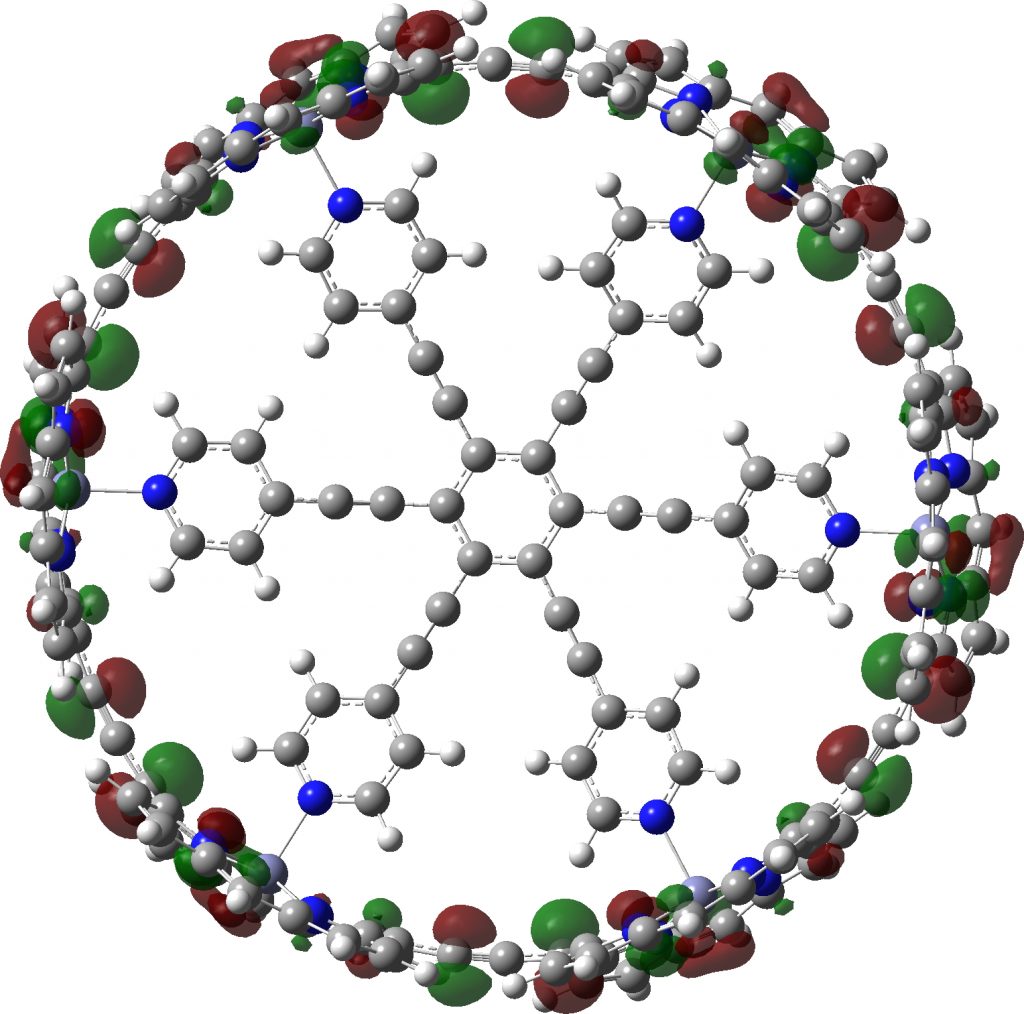
Here is another of the “large” molecules in the c&e news shortlist for molecule-of-the-year, 2020. This one is testing the Hückel 4n+2 rule out to a value never before seen (n = 40, or 162 π-electrons).[cite]10.1038/s41557-019-0398-3[/cite] The take-home message is that this rule seems to behave well in predicting global aromaticity even at this sort of scale!
The smallest and largest of the 34 examples for which coordinates are provided are shown below. The smallest example has “only” 300 atoms, whilst the largest has 1008,‡ which is certainly something for which the wavefunction would be analysed for its NICS aromaticity indices.
c-P6e6_neutral
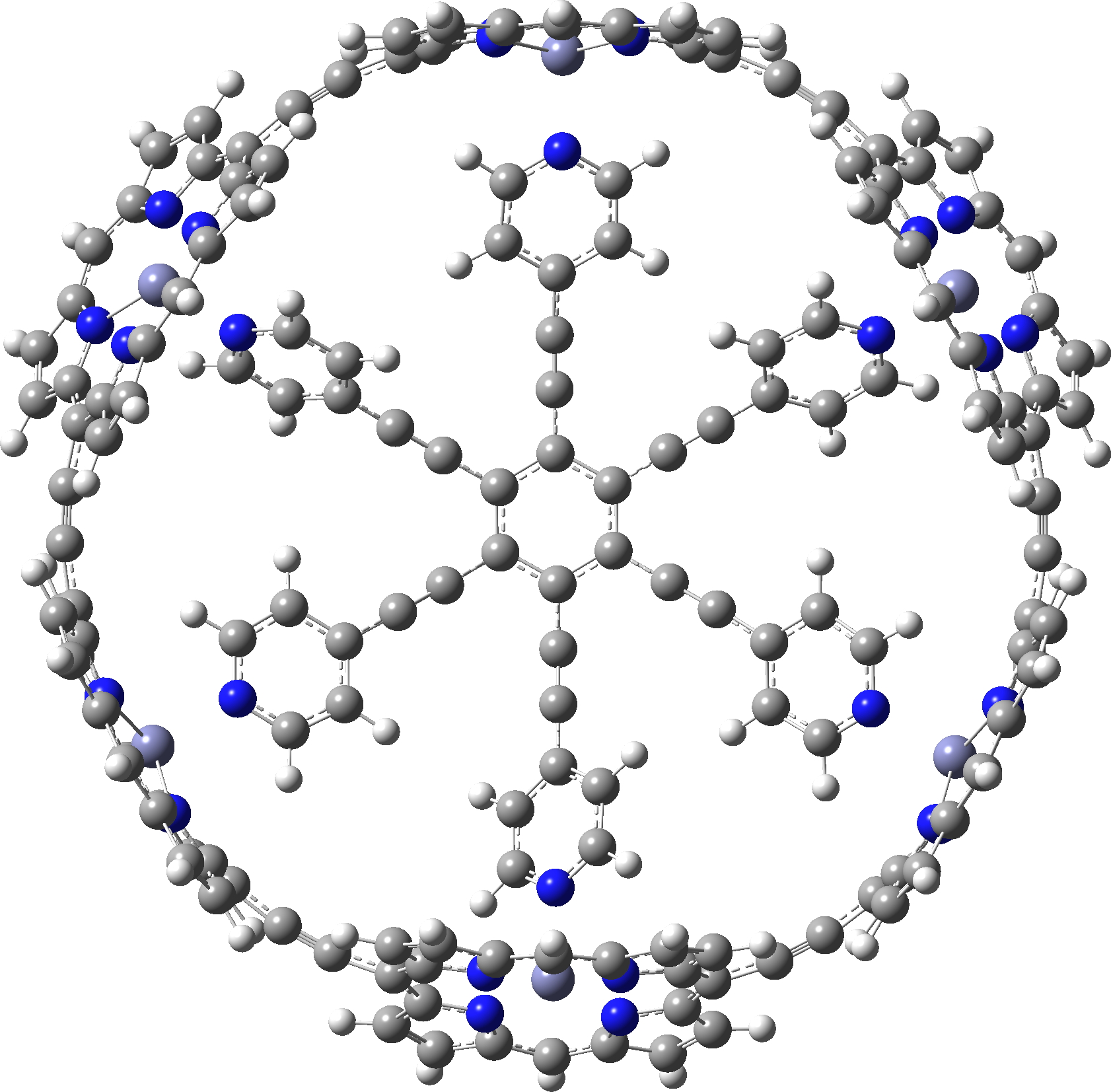
c-P12b12_T6ef
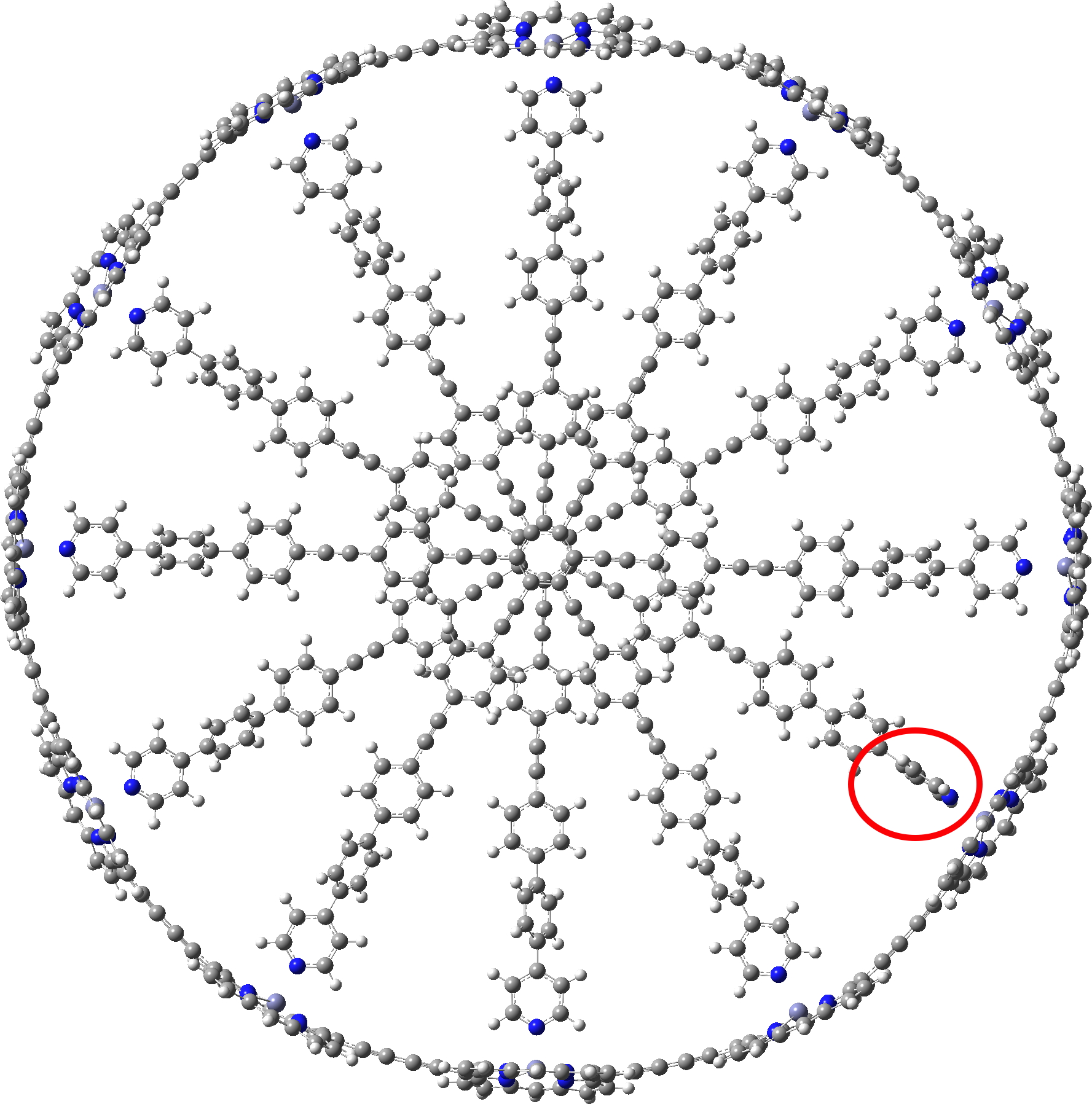
A point of interest is the symmetry of these systems. My attempt to “symmetrise” the provided coordinates did not succeed, probably because the structure provided was insufficiently symmetric to succumb to this.♥ Initially at least it seems the larger “bicycle-wheel” structure might have as much as twelve-fold symmetry, with twelve zinc porphyrin units in the outer ring. But with the coordinates displayed in a rotatable 3D model, I quickly noticed one pyridyl ring acting as a spoke and ringed in red. Its orientation is different from all the others! Is this significant? You decide for yourself by clicking on either of the images above to load the 3D coordinates.
I also include a fascinating Möbius “lemniscular” version, which has a linking number Lk=2 and so also follows the 4n+2 rule.[cite]10.1021/ja710438j[/cite],[cite]10.1021/jo801022b[/cite]
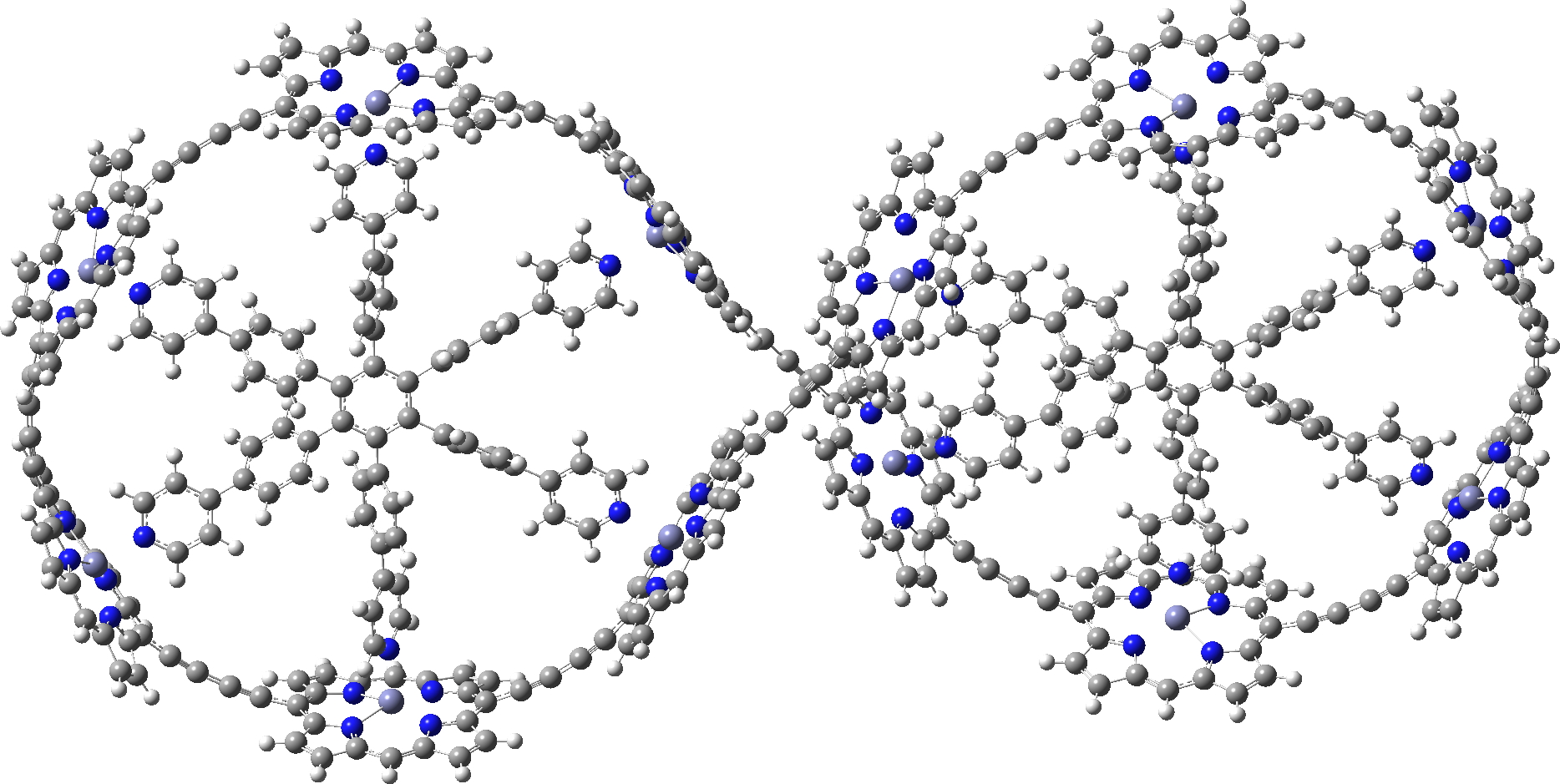
c-P12[b12]_T6f
Postscript A note on symmetrization. If a geometry is approaching symmetry, one can try an automatic algorithm in the molecular display programs to complete the process. But if the symmetry is still some way off, other methods based on energy minimisation must be tried. Molecular Mechanics in this instance is problematic, since all the bond types for the force field to be used must be set, and symmetrically at that. That is a big task. Far better to use a quantum mechanical method, which does not rely on bond types. Given the sizes of the molecules, I here select the PM7 semi-empirical procedure. It can handle in excess of 1000 atoms with no real difficulty and this version of the AM/PM series has the added advantage that it contains a dispersion attraction correction. This might be expected to be important in these types of molecule. Firstly c-P6e6_neutral, for which C6-symmetry can be achieved. A full PM7 optimisation takes ~10 minutes. This reveals that the distance between adjacent ortho-hydrogen atoms on the pyridyl spoke is 2.21Å, which is typical of a dispersion attraction (and a distance for which inclusion of a dispersion term is vital). The original coordinates have values ranging from 2.7 – 3.4Å.
c-P6e6_neutral with six-fold symmetry
The symmetrisation of c-P12b12_T6ef to C6 is also possible using prior PM7 optimisation, with non-bonded H…H contacts now all as pairs of 2.504 and 2.352Å each originating from a different central dendrimer unit. The original coordinates had H…H contacts as short as 1.6Å, which is very unreasonable.
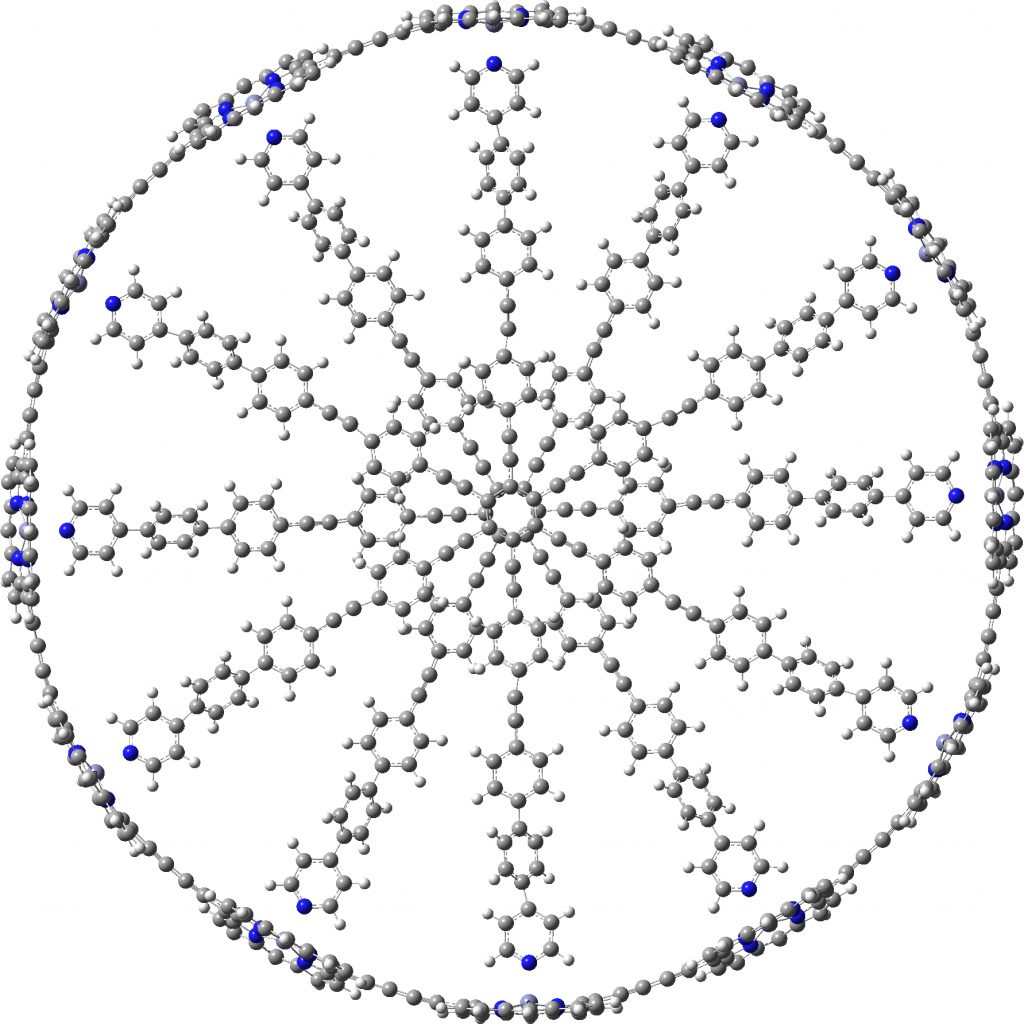
C6-symmetric c-P12b12_T6ef
‡A common format for expressing coordinates is the so-called MDL Molfile. This has one advantage over the much more simple XYZ file as provided in the supplementary information of the article in that it defines atom and bond types. This in turn sets the coordinates up for a molecular mechanics optimisation of the geometry. But the molfile, which originated decades ago, does not work for molecules with 1000 atoms or more! Why? Because at the top of the file are two indices, the number of atoms and the number of connected bonds. For this molecule, these strings look like 10081128. In other words because each can carry only three integers, they flow together without an intervening space and end up confusing programs. I used the Sybyl Mol2 format for these coordinates, which does not have this issue. ♥The non-bonded closed H…H contacts are now shown as labels on the 3D model, and you can see for yourself the asymmetry.