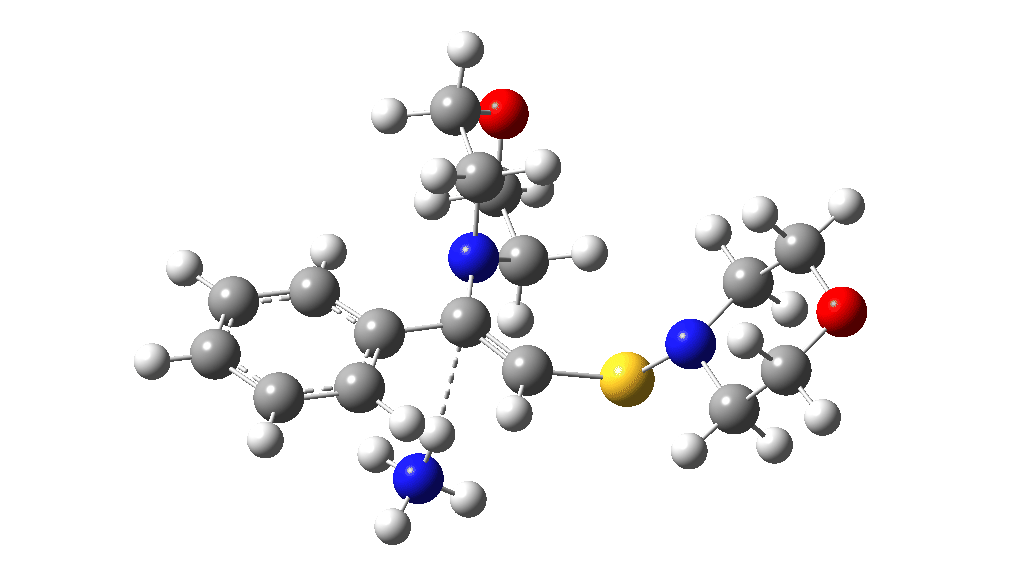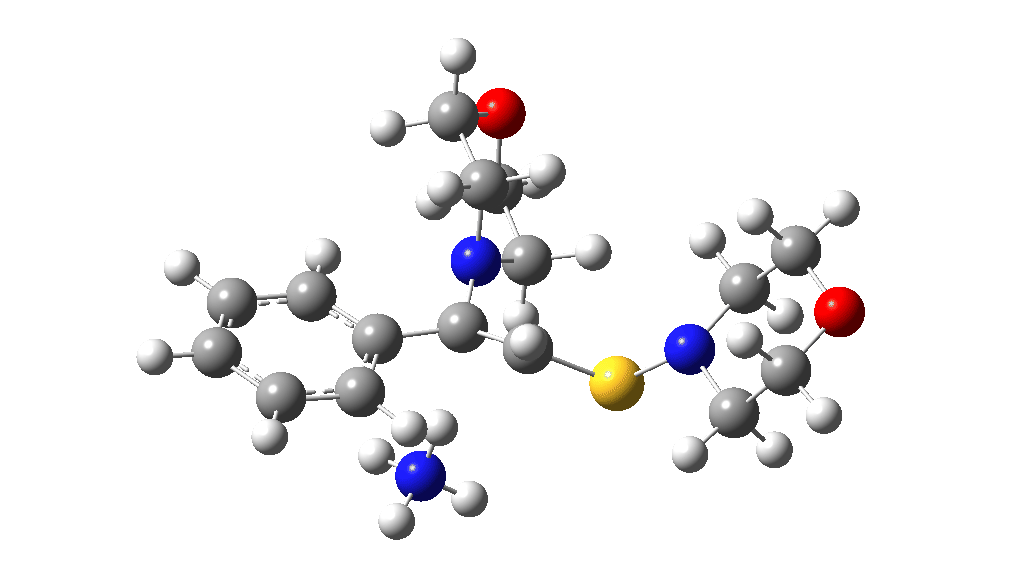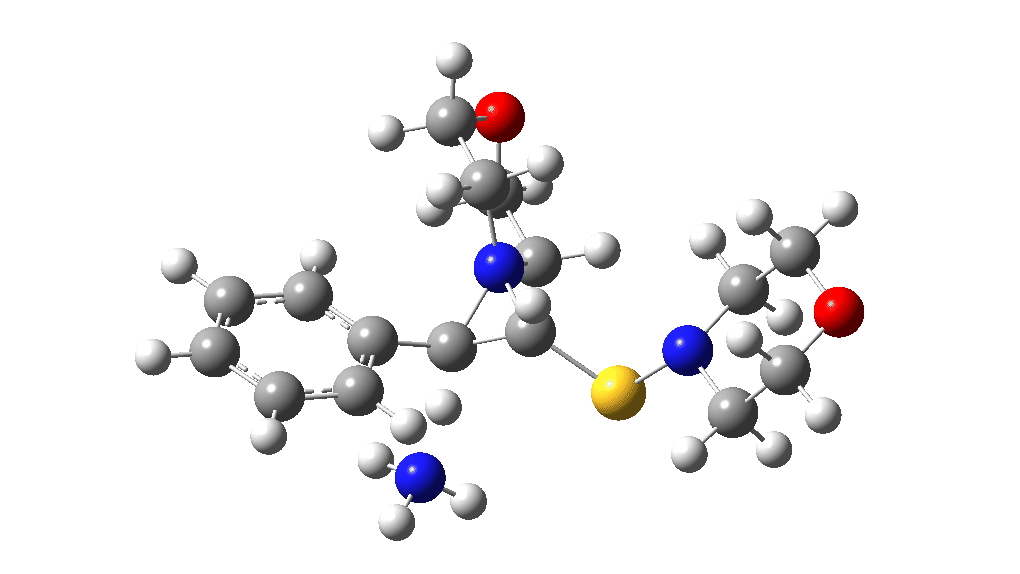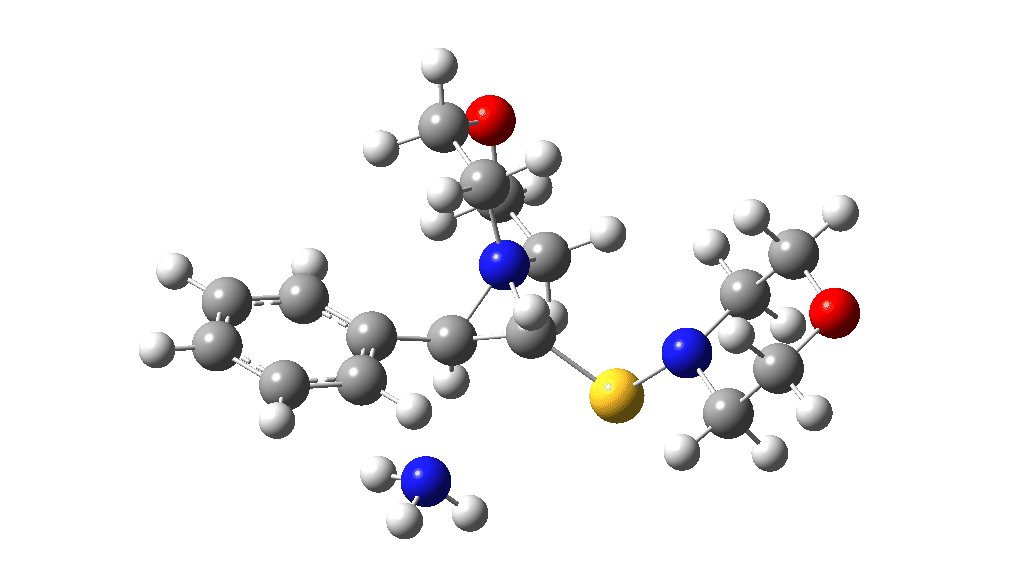
The two previous surveys of the potential energy surface for this, it has to be said, rather obscure reaction led to energy barriers that were rather to high to be entirely convincing. So here is a third possibility.
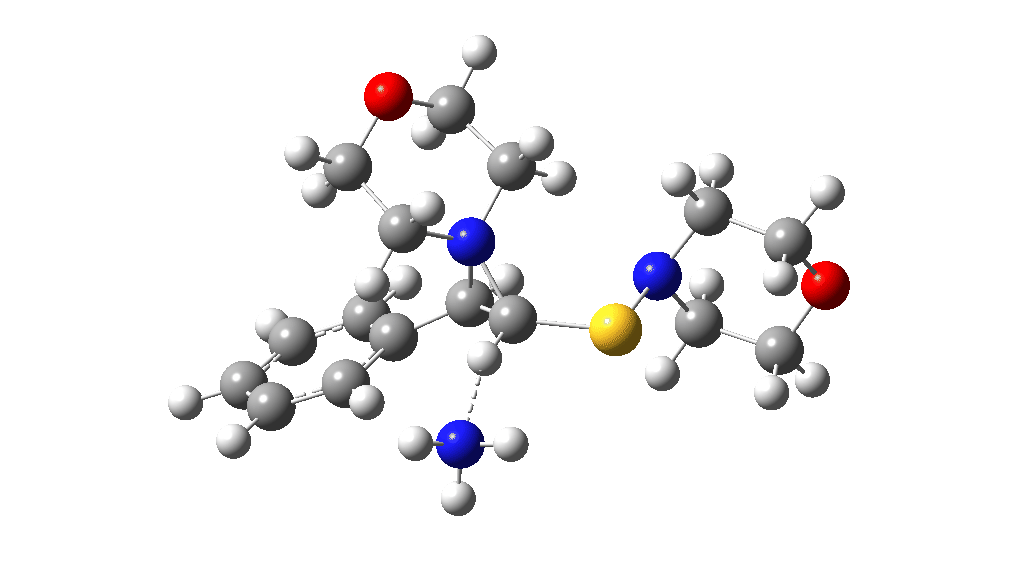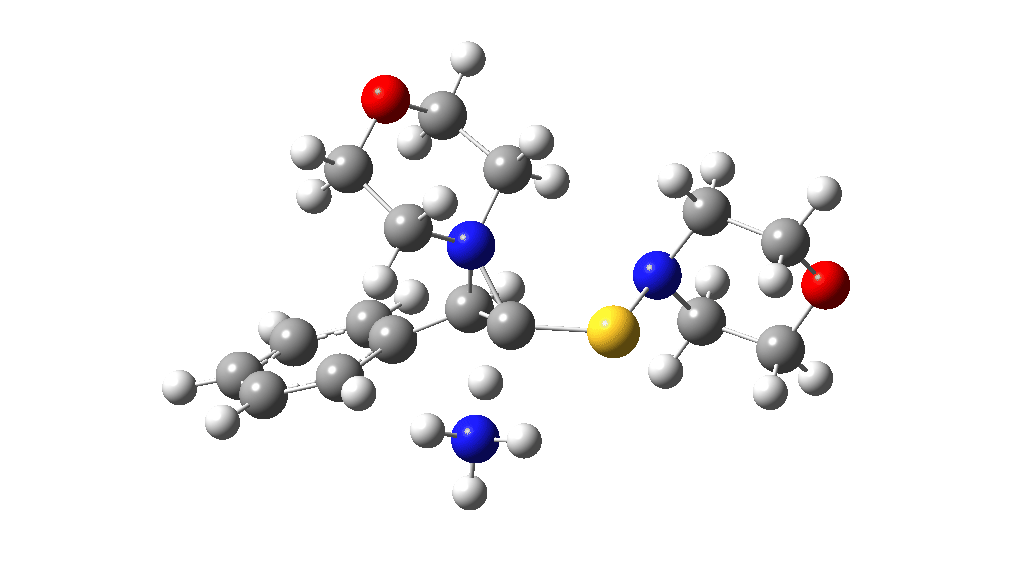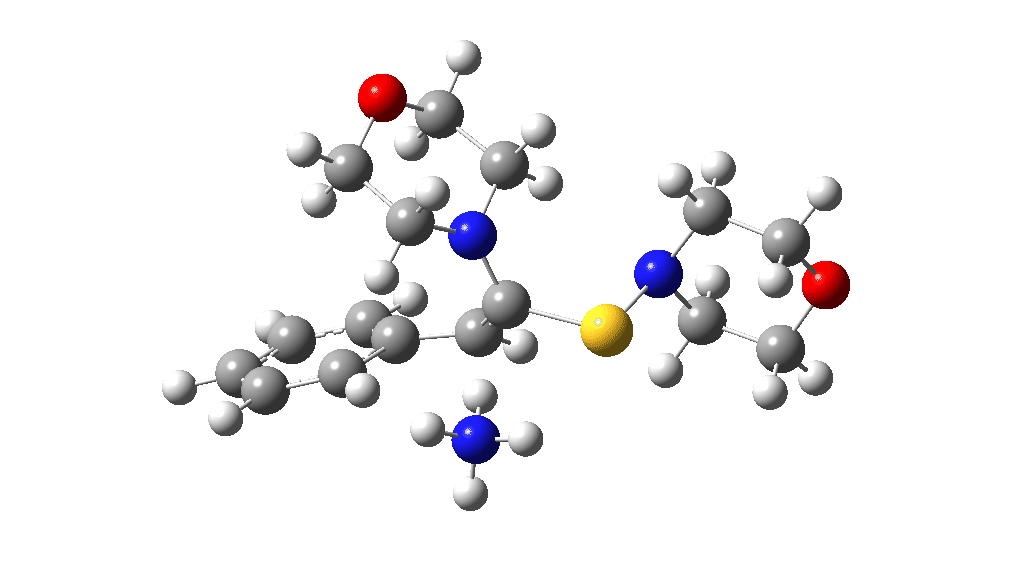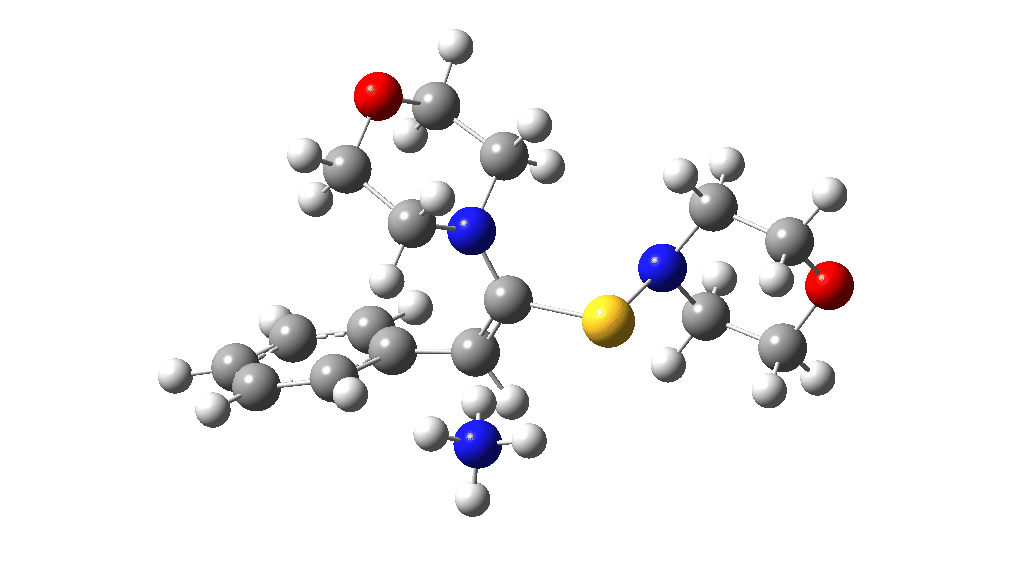
The red section corresponds to the previous exploration, in which a 3-membered sulfur ring intermediate was mooted. Here we go back to a 3-ring with nitrogen instead. The key aspect is the formation of this aziridinium cation species labelled Int4. This mechanistic step can be considered in two ways:
- As a concerted E2-type addition/elimination reaction, with the leaving group in the elimination step being a quaternary ammonium salt as in the Hofmann elimination. This has a major issue in this case, in that for E2 reactions the two reacting bonds have to be antiperiplanar to each other. If they are part of a 3-membered ring, this alignment is difficult to achieve. This does hint that the mechanism may be either stepwise, or certainly asynchronous to avoid this problem.
- As the stepwise formation formation of a cyclopropyl carbanion via an electrocyclic ring closure of Int1, followed by protonation of the anionic centre to form Int4. These two steps could be stepwise consecutive, or concerted in either synchronous or asynchronous fashion. This then to be followed by the same sequence in reverse, i.e. deprotonation of the aziridine followed by electrocyclic ring opening to form the isomeric Int6. The electrocyclic reaction of cyclopropyl carbanion[1] is a 4n-electron reaction, for which the Woodward-Hoffmann rules stipulate conrotation.
Since locating TS5 and TS6 proved non-trivial, I thought it might be informative to give a blow by blow account of the procedure I adopted.
- The crux of finding a transition state is to identify suitable (internal) coordinates to act as the reaction coordinate. In this example if take the second mechanistic type above, we have a C-N bond length as one (internal) coordinate, we have the C-H and H-N lengths as two more, and finally the most tricky, which is how to define conrotation of the two termini of the forming/breaking C-N bond. This can be done with two dihedral angle definitions at each end of this bond, which gives a total of seven internals that could be components of a reaction coordinate. This is amongst the most complex of reaction coordinate definitions, since most transition states can be approximated by just 1-3 internals.
- I started by specifying the most simple molecule imaginable for this reaction, the cyclopropyl carbanion and its opening to a allylic anion. We are going to ignore any proton transfers at this stage, which reduces the internal reaction coordinates to five. The C-C bond is assumed to have a transition state value of 2.1Å and the two pairs of dihedral angles 45 and 135° to define conrotation. These five coordinates are constrained to these values and all the other (internal) coordinates are optimised. The constrained five are then released and the structure is reoptimised, but specifying that the full force constant (2nd derivative) matrix is recomputed from scratch at each step. This allows the optimisation to operate with the most accurate estimate of the curvatures of the potential energy surface at each step (calcall as a value for the OPT key word in eg the Gaussian program system). This super-strong procedure is computationally cheap for this small molecule, and converges in ~5-6 cycles. The method chosen to perform these calculations was B3LYP+GD3BJ/Def2-SVP/SCRF=water with a superfinegrid integral quadrature, and integral accuracy of 10**-14.
- I note that the reference I cited for this reaction[1] was not helpful, since no transition state geometrical parameters are reported in the article; not even the value of the key C-C bond length at the transition state. This sort of reporting would be considered as quite inadequate by today’s standards.†
- Next, the CH2 in cyclopropyl is replaced by the isoelectronic NH2+ and another C-H is replaced by the substituent S-NH2. The original five reaction coordinate values (the now C-N length and the four dihedral) are constrained to the previously optimised values for cyclopropyl carbanion, whilst again all the rest are fully optimised (modredundant keyword in Gaussian). When that procedure is complete, all coordinates are now fully optimised, this time requiring only an initial calcfc for the 2nd derivatives in the opt keyword. As it happens, the perturbation of the original cyclopropyl carbanion transition state geometry by these new substituents is relatively small, so again convergence is rapid.
- The C-S-NH2 group however has introduced four conformational alternative, including the orientatoin of the nitrogen lone pair. All four are located, and the lowest free energy now selected as the model.
- Next, one C-H is replaced by C-Ph. Again initially the five reaction coordinates are fixed at the previously optimised values, the rest optimised, and then that geometry taken forward for the final step in which all coordinates are optimized.
- The last step repeats step 6, but this time the NH2 groups are replaced by the full morpholine ring system in a chair conformation.
- The final step is to add NH4+ as in B=NH3, oriented so as to hydrogen bond to the carbanionic centre, with an initial C…HN length of 1.9Å. Again this is done by first freezing the five reaction coordinates and the C…HN length whilst re-optimizing the rest and then releasing, as in steps 6 and 7. This then add the proton transfer into the model. Finally, the transition states are recomputed with a better (Def2-TZVPP) basis set.
This procedure finally leads to TS5 and TS6.‡ The IRC (intrinsic reaction coordinate paths) for each are shown as animations below, which clearly show that whilst the electrocyclic ring opening is a distinctly different phase from the proton transfer, these two basic steps are nonetheless part of the same concerted (albeit asynchronous) process. In other words, there is only one transition state connecting eg Int1 and Int4 and no discrete, only hidden, intermediates HI1 or HI2. These are revealed by the inflexions in the energy profiles at ~IRC = -1 (TS5) and ~ -1.5 (TS6) rather than the minima you would see for a true reaction intermediate.
Well, after all that effort, the high points in the potential energy surfaces relative to the reactant are again >60 kcal/mol, too high to be realistic. But one has certainly learnt a lot about how to chart potential energy surfaces. Whilst much of the time this turns out to be a relatively simple process to explore, in this particular case it is proving especially tricky to find a pathway of reasonable (~30 kcal/mol) energy.
‡The data are at DOI: 10.14469/hpc/7356. †To be fair, when this was done in 1971, we are in the very dawn of transition state location for complex molecules (i.e. those with more than a few atoms) and many of the techniques used were still evolving rapidly, including how data was being reported and how the transition state was characterised as having one negative force constant.
References
- M.J.S. Dewar, and S. Kirschner, "MINDO [modified intermediate neglect of differential overlap]/2 study of aromatic ("allowed") electrocyclic reactions of cyclopropyl and cyclobutene", Journal of the American Chemical Society, vol. 93, pp. 4290-4291, 1971. https://doi.org/10.1021/ja00746a033