Some areas of science progressed via very famous predictions that were subsequently verified by experiments. Think of Einstein and gravitational waves or of Dirac and the positron. There are fewer well-known examples in chemistry; perhaps Watson and Crick’s prediction of the structure of DNA, albeit based on the interpretation of an existing experimental result. Here I take a look at a what if, that of John Kirkwood’s prediction of the absolute configuration of a small molecule based entirely on matching up the sign of a measured optical rotation with that predicted by (his) theory.
The confirmation that Emil Fischer’s 1891 proposed convention for the absolute configuration of sugars was in fact correct was famously made by Bijvoet in 1951 using crystallography.[cite]10.1038/168271a0[/cite] I first told this story in 2012, noting that Kirkwood apparently made his seminal contribution a year later in 1952[cite]10.1063/1.1700491[/cite] using his quantum mechanical theory of optical rotation to independently come up with the same result. Nowadays he rarely gets the credit for solving the problem of absolute configuration. But wait, Kirkwood’s first stab at solving this problem in fact came in 1937,[cite]10.1063/1.1750060[/cite] a full 14 years before Bijvoet’s famous result (for which incidentally the Nobel prize was not awarded).
I have been asked to talk about this story at a Historical meeting of the Royal Society of Chemistry in March 2020, and for this purpose thought I should take a closer look at Kirkwood’s 1937 article. In it, he sets out his quantum mechanical theory of optical rotation. Remember that in that era, there was no recourse to computers and solving the required (heavily approximated) equations had to be done entirely using mechanical calculators. Kirkwood chooses to analyse the following molecule;
I have redrawn it below in more modern form (and name). The difference between the two is in the notations d and (R). The former relates to the sign of the measured optical rotation [α]D where d stands for dextrorotation, or clockwise and is also often represented by (+).♥ (R) is the modern notation for the absolute configuration shown by Kirkwood in his diagram (Fig. 1).
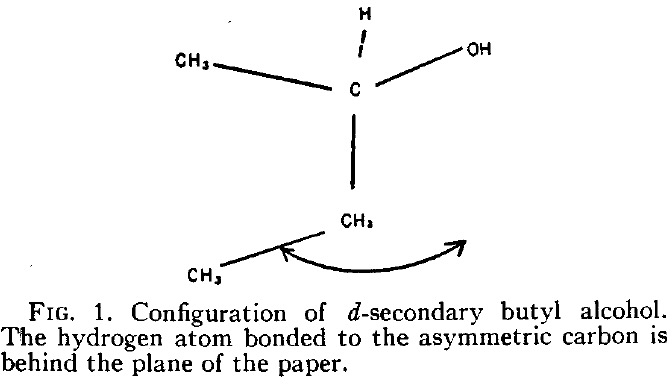
He is asserting below that the enantiomer of butan-2-ol with a measured rotation of 13.9° has (in modern notation) the absolute configuration (R) because his calculations predict somewhere between 9.5° and 21.9° for this specific three-dimensional geometry. So why is Kirkwood not lauded for solving this problem in 1937? Well, because we now know that (R)-butan-2-ol has a negative rotation of -13.9°![cite]10.1021/ja803119p[/cite]
Kirkwood is however very aware of the potential problems with his approach. In a nutshell, conformation! In particular, the conformers resulting from rotation about the central C-C bond and especially the C-O bond, where for the purposes of his theory he assumed axial symmetry about that bond.
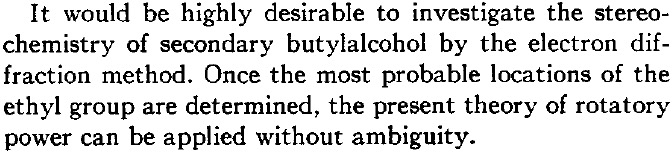
and
Now, in 1937 the area of such conformational analysis was hardly known; only in 1948[cite]10.1039/JR9480000340[/cite] would Barton first put it firmly on the map (and win the Nobel prize for this work). So, in attempting his connection between d and (R), Kirkwood was in a sense far too ahead of his time. It worth asking what modern quantum mechanical theory makes of this problem and does it cast any light on why Kirkwood actually got his assignment wrong (in 1937,[cite]10.1063/1.1750060[/cite] although he WAS correct in 1952[cite]10.1063/1.1700491[/cite]).
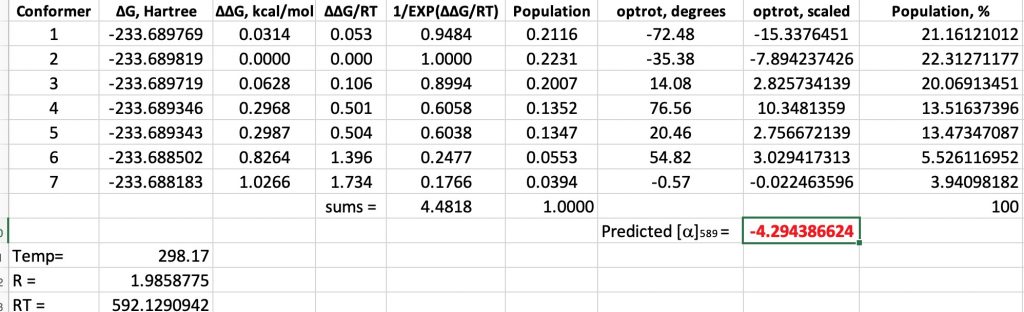
- Firstly, I carried out a comprehensive search of the rotamers about the C-C and C-O bond using molecular mechanics (a method first introduced by Barton in 1948[cite]10.1039/JR9480000340[/cite]) and using the MMFF94 forcefield. This identifies seven distinct conformations arising from rotations about these two bonds. Some warning signs area aready present; these seven are bounded by an energy of only 1.1 kcal/mol! All are likely to have a significant Boltzmann population.
- Next, to ramp up the level of theory to density functional quantum mechanics, at the B3LYP+GD3+BJ/Def2-TZVPP/SCRF=diethyl ether level (FAIR Data: 10.14469/hpc/6367) and at the minimum energy geometry for each conformation, an optical rotation is calculated (at the ωB97XD/Def2-TZVPP/SCRF=diethyl ether) level. Whilst not the highest practical level possible nowadays,† it far exceeds in accuracy what Kirkwood had at his disposal in 1937. The results are at 10.14469/hpc/6367 and available as a spreadsheet if you want to adapt this for your own needs.
What can we conclude?
- All seven conformations have a significant population (at 298K).‡ The ordering, with one small exception, is the same for both Molecular and Quantum mechanics. The relative free energies span a similar range to the steric energies obtained from molecular mechanics (1.0 kcal/mol) and all have a population of >4%.
- Three conformations have a negative or (-) predicted rotation, and four are positive (+).
- When weighted by population, the overall predicted rotation is -4.3°, which compares with that observed (-13°).
- Kirkwood, who was not able to include all seven conformations in his analysis, was deeply unlucky that his particular choices/assumptions of conformations happened to have (+) rotations. But he was very much aware that this result could happen (although he does underestimate this in concluding that his tentative result is “probably accurate”. To be fair, if he had been more realistic, the referees might well have rejected his article!).
So the “what if“.
- If Kirkwood had chosen a conformationally simpler molecule which did not have as many as seven populated conformations, he may well have got his prediction correct (and for mostly the right reasons!).
- But he has to be given lots of credit for recognising that optical rotations can be sensitive to conformational analysis. In this regard he could be regarded as one of the early fathers of that entire (Nobel prizing winning) field.
- He was 14 years ahead of the eventual unambiguous experiment that verified the Fischer convention. Of course he would have needed to correlate the absolute configuration of butan-2-ol with those of both sugars and amino acids using chemical transformations. In 1937, this may well have been quite synthetically challenging (but of course perhaps this correlation may have been actually known at the time. Does anybody reading this know?)
- But given that two other discoveries, both of which won the Nobel prize (the structure of peptides and the structure of DNA), depended on knowing with certainty the absolute configurations of amino acids and sugars respectively, Kirkwood’s method could be argued directly impacted upon no less than three Nobel prizes within two decades of his initial work.
- Remember that Watson and Crick “predicted” that the DNA helix is right-handed, as it happens on the basis of a single “short” H…H contact in their model which apparently disfavoured a left-handed helix. Boy was that a lucky guess (since that conclusion cannot be sustained nowadays on the basis of short H…H contacts). And that Pauling, in his own initial structures suggesting an α-helix in some proteins, predicted (wrongly) that the helix was left handed.
So I think that yes, Kirkwood was pretty unlucky in his 1937 effort. And by 1952 (when he was correct), the opportunity for widespread recognition for this work and perhaps even a Nobel prize, had passed.
♥Stereochemical notation has suffered from some measure of confusion over the years. Much of that confusion was cleared up with the introduction of the CIP rules, but historical vestiges remain. Thus d was originally used by Fischer himself to indicate configuration using the sense of direction on his diagram, but by others (including Kirkwood in 1937) to indicate the sense of direction of polarised light, an entirely different property. Eventually, the configurational sense became distinguished from the rotational light sense by capitalising the former (which of itself can still lead to confusions). Nowadays, the configuration of an entire molecule tends to be described by specifying the absolute configuration of all the asymmetric units using the CIP formalism, whilst Fischer’s formalism (now rationalised D/L), is only applied to sugars and cannot be used generally for other molecules. ‡If you want to explore the temperature dependence of the Boltzmann populations and hence the predicted change in rotation with temperature, do please download the spreadsheet and try it out for yourself! †The elapsed time for these 14 calculations took about 2 hours. The exhaustive molecular mechanics calculations took <20 seconds.
For completeness, I here report calculations done according to the procedures reported above for the two compounds Kirkwood reported in his 1952 article.
1. 2,3-epoxybutane (modern name (2R,3R)-2,3-dimethyloxirane). This has no conformational ambiguity. The measured value is [α]D = 59°. Kirkwood et al report a calculated value of 43°. Using B3LYP+GD3+BJ/Def2-TZVPP/SCRF=heptane, one gets 58.4°. These all match.
2. (R)-1,2-dichloropropane (see Fig 2, from ref 2 above), which is prepared by chemical transformations from the first molecule, with an assumed inversion of configuration at the asymmetric centre. This is described as the enantiomorph of the molecule to which the calculations apply. This has three conformations, all populated, and overall the calculated rotation is +14°. (S)-1,2-dichloropropane has a reported measured rotation of -20.8° In table V (ref 2) is reported a calculated value by Kirkwood for this enantiomer of -16° at 298K.
When making these comparisons of configurations, one greatly appreciates the revolution that Cahn-Ingold-Prelog (CIP) in 1966 brought to systematic nomenclature of the asymmetric centres (and which Kirkwood did not have at his disposal).
I do not want to be stalking here, but I have a note to this topic as well:
When I read some time ago about the life of Swiss physical chemist Werner Kuhn (1899–1963; https://en.wikipedia.org/wiki/Werner_Kuhn) I found mentioned that he had “solved” the problem of determining the absolute configuration (of lactic acid, specifically) already in 1936 (10.1515/zpch-1936-3105) based on a quantum mechanical theory of optical rotation he had developed previously (10.1007/BF01516221).
I am really no expert on this, so I wonder why he is usually not mentioned. Was the theory not convincing enough or even invalid from a later perspective? The work seems to have been forgotten somewhat, but was widely cited at the time.
Kuhn also managed to enrich racemic mixtures of α-azidopropionic aicd N,N-dimethylamide by irradiating it with circularly polarized light (10.1007/BF01506782; W. Kuhn, E. Knopf, Z. physik. Chem. B, 1930, 7, 292 – there seems to be no DOI for this one).
I just checked what Kirkwood (10.1063/1.1750060) wrote on the topic and found:
“Its analog in the oscillator theory is to be found in Kuhn’s specialization of Born’s classical formula. However, anisotropic polarizable groups replace the hypothetical dispersion oscillators, and the coupling parameter is explicitly calculated from the electrostatic interaction of the groups.”
It would seem that the theory used by Kuhn was less fundamental (Kirkwood: “It is here that an adequate theory of rotatory power, free from the defects of the artificial oscillator theory, is to be sought.”), but could have been essentially correct in therms of the outcome?
In any case, one notes that scientific progress is often incremental and sometimes several people have similar ideas around the same time…
Thanks Lukas; with insight and knowledge such as yours, I positively welcome your comments!
Re so I wonder why he is usually not mentioned.
Like a long river, which has many tributaries, defining the source is often a subjective judgement. Thus what I have inferred is that whilst Kirkwood’s theory of optical rotation may be closer to the modern approach than Kuhn’s, he too could be considered merely a tributary rather than the actual source. Thus he came to realise (probably in 1937) that he lacked another essential tool to provide a definitive solution, that of conformational analysis and how to obtain the Boltzmann populations. On a “simpler” level, Kirkwood does not note in his 1952 article the absolute necessity for a naming convention for asymmetric centres. In that article, the configurations are merely noted by reference to the direction the molecule rotates polarized light. He resorts to referring to “enantiomorphs” as nomenclature. And in several places it is actually quite unclear what he is referring to (I had to make informed guesses in my footnote). So Kirkwood’s approach could be considered as a tributary, as was Kuhn’s, even if they obtained “correct” or incorrect solutions, to the main river. As I also noted, Watson and Crick did only slightly better than guess the right-handedness of the DNA helix, but I think we all believe that was only a minor imperfection in their theory.
In a sense, perhaps it is our obsession with Nobel prizes, for which there can only be three winners on any topic, that is the issue.
I noted that for (R)-butan-2-ol, Kirkwood calculated a positive optical rotation of between 9.5-21.9°. The measured value is now known to be negative. But if you read the 1952 article the following footnote appears, in which Kirkwood corrects the signs of no less than seven equations.
I am left speculating whether this correction, clearly spotted some time after 1937, were to be applied, would the optical rotation of (R)-butan-2-ol emerge as negative rather than positive? In any case, the complex Boltzmann populations would suggest that any answer obtained for this molecule would be fortuitous.
Lukas mentions that Kuhn determined the absolute configuration of lactic acid. The L-(+)-(S) isomer has a reported rotation of only +4° in water (DOI: 10.1246/cl.2002.758). There are five conformations within 1 kcal/mol of each other, not including hydrogen bonding from the water solvent. So quite a challenging system for Kuhn to select!
I include a paragraph from Kuhn’s 1936 article, showing the notation d(-). In modern terms, that is D-(-)-(R) and in agreement with being the enantiomer of L-(+)-(S), but with a negative rotation. So Kuhn turns out to be correct, but possibly for tenuous reasons.
I noted in my post the association with the absolute configuration of e.g. sugars and amino acids as being essential to attributing the correct diastereomeric relationship of these building blocks to the higher order helical structures of proteins and DNA. I have now been introduced to the work Bart Kahr, who has shown an association between absolute configuration and the helical winds often found in microcrystals of many common organic molecules. See the following articles:
1. 10.1002/ijch.201600002, title: Seeing Molecular Configuration in Twisted Crystal Form.
2. 10.1039/c7ce02107k, title: L-Malic acid crystallization: polymorphism, semispherulites, twisting, and polarity (in the abstract: from the melt, L-Malic acid produces spherulites with helicoidal twisting of its individual fibrils).
3. 10.1021/acs.cgd.9b00910, title: Polymorphism and Morphology Folklore (Molecular crystals with helicoidal morphologies are as common as those that are polymorphic.).
Bart has confirmed to me by email that “enantiomers twist in opposite directions”, that “D and L malic acid have opposite mesoscale twists” and that “when there is an equal probability of right and left crystals, we see both twists”.
Thus, were DNA to be constructed from the enantiomeric ribose, then the duplex helix would wind left-handedly for most sequences (although natural left-handed DNA is observed for some DNA sequences, it being called the Z-form). Equally, only ~0.4% of α-helices in proteins are left handed (10.1016/j.jmb.2005.01.037. These of course are both macroscale structures, rather than the smaller mesoscale ones that Bart has noted.
Finally there is this fascinating article, with amazing photos; 10.1038/s41586-019-1308-y, title: Helical van der Waals crystals with discretized Eshelby twist. In this case, the molecular units have no chirality of their own.