In the previous posts, I tried to track down the onset of bond length alternation (BLA) as a function of ring size in aromatic cyclocarbons, finding the answer varied dramatically depending on the type of method used to calculate it. So here I change the system to an unusual kind of aromatic ring, the leminiscular or figure-eight annulene series.♥ I explore the Kekulé vibration for such species for which a 4n+2 π electron count means they are cyclically Möbius aromatic.[1]
The advantage of using a lemniscular motif compared to the untwisted annulene is that perturbations due to trans-annular steric interactions between inward facing substituents are minimised. Before introducing the results for this type of molecule, I should also explain why the series CnFn is used rather than CnHn. This is because the C-C-H bending vibration is very similar in energy to the Kekulé C-C stretches, causing them to mix significantly and obscure the results. Substitution with F produces “clean” Kekulé modes. You can see this below:
One consequence of introducing two half-twists into the π-system is that this topology gets partitioned into true twist (Tw) and into a different property known as writhe (Wr),[2] the overall effect of which is to reduce the p-π/p-π overlaps of adjacent carbon atoms from suffering two twists to about half this. This in turn may affect the distortive tendency of the π-electrons to induce BLA in the ring.[3] Let us now see what this change of molecule does to the value (and sign) of the Kekulé vibration. Included are conformations for the larger rings which vary in the total number of trans F-CC-F units in the ring. All the FAIR data for these calculations is at DOI: 10.14469/hpc/6139
Two density functional methods have been used, at opposite ends of the spectrum revealed in the previous posts, together with a reasonable Def2-TZVPP basis set.‡ Each ring size can have different isomers, depending on the total number of transoid motifs present. For smaller rings (n=6, 10), the B3LYP+GD3BJ and ωB97XD functionals give very similar results. By n=18 however, a clear divergence has occurred, with the Kekulé modes being real (+ve force constant) for the former and almost equally imaginary (-ve force constant) for the latter.
| CnFn, n= | Kekulé vibration (cm-1) | |
|---|---|---|
| B3LYP+GD3BJ | ωB97XD | |
| 6 (0 trans) | 1305 | 1293 |
|
|
||
| 10 (2 trans) | 1270 | 1067 |
| 10 (4 trans) | 1279 | 1222 |
|
|
||
| 14 (2 trans) | 1235 | 1012 |
| 14 (4 trans) | 1128 | -513 |
| 14 (6 trans) | 1197 | -592 |
|
|
||
| 18 (2 trans) | 974 | -987 |
| 18 (4 trans) | 914 | -1091 |
| 18 (6 trans) | 933 | -1232 |
|
|
||
| 22 (4 trans) | 888 | -1309 |
| 22 (6 trans) | 757 | -1811 |
|
|
||
| 26 (6 trans) | † | -2140 |
| 26 (8 trans) | 756 | -2229 |
| 26 (10 trans) | -437 | -3296 |
Overall, the B3LYP+GD3BJ series shows a slow and reasonably regular decline in the value of the Kekulé modes. As the ring sizes gets larger, the double bond configurations of the rings start to become unstable, with C=C bond rotations occuring during geometry optimisations. At n=26 using B3LYP, we seen a sudden change from a real Kekulé mode mode for the 8-trans isomer to an imaginary one for the 10-trans isomer. As noted above, this abrupt change occurs much earlier with the ωB97XD functional at n=14, with a discontinuity between a conformation with two transoid motifs and the ones with four and six. I can offer no explanation (yet) for this strange abrupt onset of an imaginary Kekulé mode, except perhaps to speculate that it might be related to the Tw and Wr partitioning noted above, given that Tw and BLA might themselves be related. As with the cyclocarbons, the BLA phenomenon seems to be peculiarly sensitive to the method used to compute it, more so than most other molecular properties.
Something deep and important is clearly happening and the underlying cause does need to be identified. It reminds in one sense also of the discontinuous transition between planar aromatic (bond equal) and non-planar non-aromatic (BLA) isomers of 10-π-Dihetero[8]annulenes[4] Who might have imagined that simple aromatic rings could be so tantalisingly complex!
♥ The first example of this was identified in 2005[5] and is characterised by a topological chiral property known as a linking number or Lk. For lemniscular molecules, Lk = 2π, or in plainer english it contains a double half twist in the π system around the ring. ‡This investigation is a perfect example of the benefits of using a data repository. Many of these species were originally included in an article published in 2009[6] with the calculations being deposited in 2007. So all the starting geometries for the present investigation were quickly obtained from that source. †Bonds rotate to 10-trans isomer.
References
- P.L. Ayers, R.J. Boyd, P. Bultinck, M. Caffarel, R. Carbó-Dorca, M. Causá, J. Cioslowski, J. Contreras-Garcia, D.L. Cooper, P. Coppens, C. Gatti, S. Grabowsky, P. Lazzeretti, P. Macchi, �. Martín Pendás, P.L. Popelier, K. Ruedenberg, H. Rzepa, A. Savin, A. Sax, W.E. Schwarz, S. Shahbazian, B. Silvi, M. Solà, and V. Tsirelson, "Six questions on topology in theoretical chemistry", Computational and Theoretical Chemistry, vol. 1053, pp. 2-16, 2015. https://doi.org/10.1016/j.comptc.2014.09.028
- S.M. Rappaport, and H.S. Rzepa, "Intrinsically Chiral Aromaticity. Rules Incorporating Linking Number, Twist, and Writhe for Higher-Twist Möbius Annulenes", Journal of the American Chemical Society, vol. 130, pp. 7613-7619, 2008. https://doi.org/10.1021/ja710438j
- S. Shaik, A. Shurki, D. Danovich, and P.C. Hiberty, "A Different Story of π-DelocalizationThe Distortivity of π-Electrons and Its Chemical Manifestations", Chemical Reviews, vol. 101, pp. 1501-1540, 2001. https://doi.org/10.1021/cr990363l
- H.S. Rzepa, and N. Sanderson, "Aromaticity on the edge of chaos: An ab initio study of the bimodal balance between aromatic and non-aromatic structures for 10π-dihetero[8]annulenes", Phys. Chem. Chem. Phys., vol. 6, pp. 310-313, 2004. https://doi.org/10.1039/b312724a
- H.S. Rzepa, "A Double-Twist Möbius-Aromatic Conformation of [14]Annulene", Organic Letters, vol. 7, pp. 4637-4639, 2005. https://doi.org/10.1021/ol0518333
- C.S. Wannere, H.S. Rzepa, B.C. Rinderspacher, A. Paul, C.S.M. Allan, H.F. Schaefer, and P.V.R. Schleyer, "The Geometry and Electronic Topology of Higher-Order Charged Möbius Annulenes", The Journal of Physical Chemistry A, vol. 113, pp. 11619-11629, 2009. https://doi.org/10.1021/jp902176a
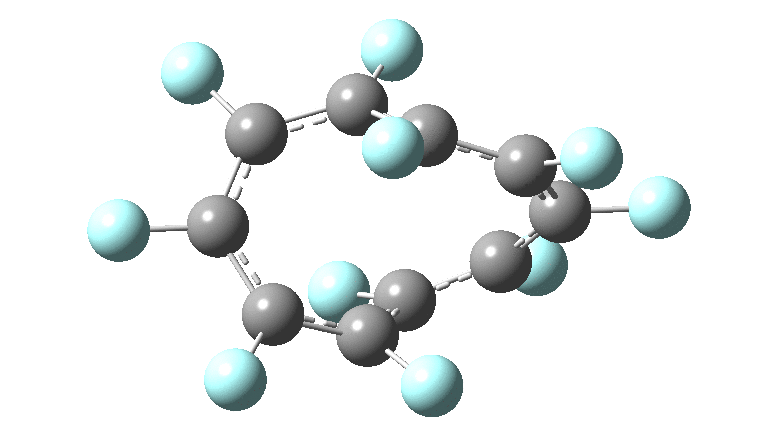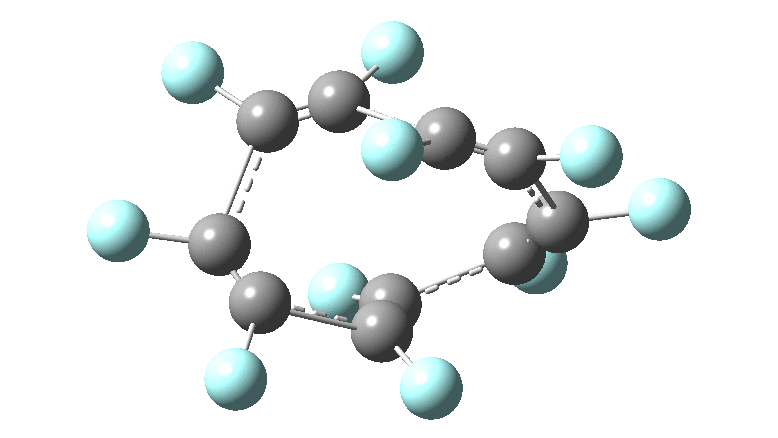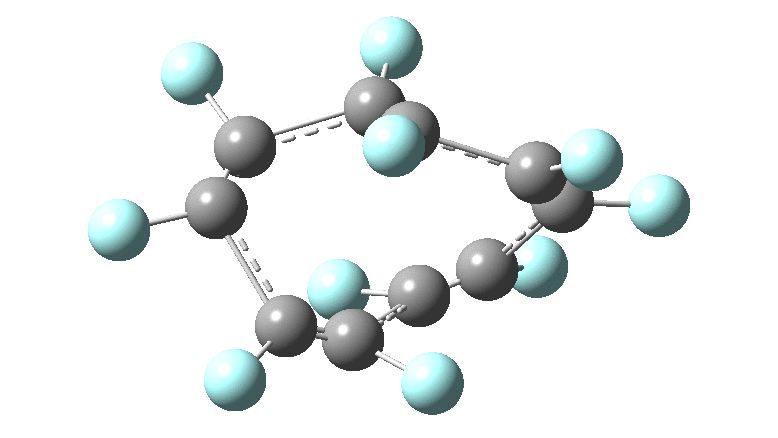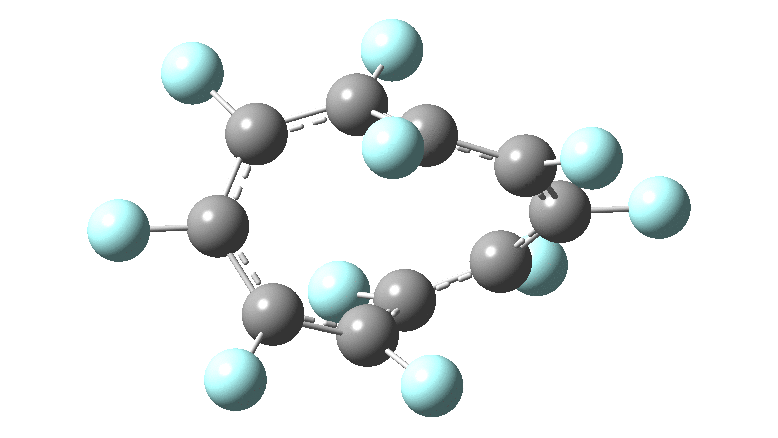
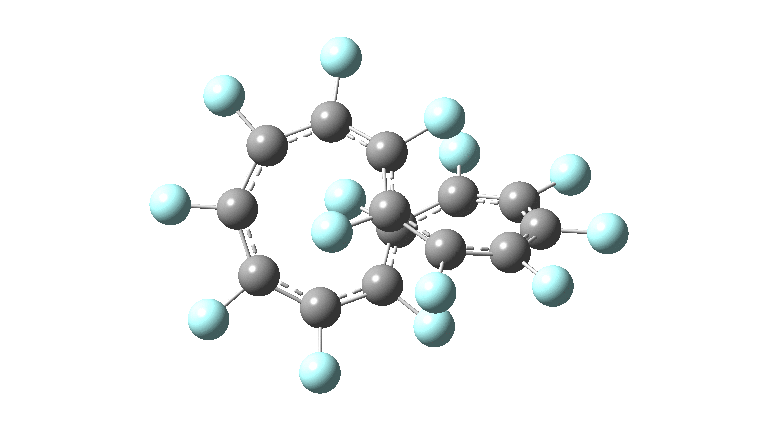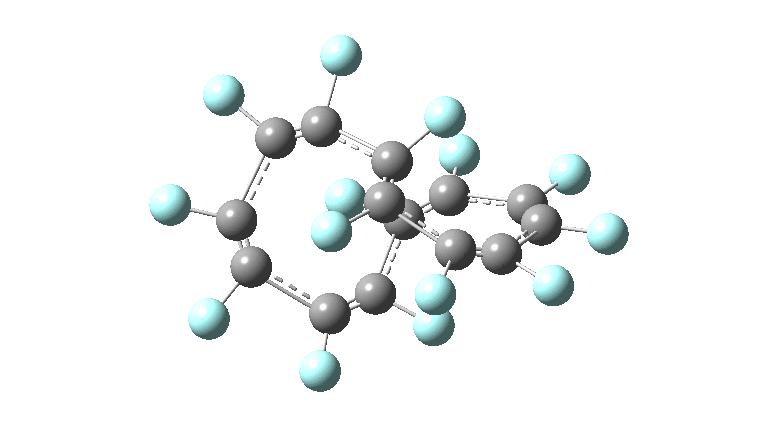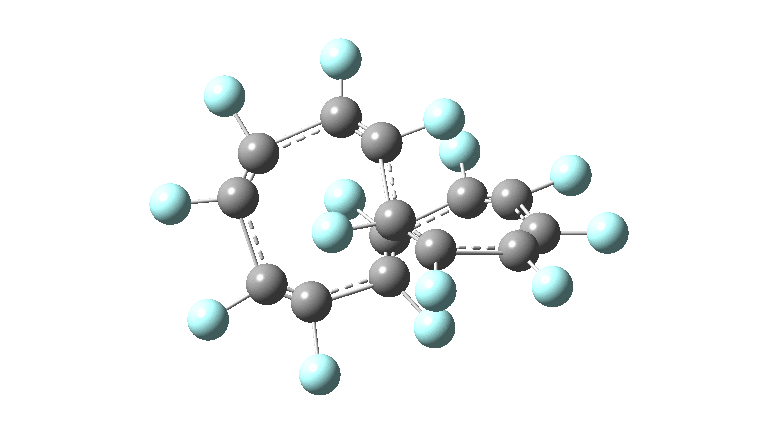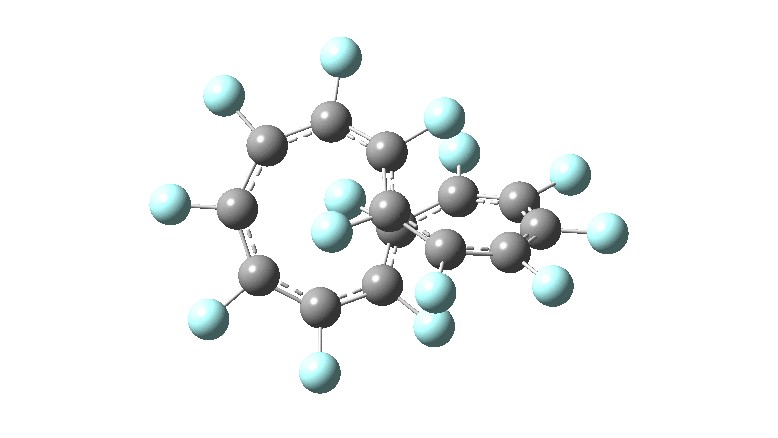
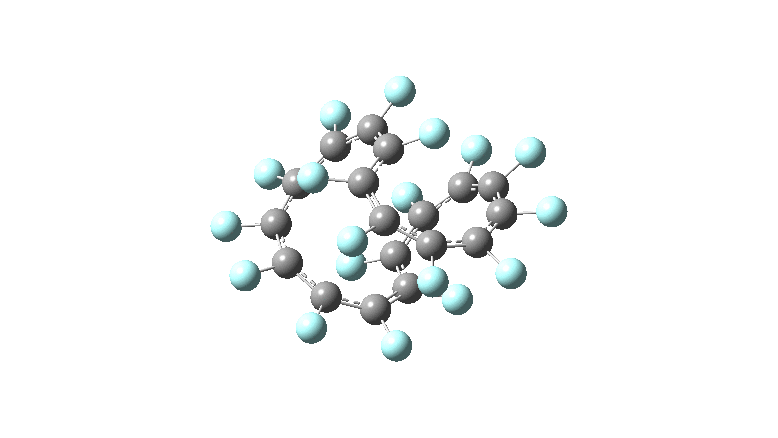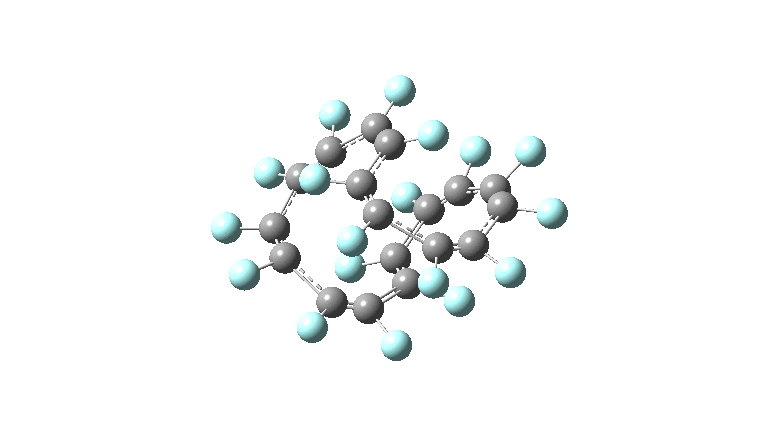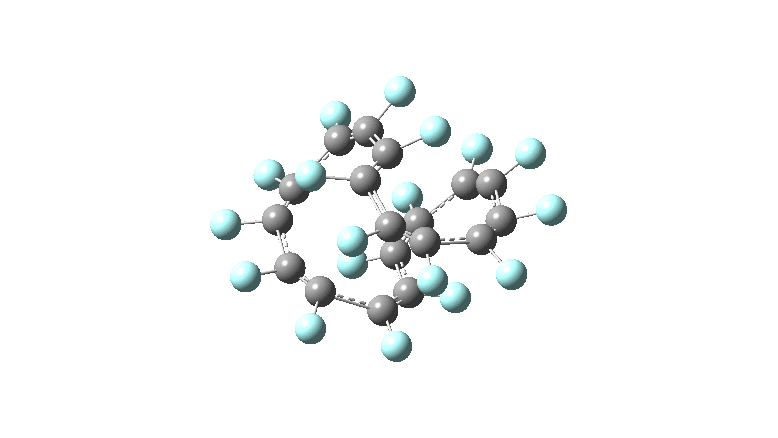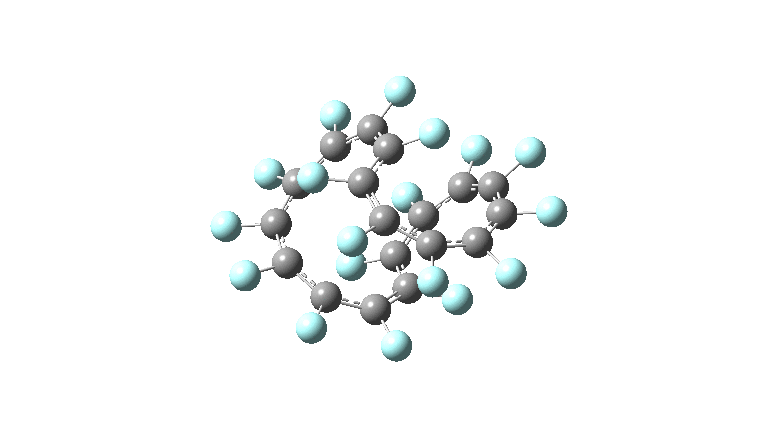
These molecules have much lower symmetry, looking at the animations I would guess probably C2? So one would not expect a pure Kekule mode to exist for these molecules. Watching these vibrations, it seems there is real scope for non-bonded interactions to affect the movements of the atoms, particularly near the crossover points.
All the systems studied in fact have D2 symmetry, as appropriate for a “figure-eight” or lemniscular molecule. I attach the Kekule vibrations for the C26F26 system (B3LYP) showing animations of the +756 and -437 modes noted in the table. Both seem pretty “pure” Kekule modes.
There are, less commonly, some systems however where the mixing with other modes, perhaps at the cross-over points, means that no Kekule mode can be identified.
The log file for all the entries in the table can be downloaded from DOI: 10.14469/hpc/6139 and you can inspect the normal modes, including those I have claimed as being Kekule-like, for yourselves. Both the (free) Avogadro program and the (licensed) Gaussview program support such animations (I am sure there are other programs that also do).