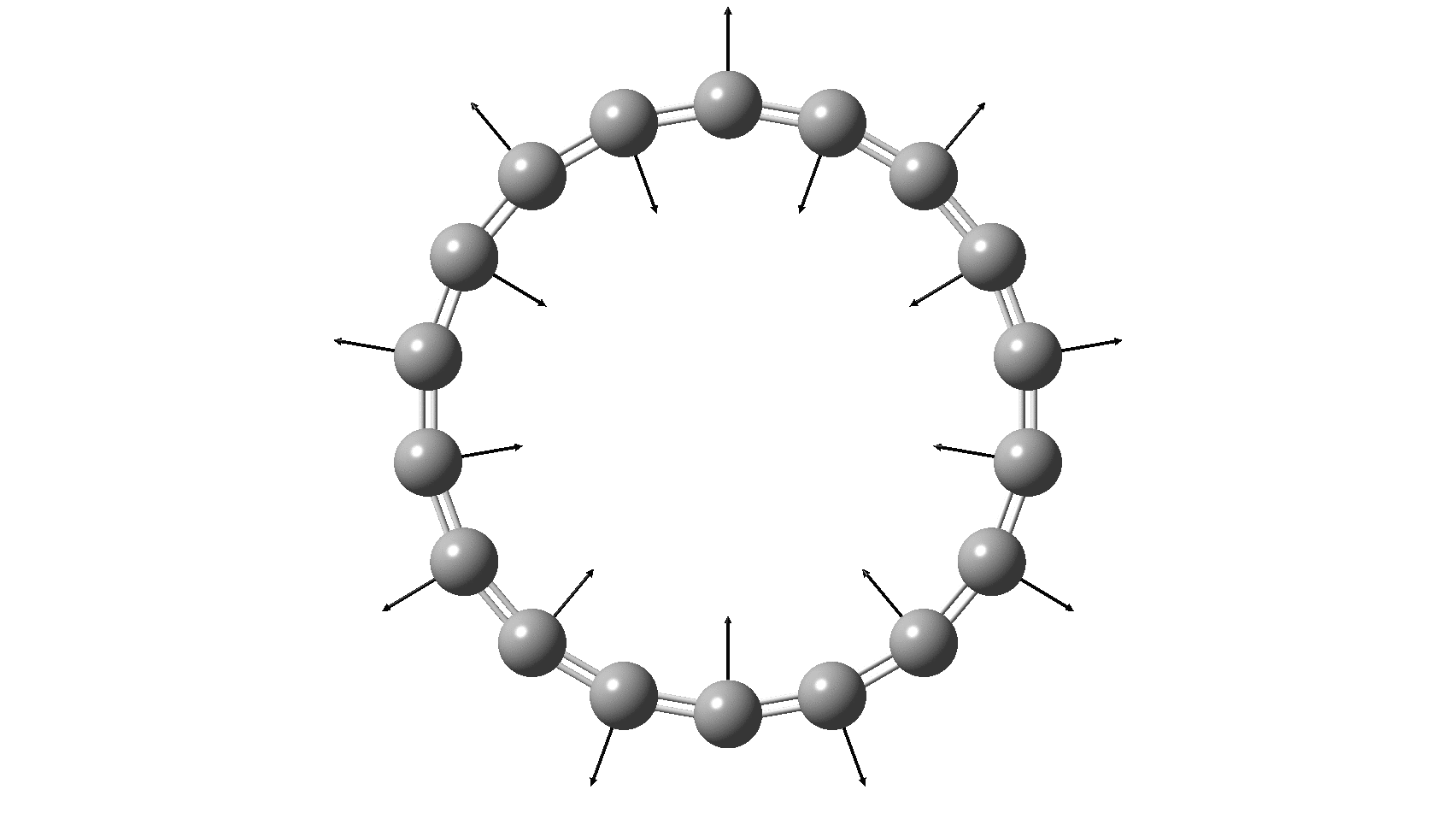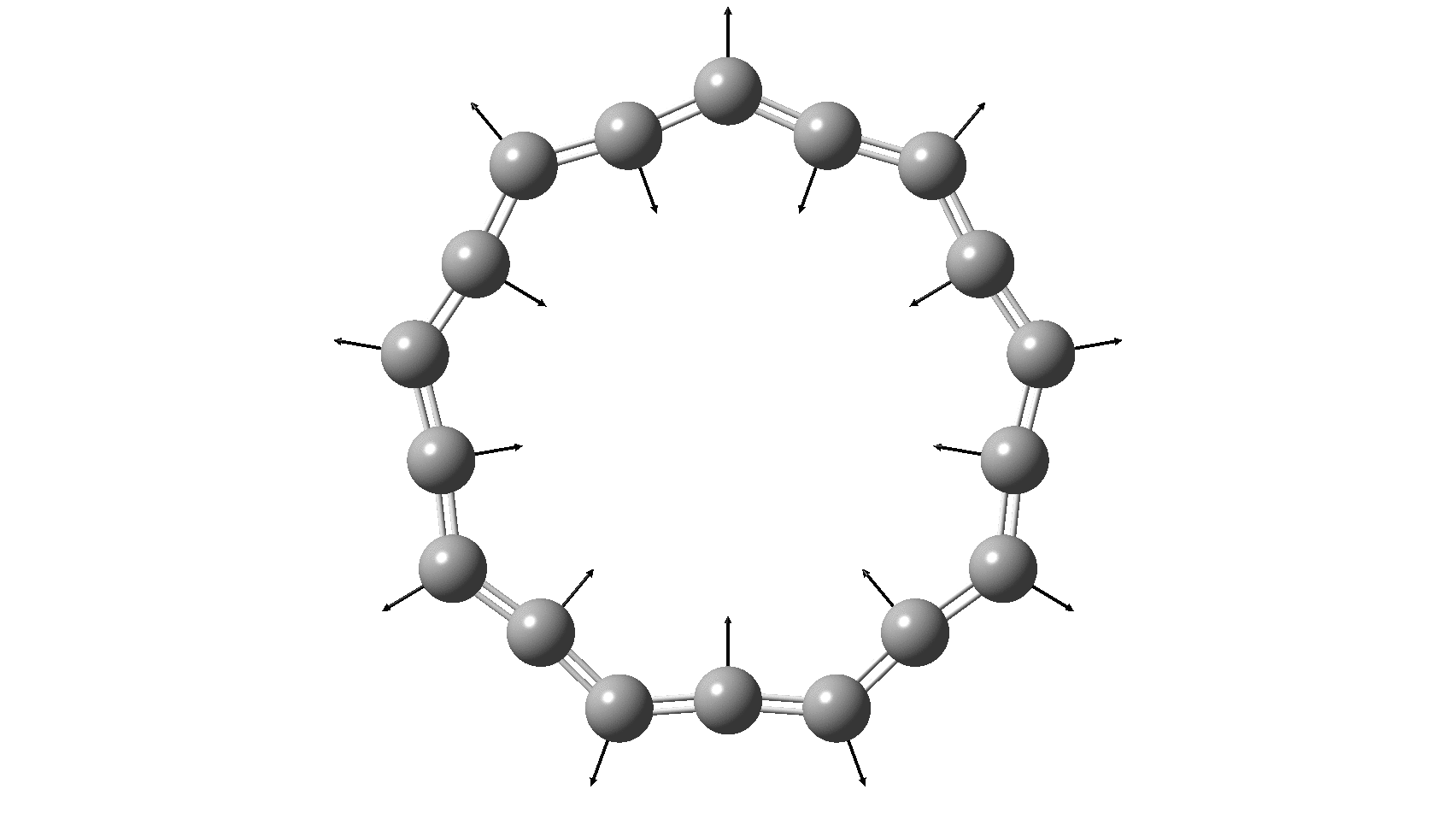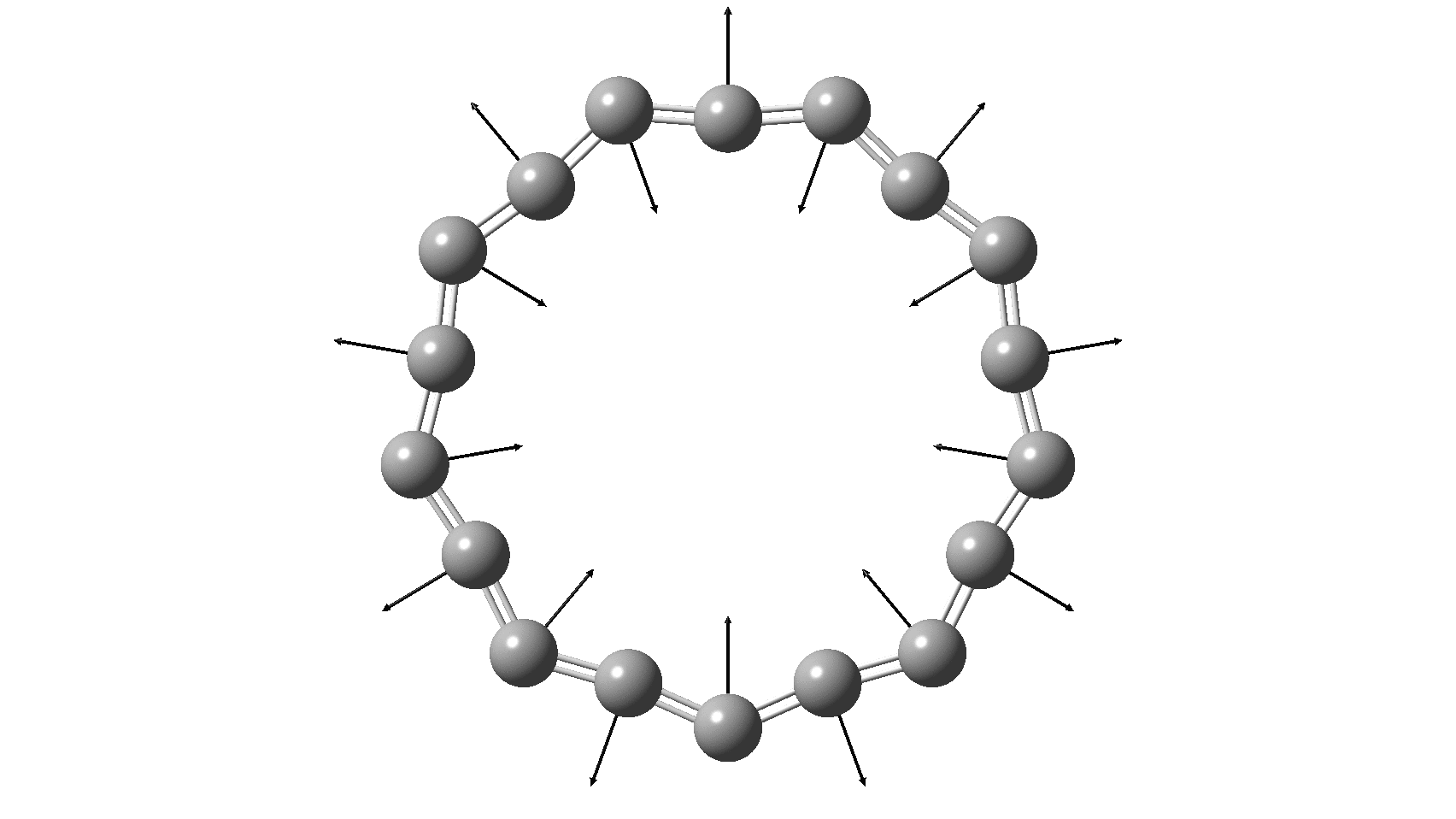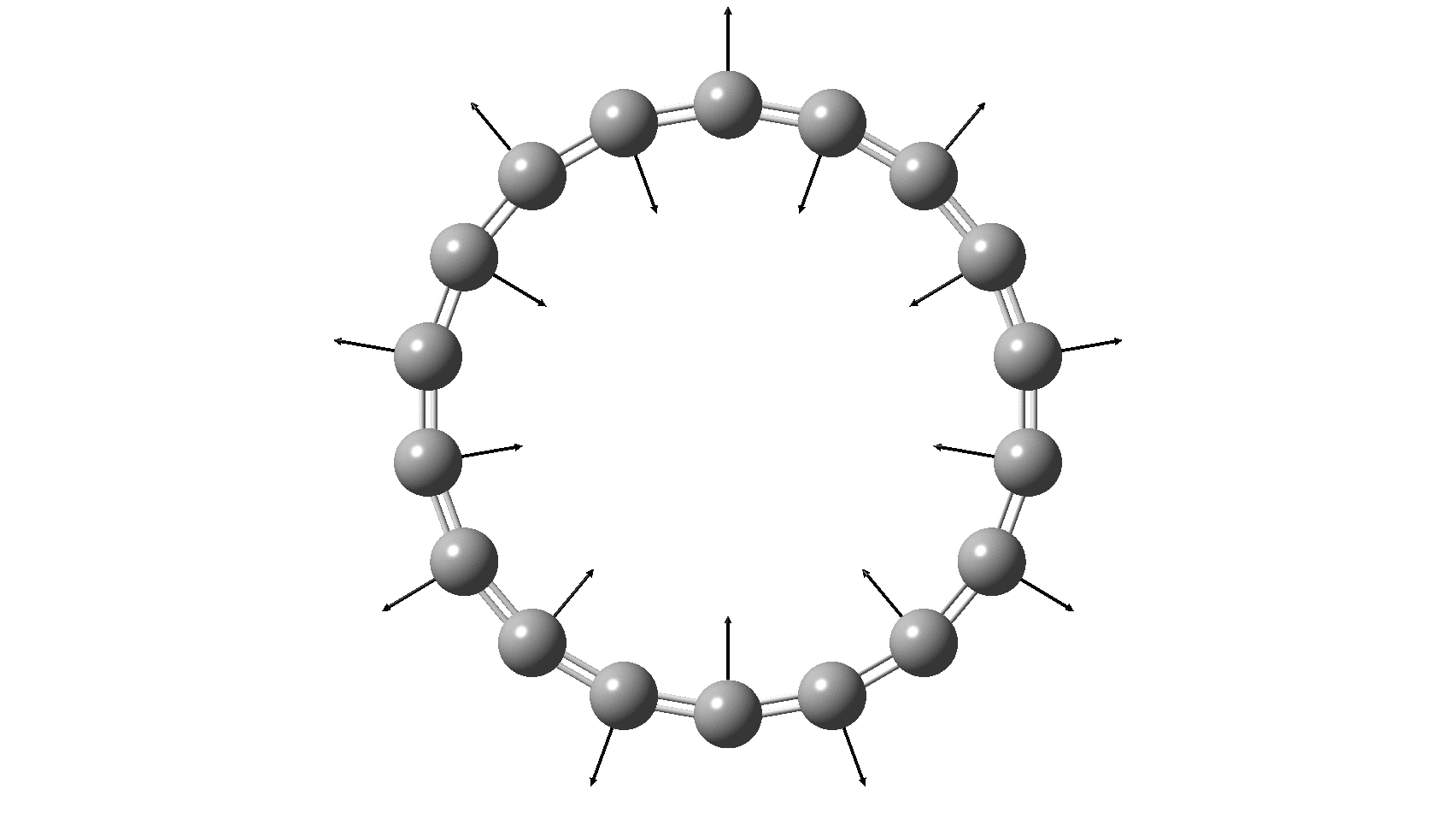
I have discussed the vibration in benzene known as the Kekulé mode in other posts, the first of which was all of ten years ago. It is a stretching mode that lengthens three of the bonds in benzene (a [6]-annulene) and shortens the other three, thus leading to a cyclohexatriene motif (see below). This vibration is real (+ve force constant) in benzene itself, which indicates that distorting the structure from six to three-fold symmetry leads to an increase in energy. Benzene therefore has a symmetrising influence, and it comes as a surprise to most to learn that this is actually due to the σ rather than the π-electrons! But there are good reasons to believe that as the ring size of the annulene increases, the Kekulé vibration will evolve from a real mode into an imaginary (-ve force constant) vibration representing a transition state for mutating the single and double bonds. At some point therefore, the more symmetrical geometry of the annulene in which all the bonds are of equal length will change into one of lower symmetry, in which BLA (bond length alternation) occurs and the symmetrical form becomes a transition state for this process.
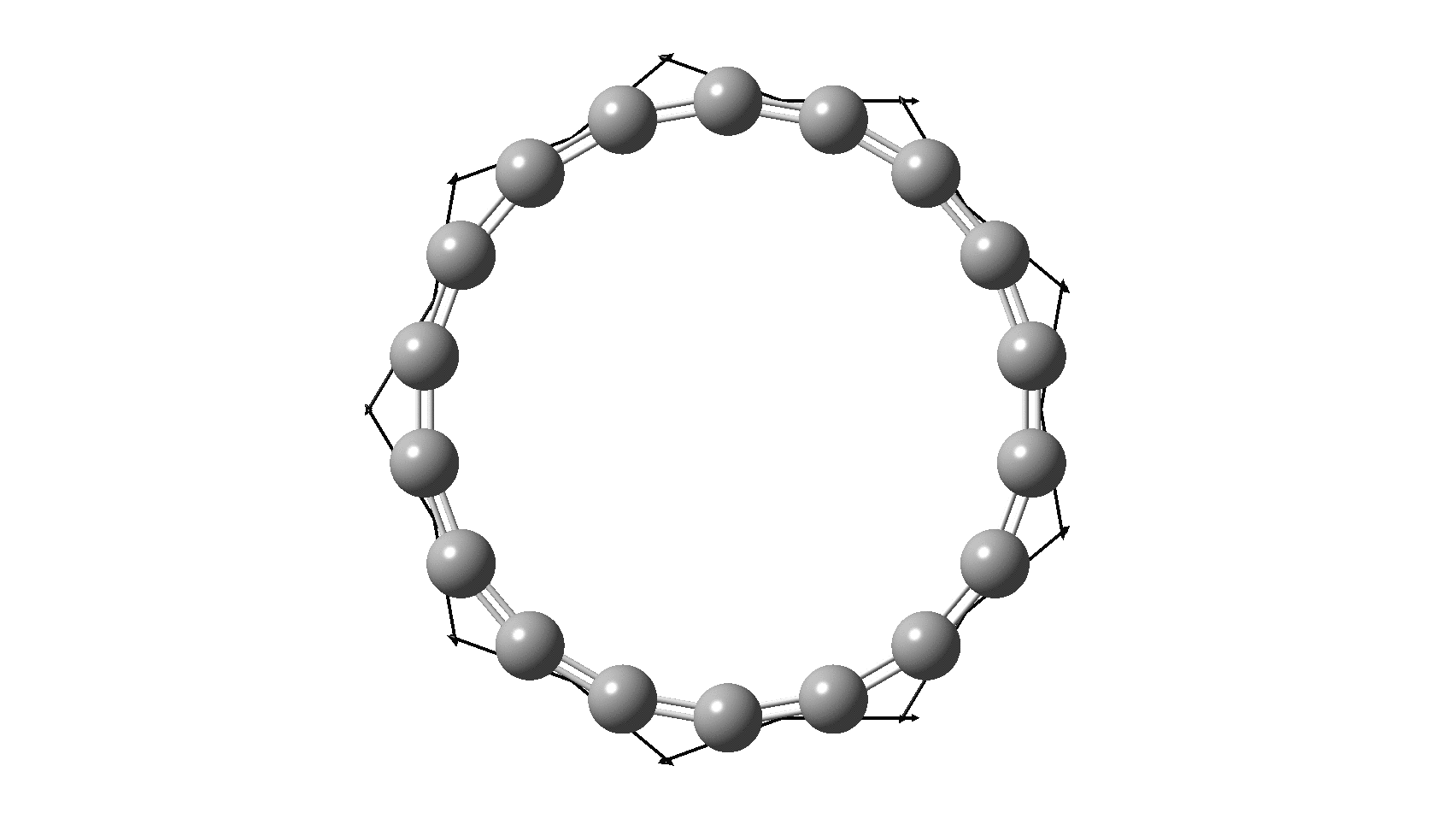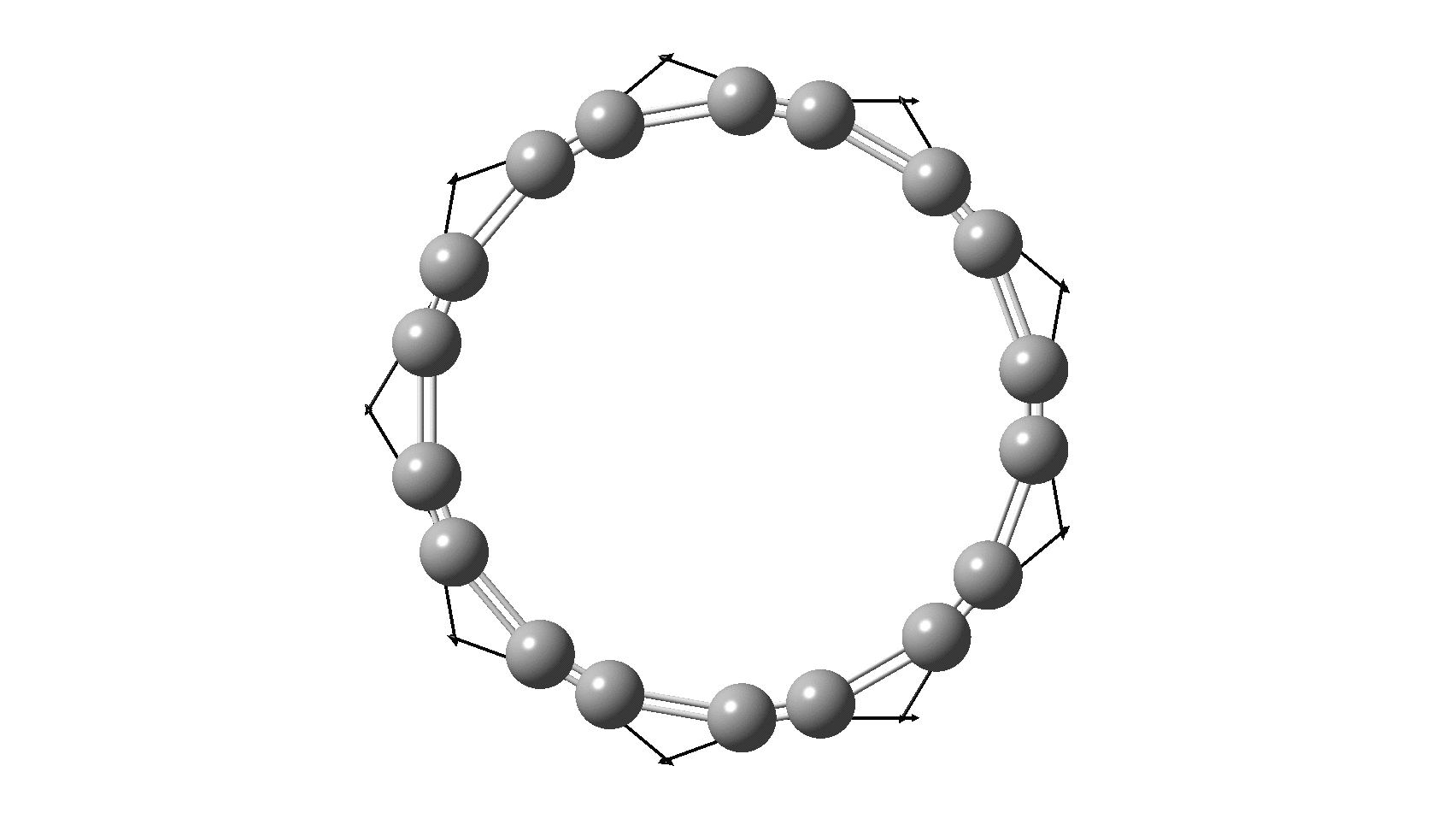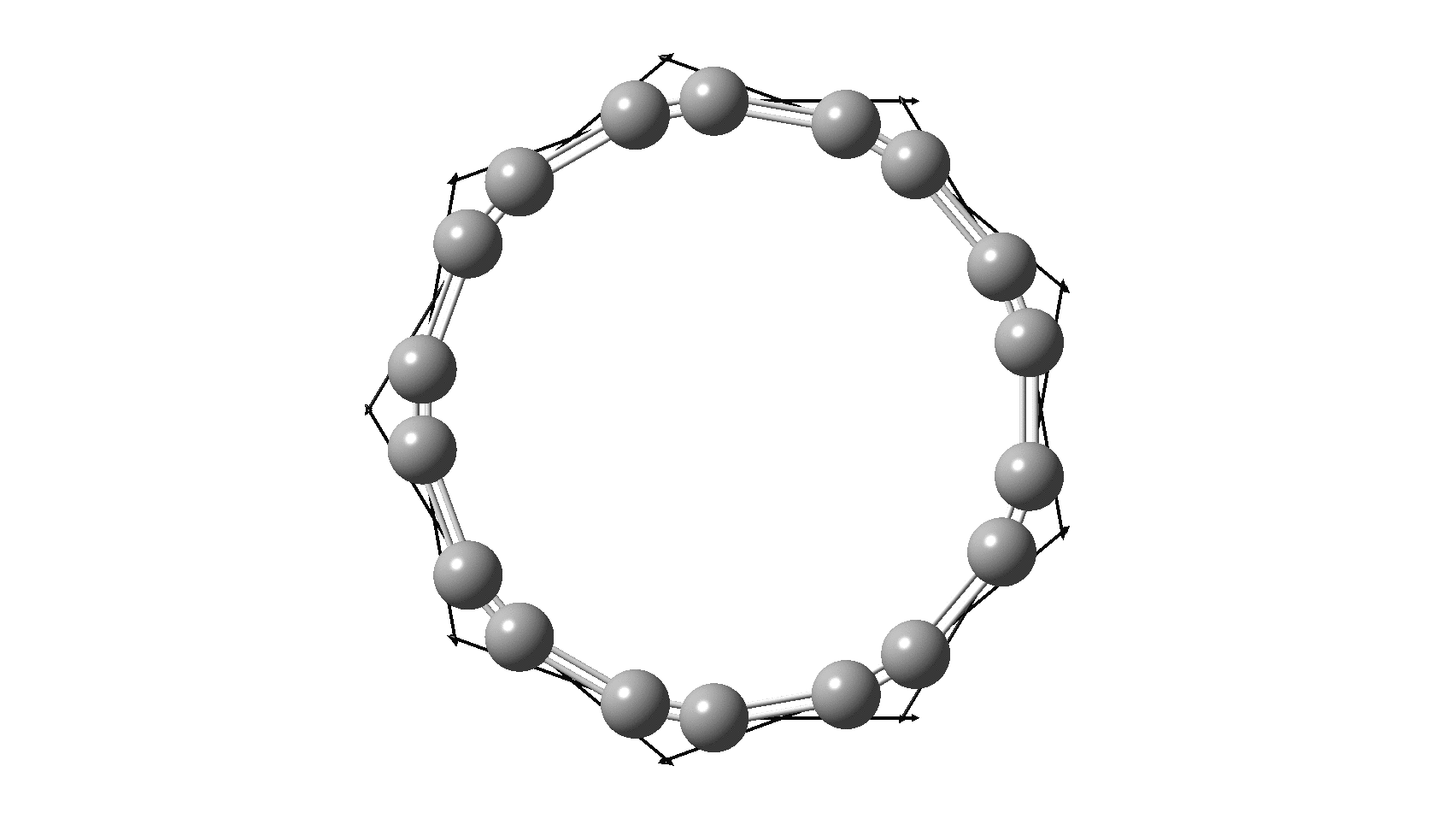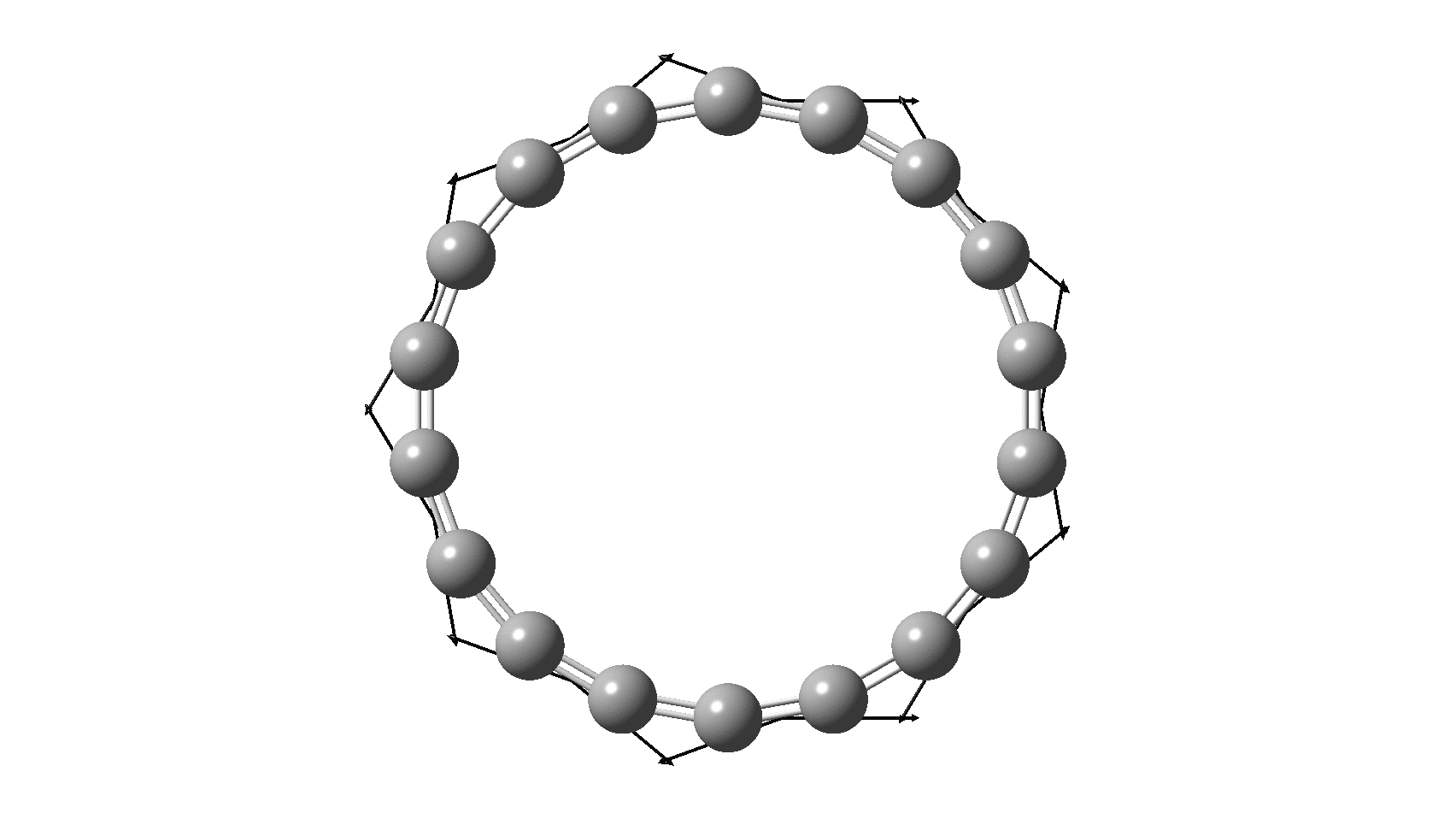
With this background, I noticed that a form of [18] annulene in which all the hydrogens have been removed (and is therefore another allotrope of carbon) has recently been synthesized and individual molecules studied on a metal surface using STM (a scanning tunnelling microscope).[cite]10.1126/science.aay1914[/cite] This allotrope is also of interest as a “double aromatic” molecule, with 4n+2 electron aromaticity arising from both the π and the σ system.
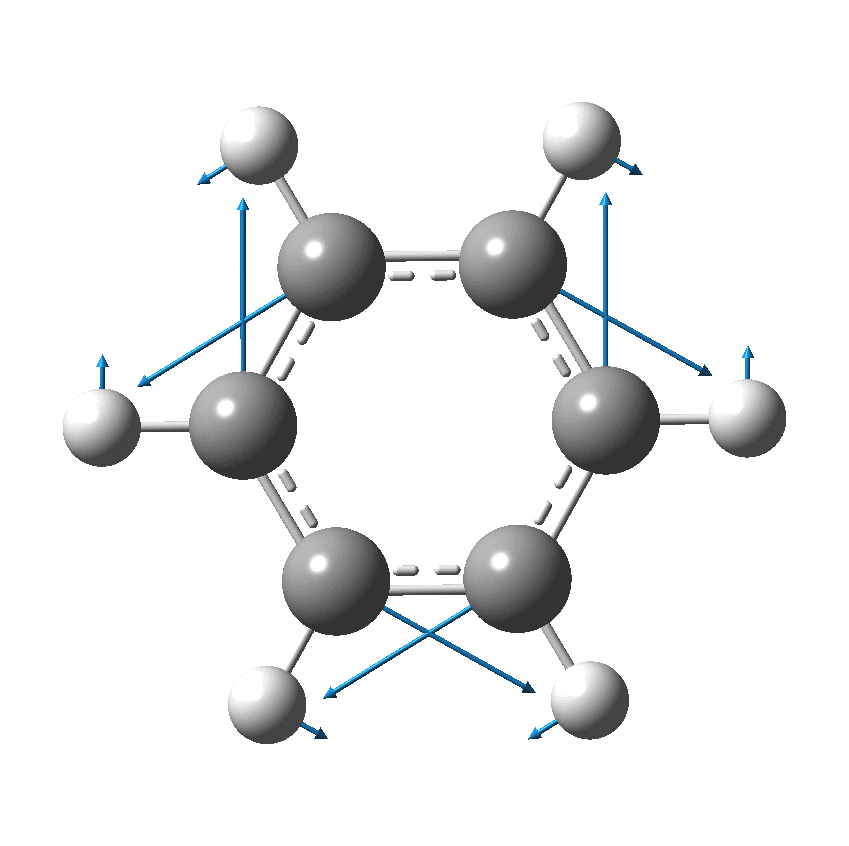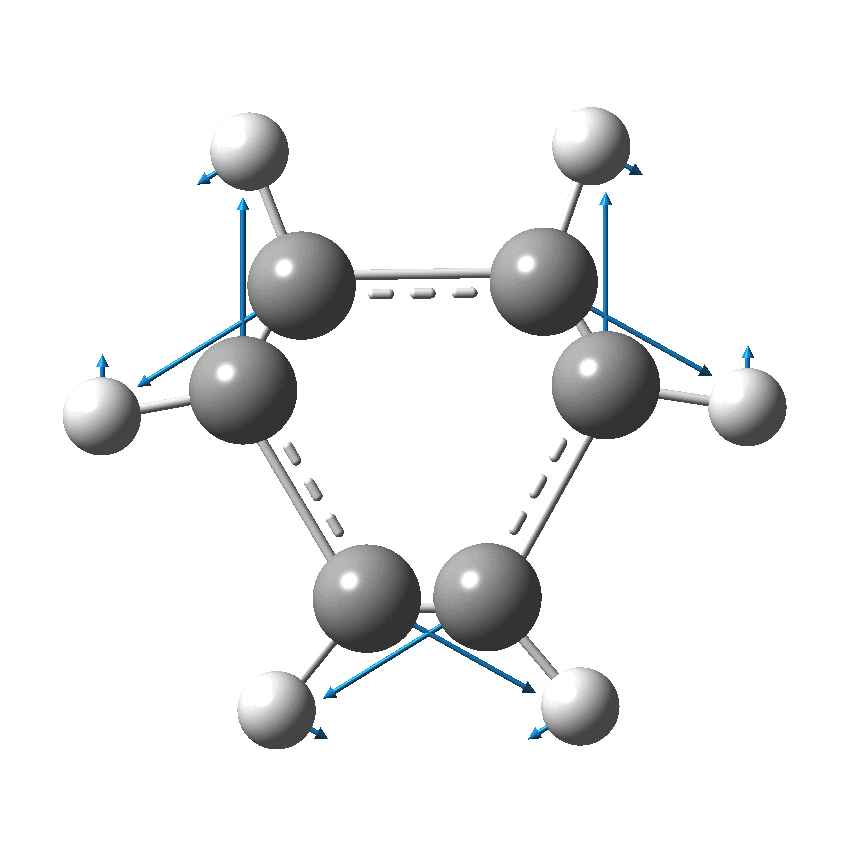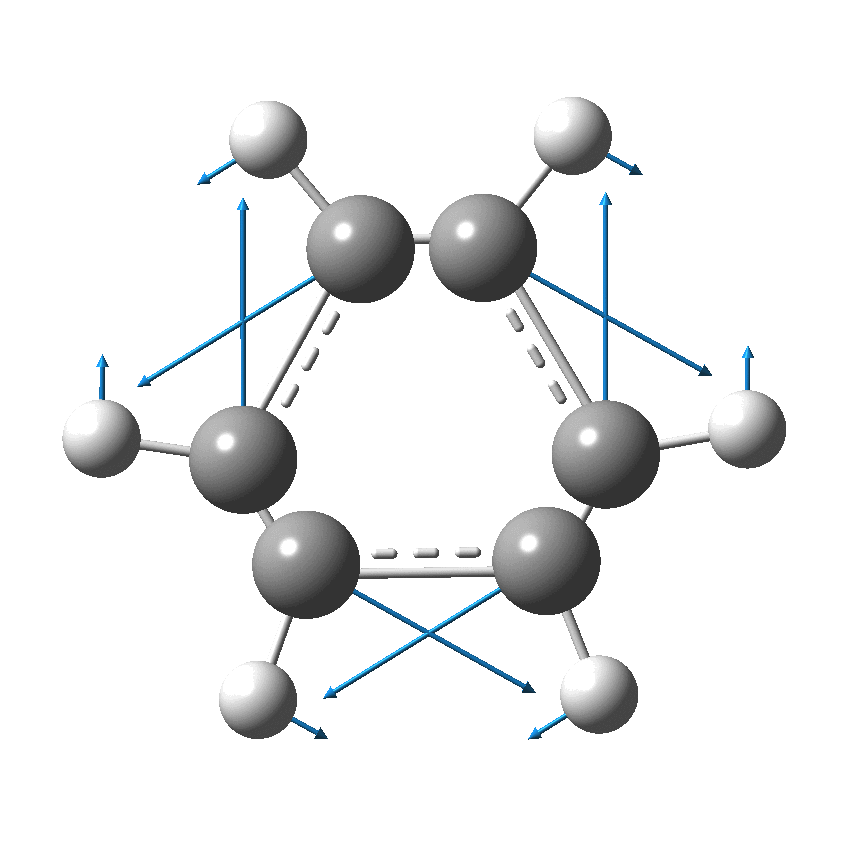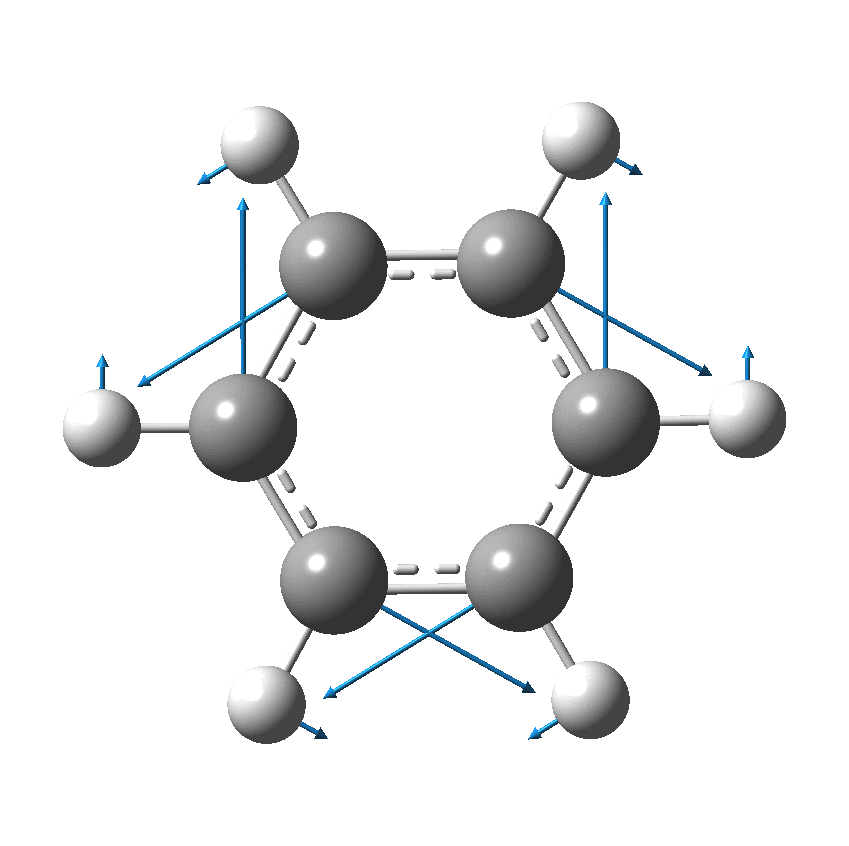
Cyclo[18]carbon, as this form is known, could have either 18-fold symmetry with no bond alternation, or 9-fold symmetry in which alternating short and long bond occur. The STM conclusions pointed to the form of structure with alternating bonds; these are attributed to triple and single in the article, but in fact no actual accurate bond lengths were (or can be) measured to directly support this.
I thought it might be interesting to see how various forms of computational quantum calculation might reflect this new experiment. In order to exploit the higher 18-fold symmetry to reduce calculation time, only the geometry with 18 equal bond lengths is computed here, along with the calculated value of the Kekulé mode. All the calculations are presented as FAIR data at DOI: 10.14469/hpc/6038
| Method | Kekulé mode, cm-1 | CC bond length, Å | Number of -ve force constants |
|---|---|---|---|
| Density functional methods | |||
| B3LYP+DG3+BJ/6-31G(d) | +766 | 1.284 | 5, all in-plane bucklings |
| B3LYP+DG3+BJ/6-311G(d) | +699 | 1.278 | 1, in-plane buckling |
| B3LYP+DG3+BJ/Def2-TZVPP | +673 | 1.276 | 0 |
| B3LYP+DG3+BJ/Def2-QZVPP | +649 | 1.275 | 0 |
| ωB97X-D/Def2-TZVPP | -2058 | 1.273 | 2, Kekulé + in-plane buckling |
| Double hybrid methods | |||
| B2PLYPD3/Def2-TZVPP | +2598 | 1.281 | 0 |
| DSDPBEP86/Def2-TZVPP | +3470 | 1.283 | 0 |
| PBEQIDH/Def2-TZVPP | +3447 | 1.277 | 0 |
| Møller-Plesset methods | |||
| MP2/6-31G(d) | +20444 | 1.295 | 8, in/out-of-plane buckling |
| MP2/6-311G(d) | +19885 | 1.293 | 8, in/out-of-plane buckling |
| MP2/Def2-TZVPP | +19466 | 1.289 | 0 |
| MP3/6-311G(d) | -15637 | 1.284 | 11, Kekulé + in/out-of-plane buckling |
| MP4(SDQ)/6-31G(d) | -9496 | 1.287 | 11, Kekulé + in/out-of-plane buckling |
| Coupled Cluster methods | |||
| CCSD/6-31G(d) | -4564 | 1.288 | 11, Kekulé + in/out-of-plane buckling |
| CCSD/6-311G(d) | -4310 | 1.286 | 11, Kekulé + in/out-of-plane buckling |
| CCSD(T)/6-31G(d) | N/A | 1.276 | N/A |
The conclusions include:
- The quality of the basis set is crucial. For lower quality bases, in-plane deformations of the ring occur, but the Kekulé mode itself is relatively unaffected. The minimum converged basis is Def2-TZVPP, which rather restricts the ability to perform higher level calculations.
- Even within the DFT methods, two popular functionals given diametrically opposite results. The B3LYP procedure predicts no BLA, whereas the alternative ωB97X-D functional suggests strong BLA. I could have proceeded through the functional zoo and added 100s more functionals to this list, but the point I wanted to make is already established!
- Double hybrid methods, which combine exact HF exchange with an MP2-like correlation, sometimes used as the next step up Jacob’s ladder, predict no BLA. With a very high real Kekulé mode (2600-3500 cm-1) they provide a first warning sign something is not quite right?
- Moller-Plesset expansions such as MP2 itself gives an unrealistic positive force constant for the Kekulé mode. The perturbation expansions are a notorious example that for a physically realistic result, the expansion has to converge and moreover is often assumed to converge rapidly. If the expansion is proven non-convergent, then neither the MP method itself, nor other methods which make use of it such as the double hybrid and the coupled cluster methods, can be trusted. For MP2 itself, the Kekulé mode has a value that indicates serious issues with the single-reference wavefunction used. The MP3 and MP4 expansions illustrate nicely the oscillation of the method.
- Coupled cluster methods, which also make use of MP expansions, are regarded as the next step up Jacob’s ladder. The computational cost of these scales so quickly that the larger basis sets are not feasible and so the (already proven as deficient) 6-31G(d) basis must be used. Again, we see the CCSD method mirroring the MP2-4 expansions.
So, are the MP and CCSD methods converging to a reliable solution, or are they oscillating too much to make any conclusions? If we think the convergence is approaching, then the Kekulé (transition state) mode for C18 (shown below) would indeed correspond to an interpretation of the STM observations as BLA.
But there might be an alternative explanation, that instead the molecule buckles in the manner illustrated below. This would also lead to 9-fold symmetry.
I conclude by pondering why the convergence of these methods is so strange. They are all single-reference methods, and perhaps C18 depends instead on multi-reference states? This would need a MCSCF (multi-configuration) or VB (valence bond) approach. Given the need for accurate basis sets, this is probably a big ask, but perhaps some group out there can do this and compare with the results here?