Ken Houk’s group has recently published this study of cycloaddition reactions, using a combination of classical transition state location followed by molecular dynamics trajectory calculations,[cite]10.1021/jacs.8b12674[/cite] and to which Steve Bachrach’s blog alerted me. The reaction struck me as being quite polar (with cyano groups) and so I took a look at the article to see what both the original[cite]10.1021/jo00042a039[/cite] experimental conditions were and how the new simulations compared. The reaction itself is shown below.
Turns out that chloroform was used as solvent (also benzene), whilst the transition state calculations and the subsequent molecular dynamics trajectories were modelled for the gas phase. The key observation is that if TS1 is used as the starting point for trajectory calculations, only 87% lead to the product predicted by classical transition state theory (3), as revealed by a classical intrinsic reaction coordinate (IRC) calculation. The remaining 13% lead to 4 and 5, the ambimodal effect. So here, I want to explore what effect including a continuum solvent on the computation of TS1 and its IRC might have on the classical (non-dynamic) model.
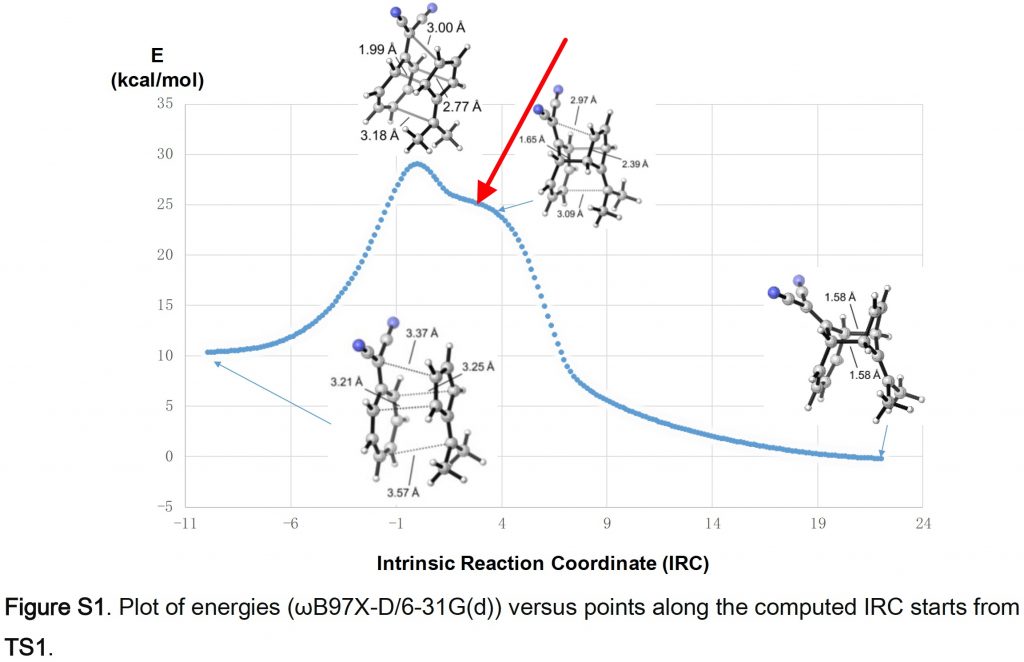
Firstly, the model for TS1 as reported[cite]10.1021/jacs.8b12674.[/cite], ωB97XD/6-31G(d) (FAIR data at DOI: 10.14469/hpc/5590). The basis set is modest by today’s standards, but is largely imposed by the need to use it for very large numbers of trajectory calculations. I was able to copy/paste the coordinates from the reported supporting information and then to replicate the IRC at this level (gas phase), also shown in the SI.
There is a feature in this IRC I want to expand upon (red arrow above). It occurs at an IRC value of ~-0.9 on the axis below.
It can be seen more clearly if the RMS gradient norm is plotted, the value of which drops to almost zero at IRC -0.9. Had it reached exactly 0.0, we would have had an intermediate formed. As it is we have what is called a hidden intermediate.
The origins of this intermediate can be more readily inferred from this dipole moment plot along the IRC. At TS1, the dipole moment is > 10D. A rule of thumb I have often used is that if a TS has a DM > 10, then one cannot ignore solvation any more and a gas phase model must be augmented.
Here are the same plots, but now with an added solvent field for water, an extreme polarity.
The IRC now stops at -2, being a high energy true (ionic) intermediate (rather than a hidden one). 
The IRC stops because gradient norm has now reached 0.0 at IRC -2, again an indication of a true intermediate. 
The dipole moment has been increased from 10 in the gas phase to around 15 at TS1 and it continues to increase until the ionic intermediate is reached. These differences from the gas phase plots are induced entirely by applying a continuum solvent model.
Next an intermediate solvent, chloroform, being one of the solvents used for the actual reaction. This time the gradient norm almost reaches a value of 0.0, avoiding it only by a whisker! A barely hidden intermediate.
The dipole moment totters around 13.5D, before finally collapsing as the ionic intermediate itself collapses to a neutral molecule again. Benzene as solvent (not shown here) reaches an intermediate dipole moment of about 12D. It too can stabilize an ionic intermediate noticeably even though it is not ionic itself.
I want to also briefly explore what effect if any the use of a relatively small basis set (6-31G(d)) has on the shape of the IRC. Below is a repeat of the gas phase IRC using the Def2-TZVPP basis, which is about twice the size of the smaller one (and hence is around 16 times slower to compute). The gradient norm shows that the “hidden intermediate” region around IRC -1 is a little more prominent (flatter).
So we see that both a solvent model (as a continuum field) and a larger basis set can increase the degree of “hidden intermediate” character in the classical reaction coordinate for this cycloaddition reaction, to the extent that if water is used as model solvent an actual discrete albeit shallow ionic intermediate forms. As Houk puts it, solvation induces a conversion from an entropic intermediate to an enthalpic one.[cite]10.1021/ja208779k[/cite] Molecular dynamics trajectories however have a propensity for not settling into quite shallow intermediates (those with escape barriers of < 3 kcal/mol, as would be the case here).
It will indeed be interesting to see the extent, if any, that either of the augmented models shown above affect the calculated distribution of molecular dynamics trajectories compared to those obtained using a gas phase model.
Tags: Chemistry, computational chemistry, Implicit solvation, Ken Houk, Molecular dynamics, Molecular modelling, Natural sciences, Physical sciences, Solutions, Solvent, Solvent model, Solvents, Steve Bachrach, Theoretical chemistry
What’s the predicted effect of an ionic liquid? If that gives an intermediate, perhaps a chiral ionic liquid would give 4 and 5 with enantiomeric enrichment.
The stabilizing effect on ionic intermediates is a very non-linear function of the dielectric of the medium. Thus increasing the dielectric from water to effectively infinity has actually a relatively small effect on the stabilization. Nonetheless, the effects of a chiral ionic solvent are indeed a very interesting question. I do know that chiral ionic liquids have been explored in this regard.