Previously, I explored (computationally) the normal vibrational modes of Co(II)-tetraphenylporphyrin (CoTPP) as a “flattened” species on copper or gold surfaces for comparison with those recently imaged[1]. The initial intent was to estimate the “flattening” energy. There are six electronic possibilities for this molecule on a metal surface. Respectively positively, or negatively charged and a neutral species, each in either a low or a high-spin electronic state. I reported five of these earlier, finding each had quite high barriers for “flattening” the molecule. For the final 6th possibility, the triplet anion, the SCF (self-consistent-field) had failed to converge, but for which I can now report converged results.†
| charge |
Spin Multiplicity |
ΔG, Twisted Ph, Hartree |
ΔG, “flattened”, Hartree |
ΔΔG, kcal/mol |
|---|---|---|---|---|
| -1 | Triplet | -3294.68134 (C2) | -3294.64745 (C2v) | 21.3 |
| -3294.616684 (C2v) | 40.6 | |||
| -3294.37012 (D2h) | 195.3 | |||
| Singlet | -3294.67713 (S4) | -3294.39418 (D4h) | 175.6 | |
| -3294.39321 (D2h) | 178.2 | |||
| -3294.56652 (D2) | 69.4 | |||
| FAIR data at DOI:10.14469/hpc/5486 FAIR data version of the tables in this and previous post at DOI:10.14469/hpc/5561 | ||||
I am exploring the so-called “flattened” mode, induced by the voltage applied at the tip of the STM (scanning-tunnelling microscope) probe and which causes the phenyl rings to rotate as per above. This rotation in turn causes the hydrogen atom-pair encircled above to approach each other very closely.‡ To avoid these repulsions, the molecule buckles into one of two modes. The first causes the phenyl rings to stack up/down/up/down. The second involves an all-up stacking, as shown below. Although these are in fact 4th-order saddle points as isolated molecules, the STM voltage can inject sufficient energy to convert these into apparently stable minima on the metal surface.
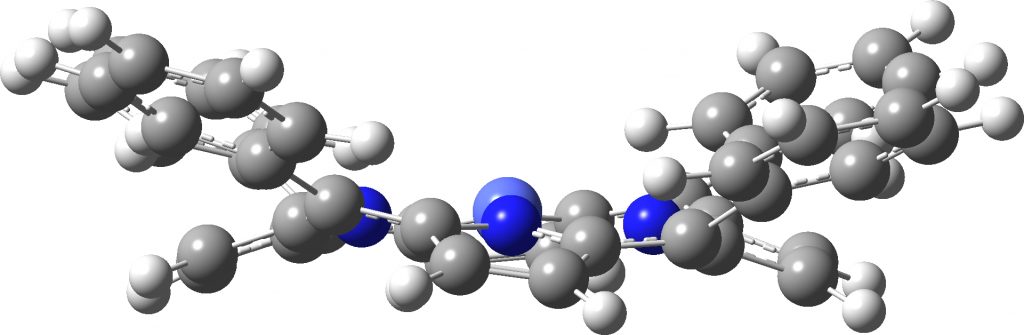
All syn mode, Triplet anion
The up/down/up/down “flattened” form (below) shows a much more modest planarisation energy than all the other charged/neutral states reported in the previous post, whereas the all-up isomer (which on the face of it looks a far easier proposition to come into close contact with a metal surface) is far higher in free energy.
The caption to Figure 3 in the original article[1] does not explicitly mention the nature of the metal surface on which the vibrations were recorded, but we do get “The intensity in the upper right corner of the 320-cm−1 map is from a neighbouring Cu–CO stretch” which suggests it is in fact a copper surface. Coupled with the other observation that in “contrast to gold, the Kondo resonance of cobalt disappears on Cu(100), suggesting that it acquires nearly a full electron from the metal (see Extended Data Fig. 2),” the model below of a triplet-state anion on the Cu surface seems the most appropriate.
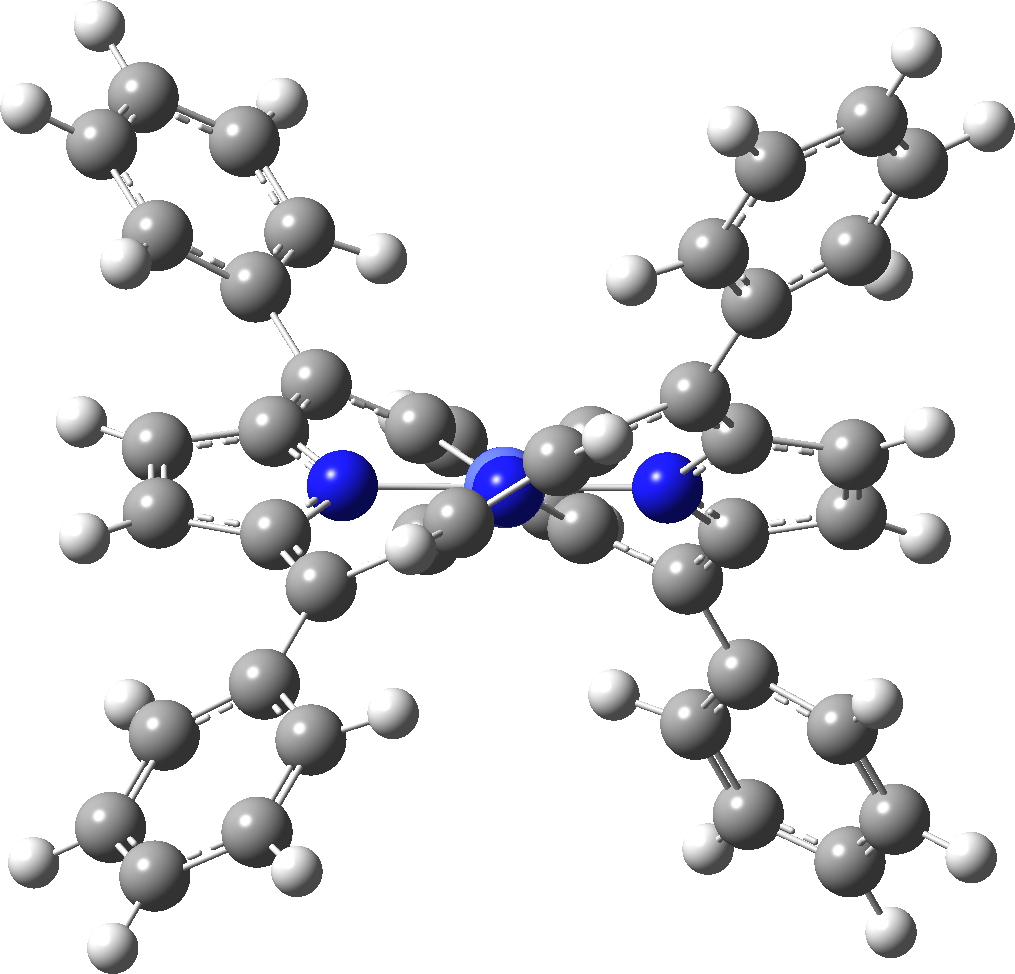
Syn/anti mode, Triplet anion with C2v symmetry
There is one final remark made in the article worth repeating here: “This suggests that the vibronic functions are complex-valued in this state, as expected for Jahn–Teller active degenerate orbitals of the planar porphyrin.26” Orbital degeneracy can only occur if the molecule has e.g. D4h point group symmetry, whereas the triplet anion stationary-point shown in the figure above has only C2v symmetry for which no orbital degeneracies (E) are expected. Enforcing D4h symmetry on Co(II) tetraphenylporphyrin results in eight pairs of H…H contacts of 1.34Å,‡ which is an impossibly short distance (the shortest known is ~1.5Å). Moreover this geometry has an equally impossible free energy 176 kcal/mol above the relaxed free molecule. Visually from Figure 3, the H…H contact distance looks even shorter (below, circled in red)! A D2h form (with no E-type orbitals) can also be located.
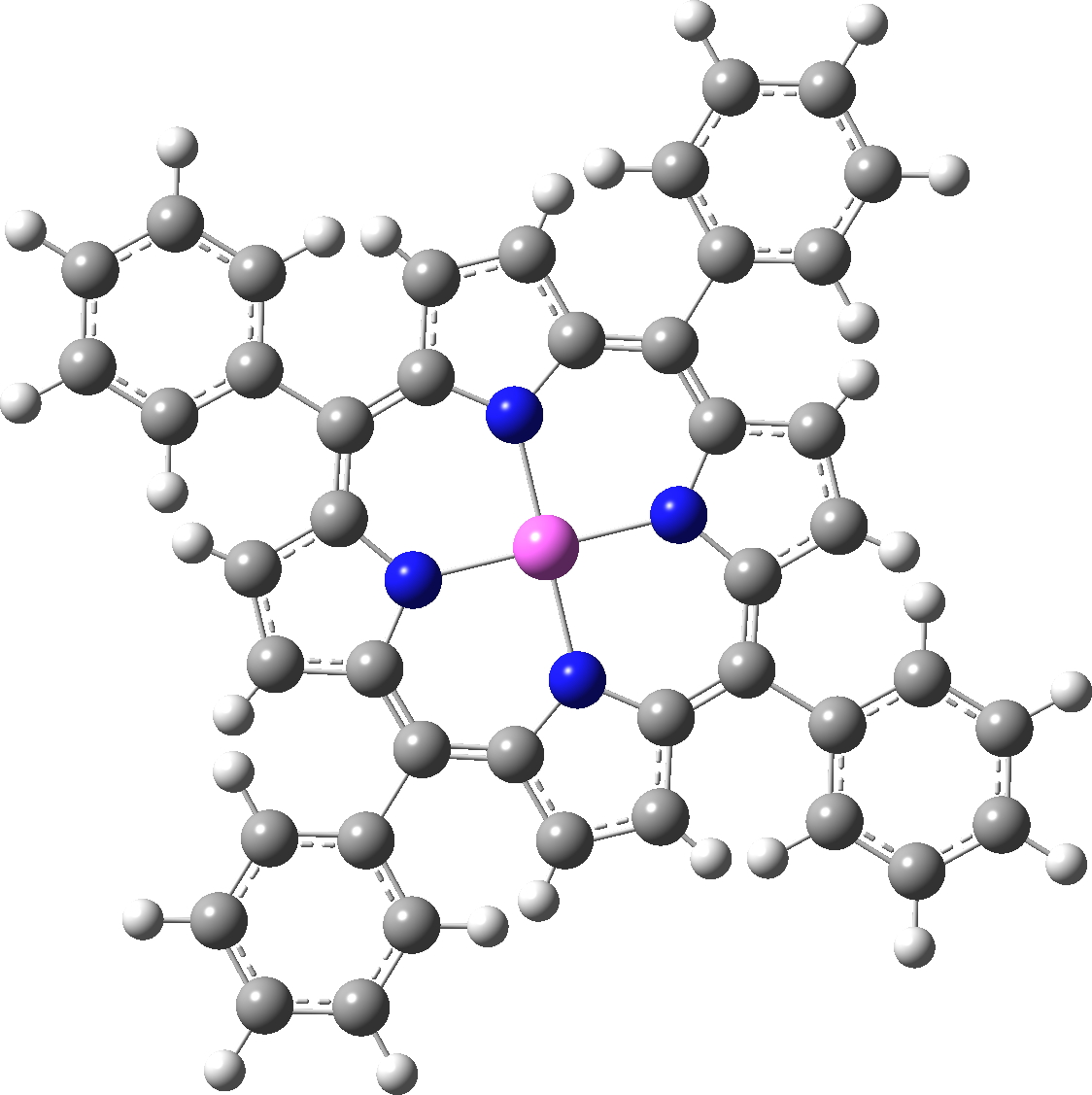 Singlet, Calculated with D4h symmetry. Click for vibrations. |
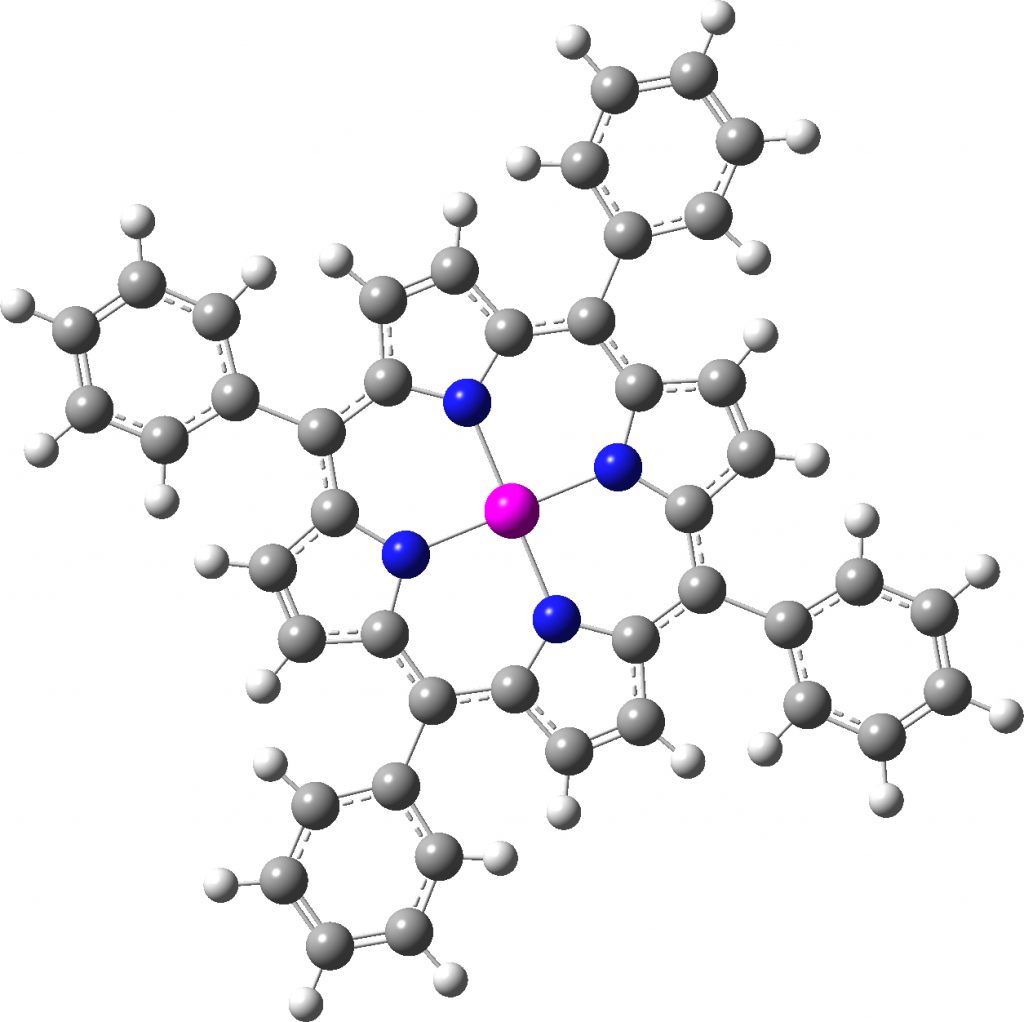 Singlet, Calculated with D2h symmetry. Click for vibrations. |
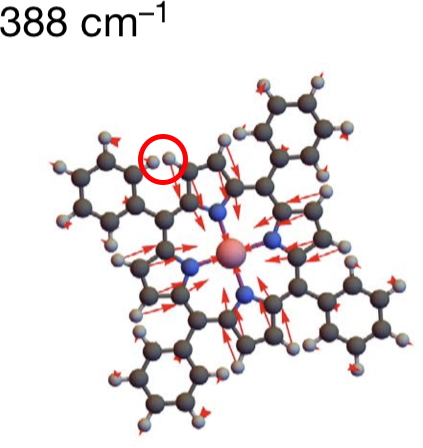 Taken from Figure 3 (Ref 1). |
|
These totally flat species are calculated to be at 13 or 12th-order saddle points, with the eight most negative force constants having vectors which correspond to up/down avoidance motions of the proximate hydrogen pairs encircled above and the remaining being buckling modes of the entire ring.
So to the mystery, being the nature of the “flattened” CoTPP on the copper metal surface, as represented in Figure 3 of the article.[1] Is it truly flat, as implied by the article? If so, the energy of such a species would be beyond the limits of what is normally considered feasible. Moreover, it would represent a species with truly mind-blowing short H…H contacts. Or could it be a saddle-shaped geometry, where the phenyl rings are not lying flat in contact with the metal but interacting via the phenyl para-hydrogens? That geometry has not only a much more reasonable energy above the unflattened free molecule, but also acceptable H…H contacts (~2.0.Å) However, would such a shape correspond to the visualised vibrational modes also shown in Figure 3? I have a feeling that there must be more to this story.
†These convergence problems were solved by improving the basis set via adding “diffuse” functions, as in (u)ωB97XD/6-311+G(d,p). Convergence to the lowest energy electronic state (3B2) is achieved using a Huckel initial guess rather than the default Harries, which gives the higher energy 3A2. ‡If the crystal structure for these species is flattened without geometry optimisation, the H-H distance is around 0.8Å ♥This blog has a DOI: 10.14469/hpc/5559.
References
- J. Lee, K.T. Crampton, N. Tallarida, and V.A. Apkarian, "Visualizing vibrational normal modes of a single molecule with atomically confined light", Nature, vol. 568, pp. 78-82, 2019. https://doi.org/10.1038/s41586-019-1059-9
Tags: 019-1059-9, 10.1038, Biomolecules, Chelating agents, chemical bonding, Chemical compounds, Chemistry, Coordination chemistry, Coordination complex, Copper, copper metal surface, Cu–CO, E-type, energy, free energy, higher energy, impossible free energy, Inorganic chemistry, Jahn–Teller effect, lowest energy electronic state, Metabolism, metal, metal surface, modest planarisation energy, Molecule, Natural sciences, Physical sciences, planarisation, Porphyrin, reasonable energy, Resonance, Solid-state chemistry, sufficient energy, Teller, Tetraphenylporphyrin
Here are two searches of the Cambridge crystal database. The first is for H…H distances in tetraphenyl porphyrins (any transition metal) between adjacent phenyl rings in the ortho positions. The second is the torsion angle between a phenyl group and the porphyrin ring between adjacent phenyl rings.
The shortest H…H distances are about 2.4Å. The torsions are about 70/110°, with a few structures where the angles are closer to 90°.
Nothing unusual here, and especially no sign of unusual short H…H contacts.