I noted in my WATOC conference report a presentation describing the use of calculated reaction barriers (and derived rate constants) as mechanistic reality checks. Computations, it was claimed, have now reached a level of accuracy whereby a barrier calculated as being 6 kcal/mol too high can start ringing mechanistic alarm bells. So when I came across this article[1] in which calculated barriers for a dyotropic ring expansion observed under mild conditions in dichloromethane as solvent were used to make mechanistic inferences, I decided to explore the mechanism a bit further.
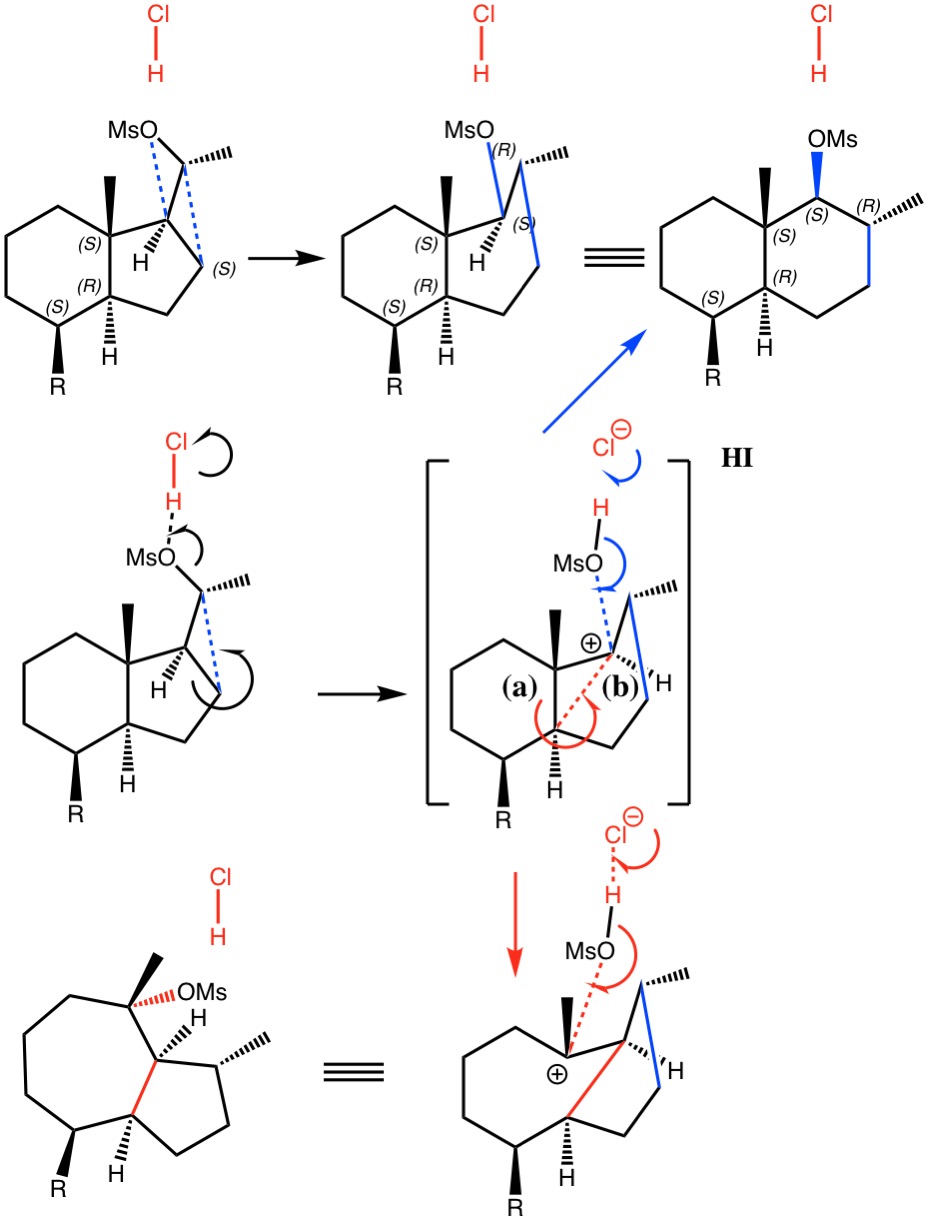
Shown in blue above is the reported outcome, a dyotropic transposition of a OMs group with a ring CH2 group. Shown in red are my additions.
The observed product is a 6,6-bicyclic ring system, for which various calculated mechanistic pathways were reported (R=H)[1].
- The first involved dyotropic-like [1,2] transposition of the neutral molecule, for which barriers >39 kcal/mol were calculated[1]. These are certainly too high to be viable and the warning bells were certainly heeded.
- These bells led the authors to the hypothesis that protonation of the OMs group would facilitate the reaction (Figure 7[1]). Their model included the proton, but did not include any counter-ion. A barrier of 5.6 kcal/mol for this system was estimated and considered “fully compatible with the mild experimental conditions“. However, as they also noted, “a singular transition structure could not be located due to the topology of the potential energy surface” and “A nudged elastic band method (was) employed to explore how the reaction proceeds“. This latter method was new to me, but in fact since I now thought the barrier might be too low; warning bells started to ring for me now.
- I thought the answer might relate to the lack of a negative counter-ion to the positive proton and so I added HCl instead of H+ (red above) to create a more physically realistic model of an acid catalyst; an isolated cation is an un-physical model, unless found in e.g. a mass spectrometer. Also included were two explicit water molecules, waters that were also included in the reported models[1], to help stabilise what was likely to be an ion-pair like system, labelled HI in the diagram above. I will explain what HI means shortly.
- I used the same ωB97XD/Def2-SVPP/SCRF=DCM method as originally reported[1]. The inclusion of explicit HCl instead of H+ now readily allowed a transition state to be located and an IRC (intrinsic reaction coordinate) could be computed (FAIR data DOI: 10.14469/hpc/3016) as a replacement for nudged elastic bands! This profile turned out to have some remarkable features, as I will discuss below.
- I also recomputed the reactant and transition state at the Def2-TZVPPD basis set level, which allows for a better description of negative ions (FAIR data DOI: 10.14469/hpc/3095,10.14469/hpc/3140) and this results in a calculated ΔG‡195 of ~16 kcal/mol, less than the original computed transition state barriers of >39 kcal/mol and closer to the barrier required for mild experimental conditions at -78°C.
- An animation of the IRC at the ωB97XD/Def2-SVPP/SCRF=DCM level (10.14469/hpc/3016) is shown below. It is a concerted formally dyotropic process, albeit very asynchronous in nature in which C-OMs bond breaking precedes C migration, which in turn precedes C-OMs bond formation.
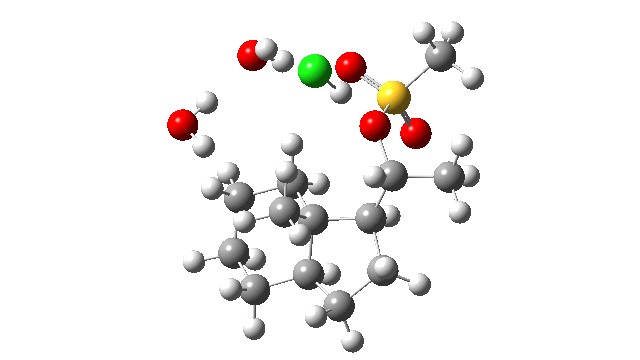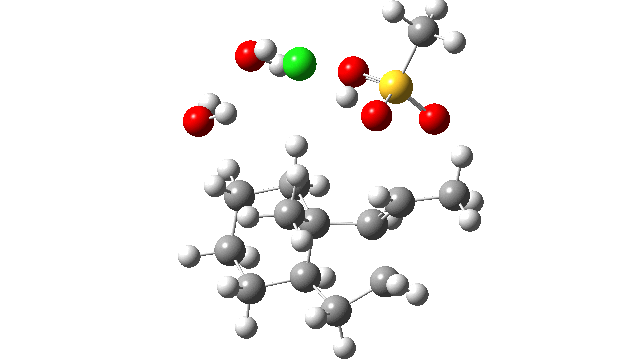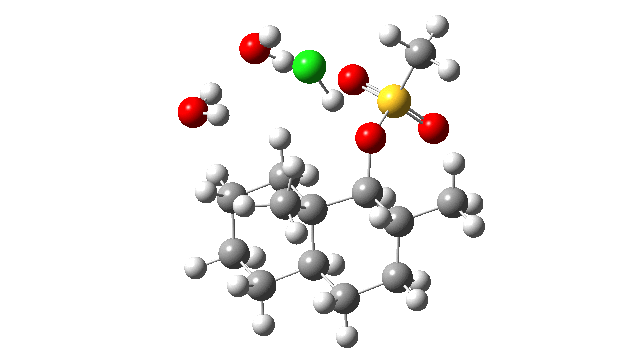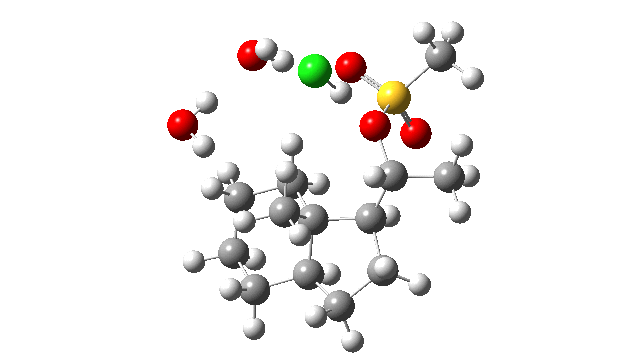
- The energy profile is shown below.
- Between IRC -13 and IRC -6, the reaction prepares for a proton transfer from HCl to the mesityl oxygen, which occurs ~IRC -4.
- From IRC -3 to IRC +1, the profile is very flat, which probably is the cause of the original failure[1] to locate a transition state.
- The region IRC -3 to +2 is where the CH2 group starts to migrate, reaching the half way point at ~ IRC 0, the transition state.
- At IRC +4, the alkyl [1,2] migration is complete and a hidden ion-pair intermediate has formed.
- From IRC +5 to +17, this hidden ion-pair collapses to form the final non-ionic product. In the process a second proton transfer occurs back to the chloride anion (~IRC +5).
- The hidden ion-pair intermediate can be seen more clearly in this plot of the energy derivative gradient norm at IRC +4. The two proton transfers can be seen very clearly as sharp features at IRC -4 and +5.
- The zone of the hidden ion-pair intermediate can also be seen in this dipole moment plot.
- This next plot charts the changes in the length of the bond labelled (a) in the diagram above. As the CH2 migration starts to create a carbocation-mesityl anion pair, the bond connecting the two rings is now tempted to also migrate. Doing so would create a more stable tertiary carbocation centre.
- This is mirrored by the length of the bond labelled (b). As (a) lengthens, so (b) contracts. But then at IRC +4, the aspirations of both bonds are cruelly frustrated. The methane sulfonic acid has just lost its proton (which has returned to its original home, the chloride anion) and, as an anion, is now voraciously seeking a cation. It out-competes bond (b) and forms a C-O bond. The rejected bond (b) rapidly retreats.
- The knock-on effects of this battle between two electron donors can be see further afield. Here is a plot of one C-H bond length (shown above as R-C; R=H). In the expectation that bond (b) will depart, it starts to increase its hyperconjugation with the adjacent carbon, but then retreats along with bond (b).
There are lots more fun to be had with these IRC plots, but I will stop there and try to summarise. This [1,2] dyotropic transposition only has a reasonably low barrier if an ion-pair can be formed. This in turn requires a proton as catalyst, which starts off life attached to Cl, then migrates to O to enhance the ion-pair formation, and finally returns back home to the Cl. By using just a proton (without chloride) in the original study[1], in effect only the region of the reaction coordinate not involving the proton transfers was studied, i.e. IRC -4 to IRC +5. That would indeed give the misleading impression of a very small barrier for the reaction. By including a larger region of the reaction coordinate with the addition of chloride, we get a more realistic model for the reaction.
More importantly, we learn a lot more about the reaction from this better model. The most important new insights are:
- Beyond the transition state at IRC = 0, we have pathways for both the formation of a 6,6 bicyclic ring (the blue route in the scheme above) and an alternative 5,7 bicyclic ring product (red route above). The 6,6 product was isolated in 70% yield, which leaves open the possibility that some 5,7 product was formed but was not identified. It would be worth repeating the original synthesis to see if any such product could in fact be detected.
- The fact that remote substituents such as R have a response to the reaction suggests that they could be used to mediate between 6,6 and 7,5 ring formation. Perhaps some modification could be found that would lead to only 5,7 product? I will explore this computationally and report my results back presently.
- This may represent yet another example where reaction dynamics play a role in determining the product outcome. One transition state but two possible products! So, as also noted in the previous post, yet another candidate for a molecular dynamics study?
References
- H. Santalla, O.N. Faza, G. Gómez, Y. Fall, and C. Silva López, "From Hydrindane to Decalin: A Mild Transformation through a Dyotropic Ring Expansion", Organic Letters, vol. 19, pp. 3648-3651, 2017. https://doi.org/10.1021/acs.orglett.7b01621
Tags: animation, bicyclic ring product, energy derivative gradient norm, energy profile, final non-ionic product, Organic chemistry, possible products, potential energy surface, realistic model for the reaction
A note on basis sets. In the IRC above, I used the Def2-SVPP basis originally reported, and then a Def2-TZVPPD basis to compute the activation free energy. Here I fill the gap in with results for the Def2-SVPD basis. This includes diffuse functions which are better suited for describing the negatively charged chloride anion. The addition of such functions to the SVPP basis significantly lower the activation free energy by stabilizing the ion-pair-like transition state. The triple-ζ basis shows a further modest improvement. A likely estimate of a CBS (complete basis set) limit is probably ~15.0-15.5 kcal/mol.
Basis set ΔG195‡, kcal/mol Def2-SVPP 21.6 Def2-SVPD 16.5 Def2-TZVPPD 15.8A further correction can be added to the calculated free energy barrier. This relates to the molecularity of the reaction (bimolecular) and the standard state (see DOI: 10.1021/ol060261z). The standard state for the system as quoted above is 1 atmosphere. A more reasonable standard state for a reaction conducted in solution is 1M, and at 195K, the conversion factor is 16.0 (in other words 1 atm ≡ 0.0625M). This propagates through as a reduction in the barrier of 1.1 kcal/mol, reducing it to ~14.7 kcal/mol (at 195K), or probably a little lower if estimating the CBS (complete basis set) limit.
Using the relation Ln(k/T) = 23.76 – ΔG‡/RT and an estimated lower bound for the activation energy of 14.0 kcal/mol (for a 1M standard state), gives a half life of ~ 1744 seconds, or half an hour at 195K.