Early in 2011, I wrote about how the diatomic molecule Be2 might be persuaded to improve upon its normal unbound state (bond order ~zero) by a double electronic excitation to a strongly bound species. I yesterday updated this post with further suggestions and one of these inspired this follow-up.
The standard molecular orbital diagram for Be2 below shows two electrons in both the 2s Σg and Σu levels, the first being considered bonding and the second antibonding. By exciting the two electrons from the Σu into the Πu MO to form a triplet, one converts one antibonding occupancy into two bonding occupancies, in the process changing the total formal bond order from zero to two.
You can see the results of my playing with these ideas both in my appended comments to the original post and the table below. This shows that the calculated bond order for the excited triplet state of Be2 is actually closer to 1.50 rather than to two, but definitely not zero!
| System | Wiberg bond order | Bond length | FAIR Data |
|---|---|---|---|
| Be2 singlet | 0.15 | 2.805 | 10.14469/hpc/3082 |
| Be2 excited triplet | 1.50 | 1.785 | 10.14469/hpc/3075 |
| Be22+ | 1.00 | 2.135 | 10.14469/hpc/3076 |
| Be22- triplet | 0.89 | 2.242 | 10.14469/hpc/3074 |
| Be22- excited singlet | 3.00 | 1.817 | 10.14469/hpc/3083 |
The games above represent isoelectronic substitutions and here I try one more, namely that Li22- is isoelectronic with Be2. Unlike the latter, there is no need to force an electronic excitation (ωB97XD/Def2-QZVPPD/SCRF=water) to achieve the required occupancies with Li22-.
| System | Wiberg bond order | Bond length | FAIR Data |
|---|---|---|---|
| Li22- triplet | 1.501 | 2.381 | 10.14469/hpc/3087 |
I also checked what crystal structures could tell us about Li-Li bonds and it seems 2.38Å is about as short as they get. 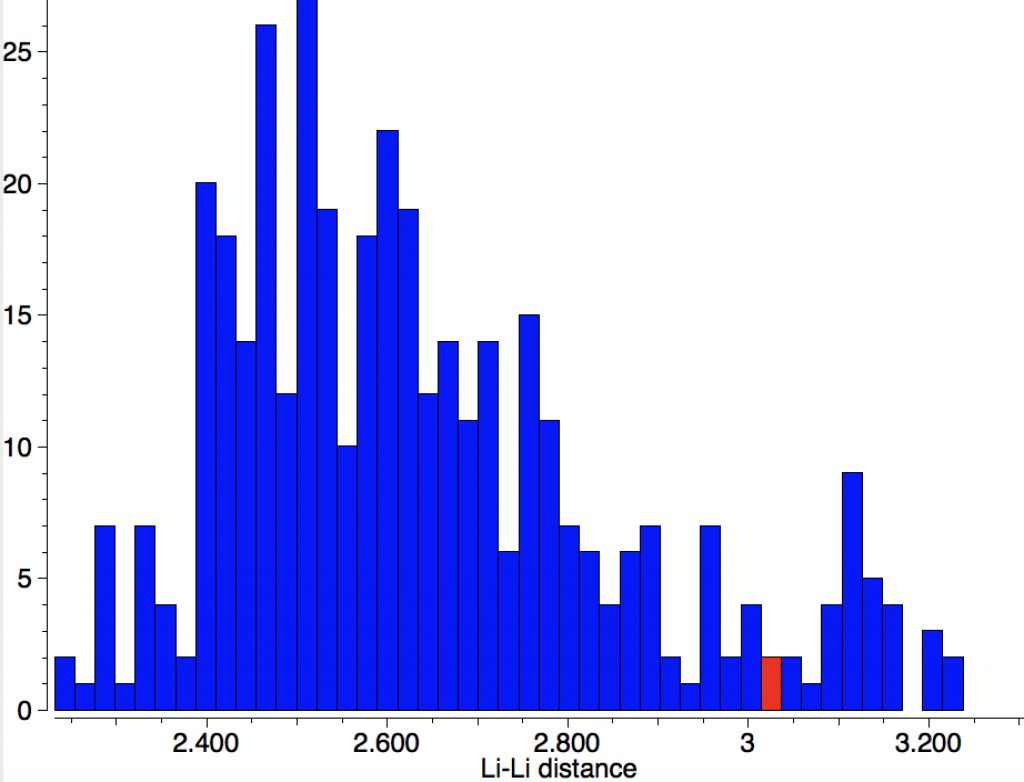
At this point, the NBO analysis of the Li22- localised orbitals alerted me to another feature, which is that the Rydberg occupancy amounted to 2.18e. This in turn reminded me of the previous post which dealt with such occupancy in another small molecule, CH3F2-, but here the Rydberg occupancy involved the 3s/3p AOs of the carbon and the fluorine. With Li22- triplet, it is of the lithium 2p AO (2.18e) and only a tiny occupancy of 3d (0.03). By definition, for alkali metals such as Li the normal valence shell is just 2s, whereas 2p occupancy is considered a Rydberg state; a hypervalent state if you will. So Li22- triplet has a Li-Li hyper-bond!‡ Of course, by this definition most Li compounds are then hypervalent, since many have populated 2p shells.
Even if use of the term hyper-bond to describe Li22- triplet is rather artificial, this example does reveal the games one can play with the first row elements Li-B (see table above). Given that most introductory text books on bonding normally only explain the diatomics formed from N-Ne (occasionally including C), I might suggest that these earlier elements are equally instructive and fun to play with.
‡ This species is 36.0 kcal/mol higher in free energy than two separated Li– anions.
Tags: Be-Be double bond, Be-Be triple bond, Chemical bond, Chemistry, Cs-Cs double bond, Diatomic molecule, free energy, General chemistry, K-K double bond, Li-Li double bond, Molecular geometry, Oxygen, Province/State: Be2, Quantum chemistry, Rb-Rb double bond, Stereochemistry

Here are two variations on the theme, LiB2- and LiBe1-.
Both are ionic, with small bond orders and hence quite different from the homonuclear diatomics.
Here is 3Σg Cs22- (ωB97XD/Def2-QZVPPD). The bond length is 4.396Å, ν 69 cm-1 and the Wiberg bond order is 1.504 with a Rydberg population of 2.238e (DOI: 10.14469/hpc/3091). The natural electron configuration is
Cs: [core]6S(0.88)5d(0.39)6p(0.72)
which shows both p and d-expansion of the S shell. This species is 20.4 kcal/mol higher than separated Cs– ions.
Now 3Σg Rb22- (ωB97XD/Def2-QZVPPD). The bond length is 4.207Å, ν 67 cm-1 and the Wiberg bond order is 1.502 with a Rydberg population of 2.26e (DOI: 10.14469/hpc/3097). The natural electron configuration is
Rb: [core]5S(0.87)4d(0.25)5p(0.88)4f(0.01)
Now 3Σg K22- (ωB97XD/Def2-QZVPPD). The bond length is 3.847Å, ν 105 cm-1 and the Wiberg bond order is 1.502 with a Rydberg population of 2.25e (DOI: 10.14469/hpc/3098). The natural electron configuration is
K: [core]4S(0.88)3d(0.18)4p(0.94)
Here are four more systems, Mg22--Ba22-
The Rydberg occupancies are:
Be: [core]2S(0.95)2p(2.04)4p(0.01)
Mg: [core]3S(0.98)3p(2.01)3d(0.01)4p(0.01)
Ca: [core]4S(0.97)4p(1.94)3d(0.09)
Sr: [core]5S(0.97)5p(1.96)4d(0.07)
Ba: [core]6S(0.99)6p(2.01)
All these systems exhibit two π-hyper-bonds each, and a normal σ-bond (assuming the definition of the p-shells as Rydberg levels).