Layer stacking in structures such as graphite is well-studied. The separation between the π-π planes is ~3.35Å, which is close to twice the estimated van der Waals (vdW) radius of carbon (1.7Å). But how much closer could such layers get, given that many other types of relatively weak interaction such as hydrogen bonding can contract the vdW distance sum by up to ~0.8Å or even more? This question was prompted by the separation calculated for the ion-pair cyclopropenium cyclopentadienide (~2.6-2.8Å).
The search query for the Cambridge structure database is shown below.
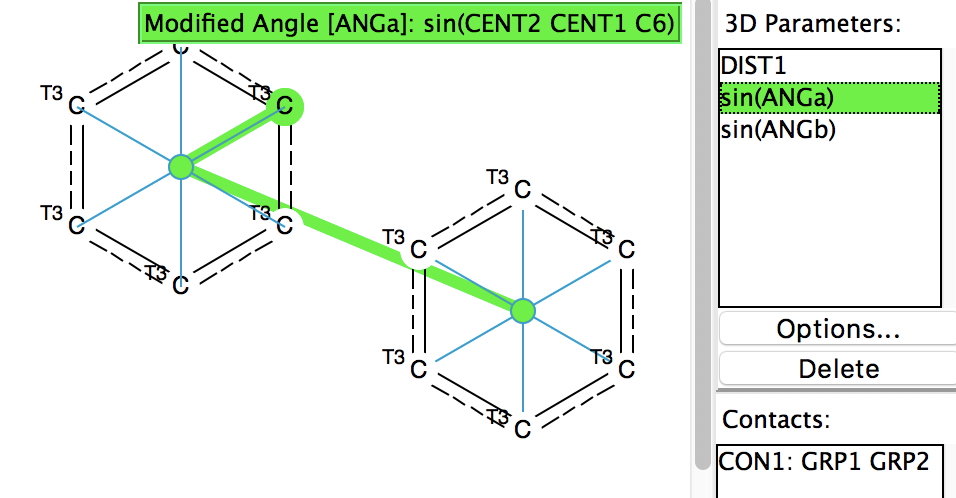
The query (dataDOI: 10.14469/hpc/2471) defines centroids for two benzenoid rings, both comprising only 3-coordinated carbons. The sine of an angle subtended at each centroid to the other and to one ring carbon attempts to track how parallel the two rings are (strictly speaking, 12 such angles should be included). If the sines of both angles are 1.00, then the two centroids overlap orthogonally. A search constrained to no disorder, no errors and R < 0.05 reveals 1107 hits at a centroid-centroid distance of < 3.5Å. The colour code (red) indicates the distances in the range 3.4-3.5Å, which matches that of graphite, while distances down to 3.2Å (yellow-green) are not uncommon.
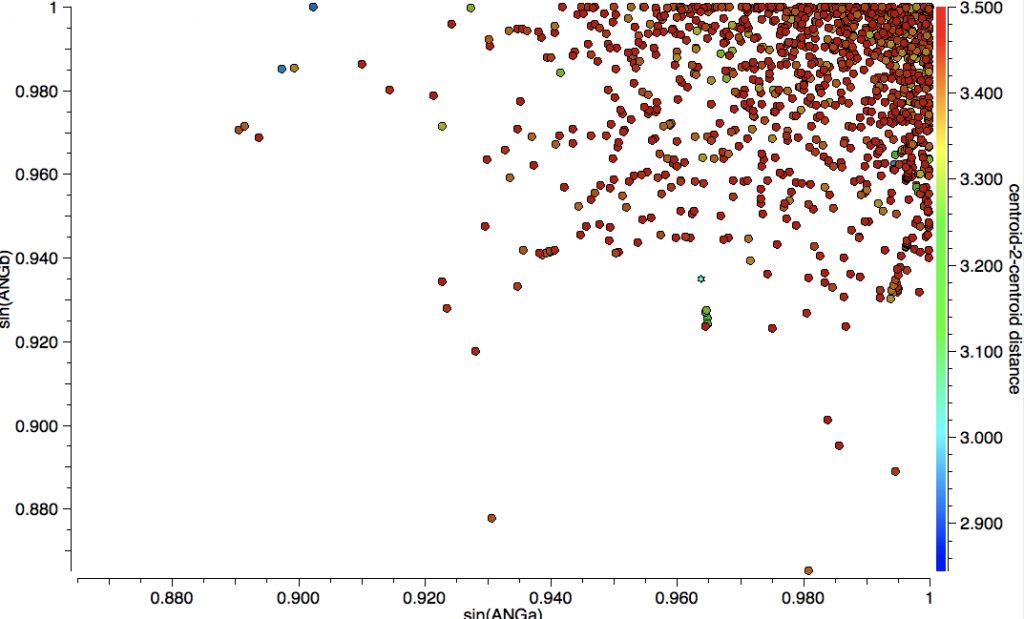
Here is another way of representing these results, in which the centroid-centroid distances (measured from the positions of 12 carbon atoms and hence statistically more reliable than any individual atom pair distance) are multiplied by either sin(ANGa) or sin(ANGb). The number of occurrences with distances < 3.2Å is less than 32 (out of 1107).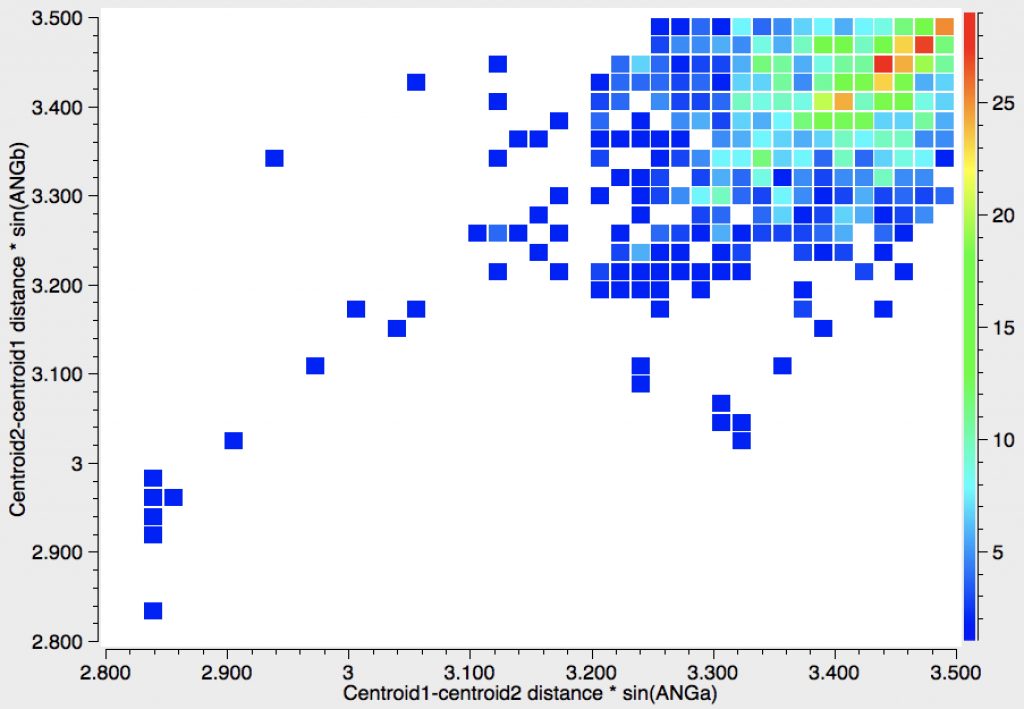
Taking a look at some of these outliers, PAZJEG has two entries, one with a short distance (dataDOI: 10.5517/ccsffzl) and one with a normal distance[cite]10.1002/zaac.200500292[/cite], which does tend to cast doubt on the former.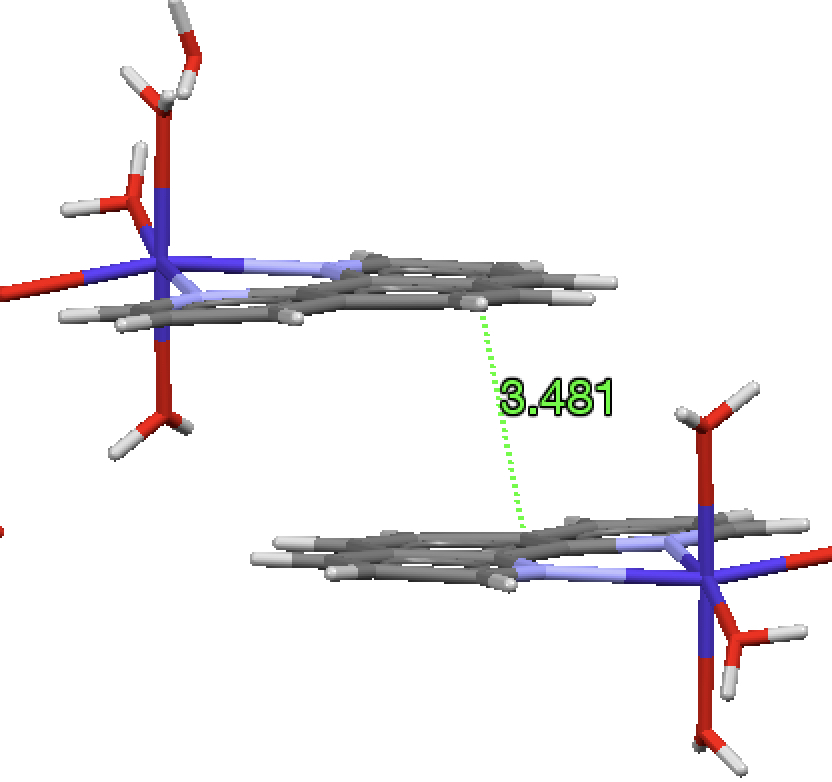
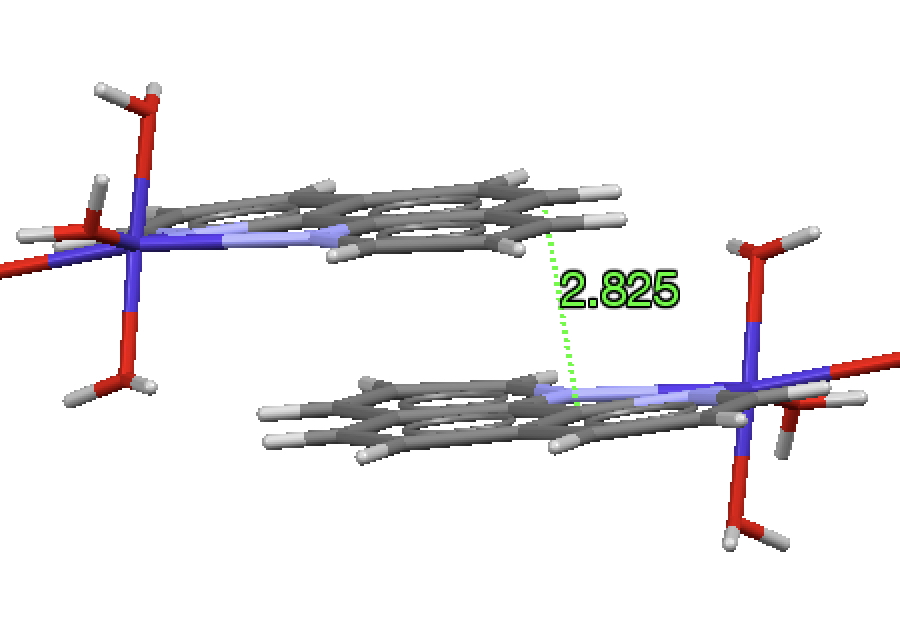
ZOMSEB[cite]10.1039/C4RA07127A[/cite], DataDOI: 10.5517/CCZS2MF) appears to have the planes of the molecules stacked ~2.5Å apart.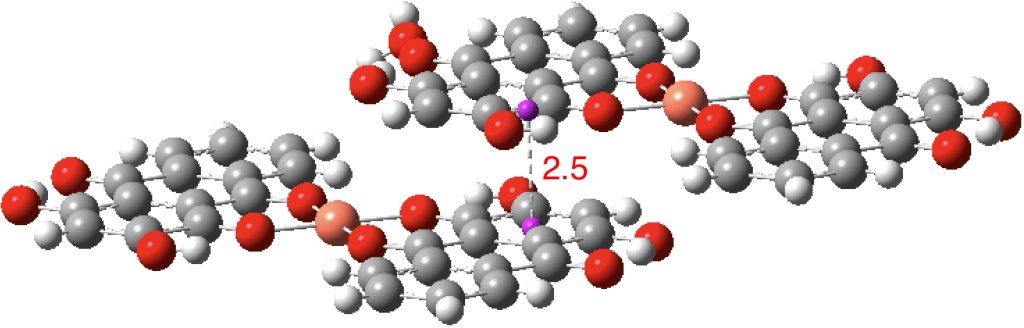
OXUDES02[cite10.1016/j.poly.2016.09.046[/cite], DataDOI: 10.5517/CCDC.CSD.CC1MBBFQ) has a separation of ~2.6Å.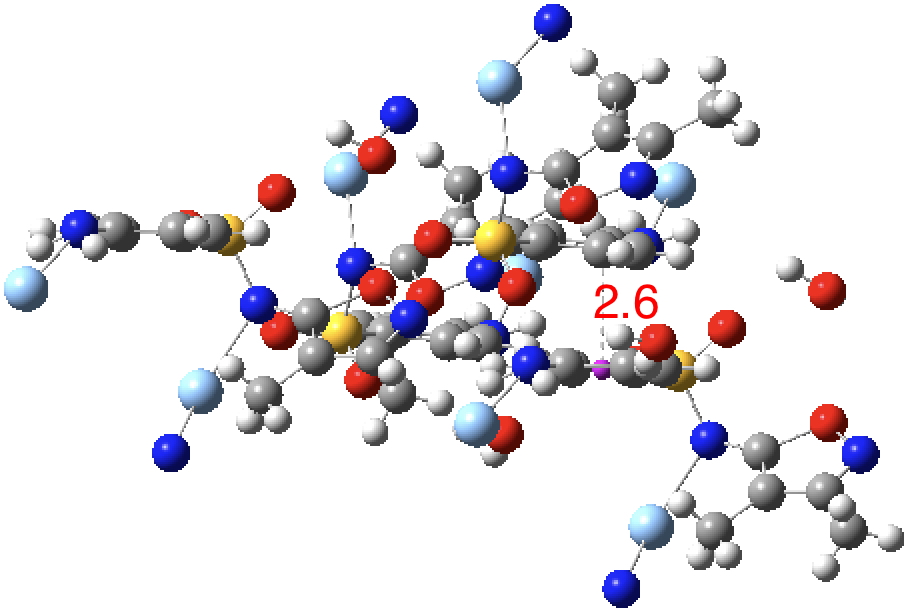
Verifying these and other outliers would require expert inspection of the crystallographic data and its refinement. This might require access to the hkl structure factors, data which are now being “strongly encouraged”‡ for deposition with the CSD, but which are not present for most structures deposited before ~2016. In extreme cases, the original diffraction images collected by the cameras would allow for a fully independent re-analysis, data which however is rarely if ever deposited.
So the separation of π-π stacked six-membered benzenoid rings is only infrequently less than ~3.2Å in measured crystal structures. There are hints it might reach as short as ~2.6Å, but such examples with values significantly less than 3.2Å do require expert validation before they can be called real.
‡See structuredepositioninformation/ “We strongly encourage data to be deposited either with imbedded structure factor data or with an associated FCF or HKL structure factor file.”
Tags: Carbon, chemical bonding, Chemistry, Cyclopentadienyl anion, Graphite, Hydrogen bond, Intermolecular forces, Nature, Organic chemistry, search query, Stacking, Supramolecular chemistry, VDW
I have repeated the search using all twelve angles, six at each centroid (each such search takes about 12 hours on my laptop!). I present below the mean of the sines of six angles at one of two rings, with the colour code indicating the centroid-centroid distance.
For examples where the mean sine at each centroid is close to 1.0, the centroid-centroid vector is exactly perpendicular to the plane of both rings. Where the means are < 1.0, the centroid-centroid vector is inclined wrt the ring planes and when the values for both rings are ~equal, it indicates that the two rings are dislocated but co-planar.
Another view of the data is shown below in which the mean of the sine of all twelve angles is plotted against the centroid-centroid distance. Another interesting candidate for inspection emerges, ringed in red (dataDOI: 10.5517/cc13skn3)