Henry Rzepa's Blog

Enols are simple compounds with an OH group as a substituent on a C=C double bond and with a very distinct conformational preference for the OH group. Here I take a look at this preference as revealed by crystal structures, with the theoretical explanation.

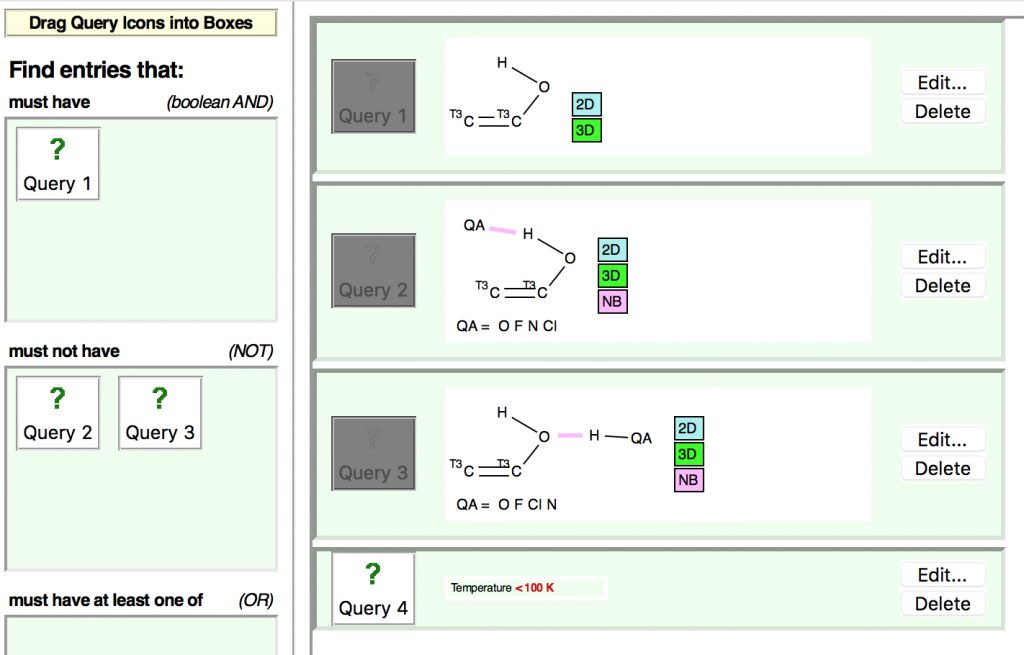
First, a search of the Cambridge structure database (CDS), using the search query shown below (DOI: 10.14469/hpc/2429)

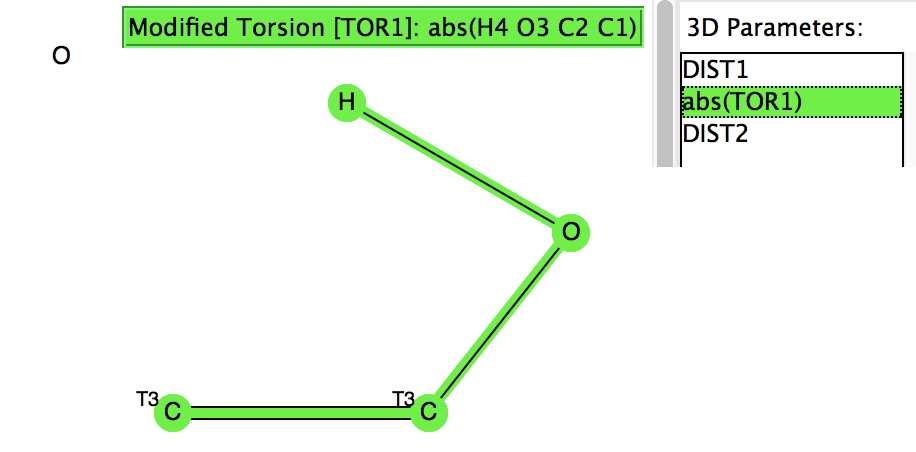
The first search (no errors, no disorder, R < 0.05) is unconstrained in the sense that the HO group is free to hydrogen bond itself. The syn conformer has the torsion of 0° and it has a distinct preponderance over the anti isomer (180°). There is the first hint that the most probable C=C distance for the syn isomer may be longer than that for the anti, but this is not yet entirely convincing.
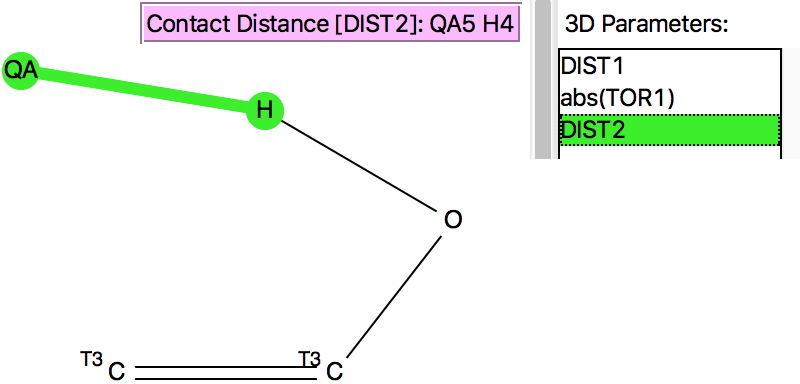
To try to make it so, a constrained search is now performed, in which only structures where the HO group has no contact (hydrogen bonding) interaction are included. This is achieved using a “Boolean” search;

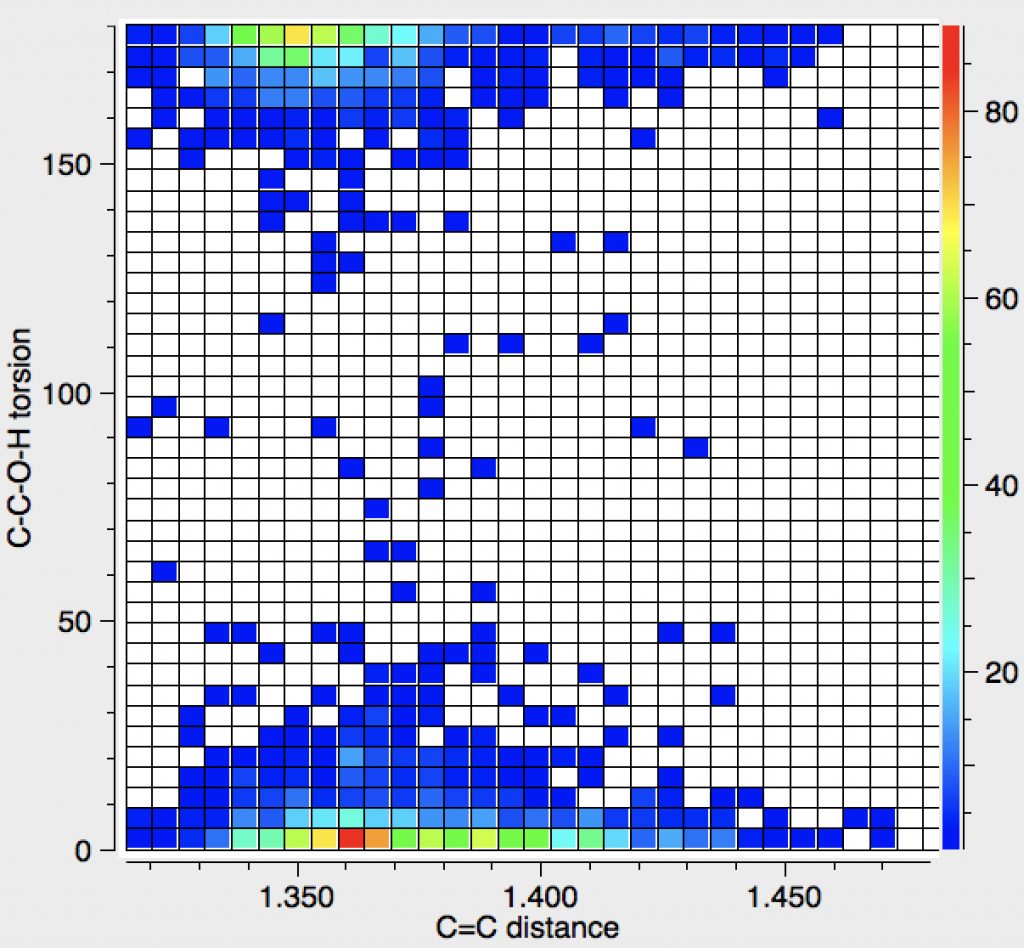
The number of hits approximately halves, but the proportion of syn examples increases considerably. There is an interesting double “hot-spot” distribution, which amplifies the lengthening of the C=C bond compared to the anti orientation.

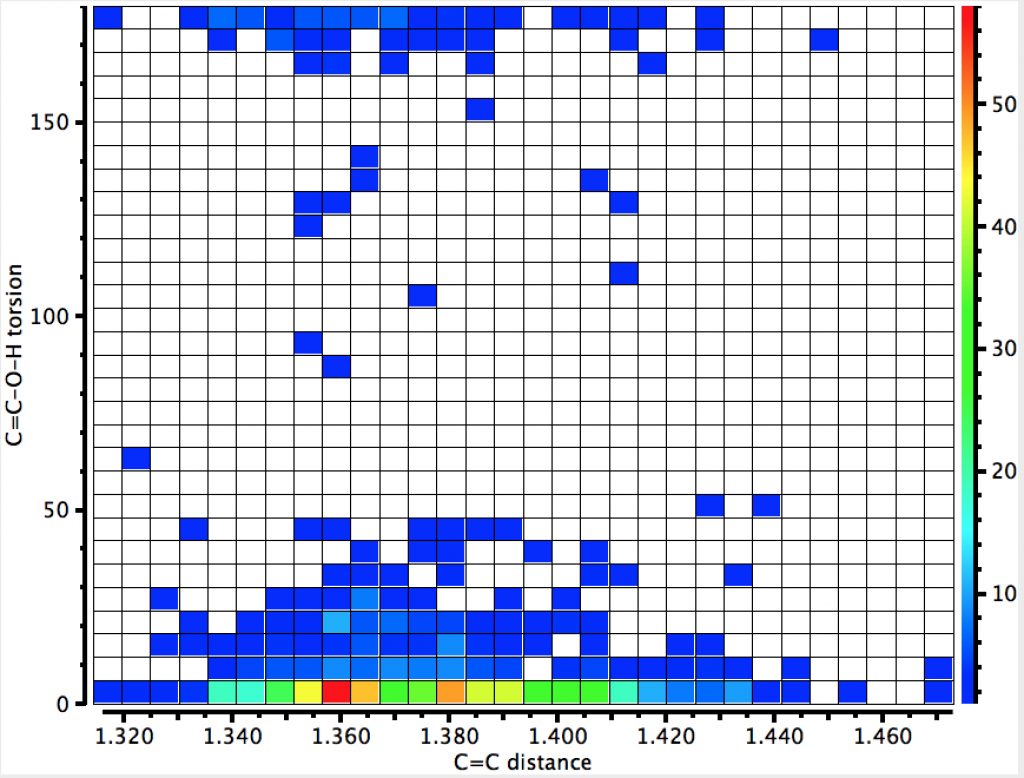
The next constraint added is that the data collection must be <100K (to reduce thermal noise) which reduces the hits considerably but now shows the lengthening of the C=C bond for the syn isomer very clearly.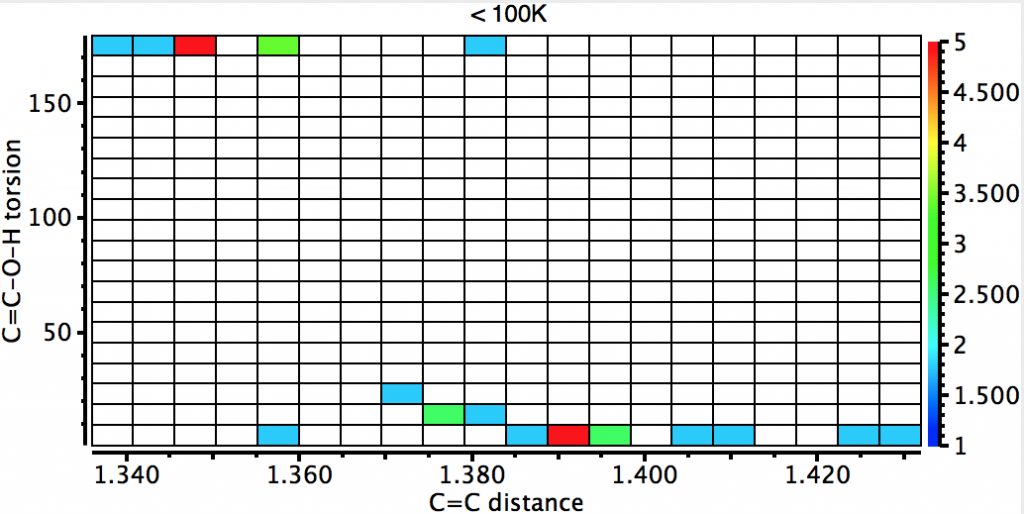

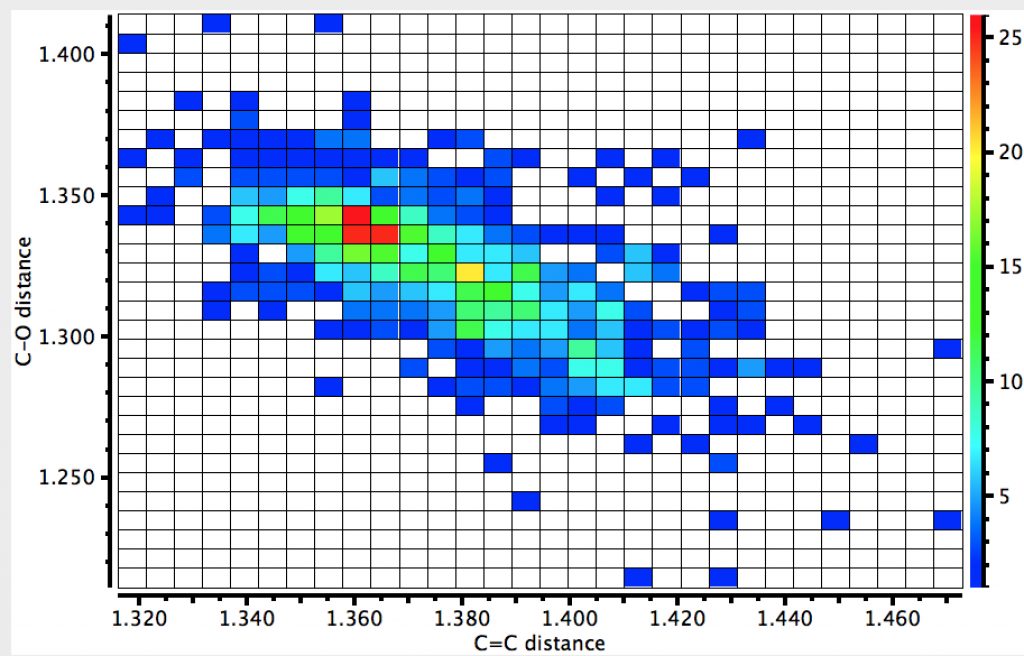
A final plot is of the C=C length vs the C-O length (no temperature, but HO interaction constraint). If there were no correlation, the distribution would be ~circular. In fact it clearly shows that as the C=C bond lengthens, the C-O bond contracts.

Now for some calculations (ωB97XD/Def2-TZVPP, DOI: 10.14469/hpc/2429) which reveal the following:

1. The free energy of the syn isomer is 1.2 kcal/mol lower than that of the syn. The effect is small, and hence easily masked by other interactions such as hydrogen bonding to the OH group. Hence the reason why removing such interactions from the search above increased the syn population compared to anti.
2. The syn C=C bond length (1.325Å) is longer than the anti (1.322Å). 
3. The syn isomer has one unique σ_O-Lp/σ^*_C-C NBO orbital interaction (below) with a value of E(2) 7.7 kcal/mol, which is absent in the anti form. As it happens, a π_O/π^*_C=C interaction is present in both forms but is also stronger in the syn isomer (E(2)= 46.8 vs 44.2 kcal/mol).
   

   unoccupied NBO, σ*C-C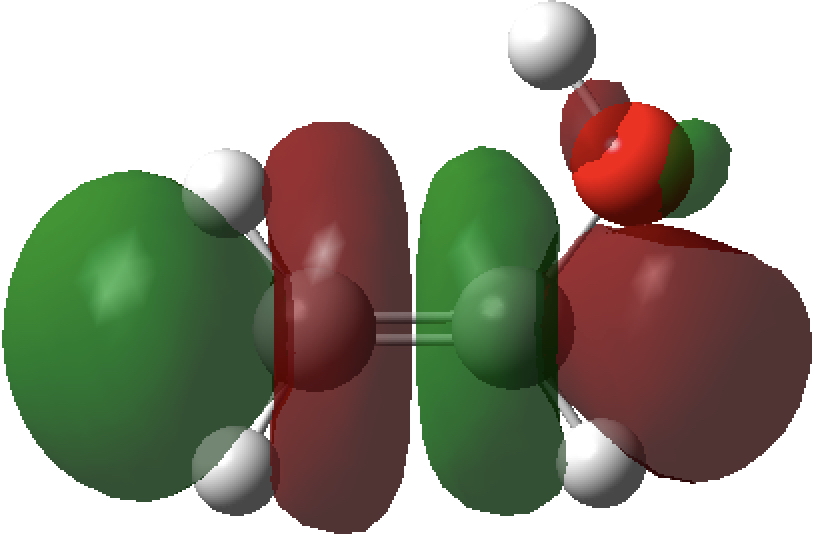
   Occupied NBO, σO-Lp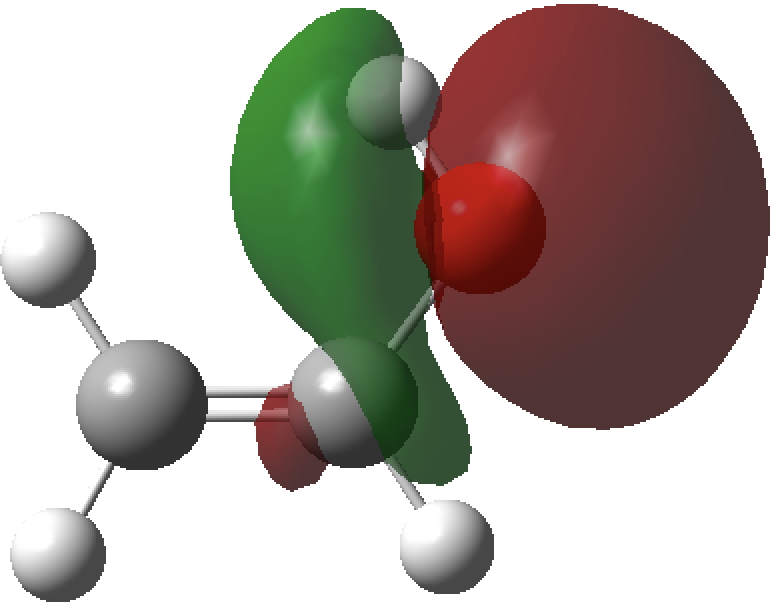

4. The overlap of the filled σ_O-Lp with the empty σ^*_C-C orbital is shown below (blue overlaps with purple, red overlaps with orange).
   
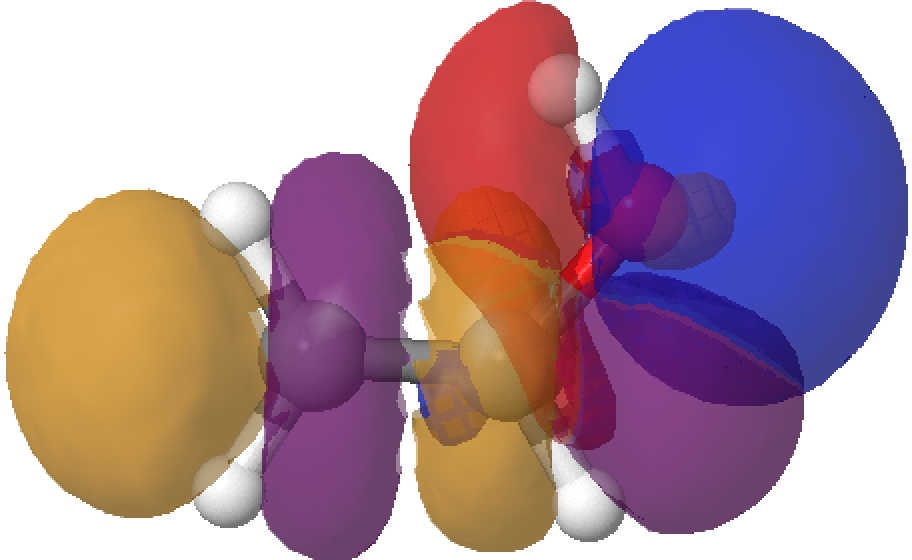
   To view the overlap in rotatable 3D, click on any of the colour diagrams above.^‡

It is nice to see how experiment (crystal structures) and theory (the calculation of geometries and orbital interactions) can quickly and simply be reconciled. Both these searches and the calculations can be done in just one day of “laboratory time” and I think it would make for an interesting undergraduate chemistry lab experiment.

---

^‡ This visualisation uses Java. Increasingly this browser plugin is becoming more onerous to activate (because of increased security) and some browsers do not support it at all. The macOS Safari browser is one that still does, but you do have to allow it via the security permissions.

---

Tags: Chemical bond, chemical bonding, Chemistry, Conformational isomerism, constrained search, Enol, free energy, Gauche effect, Hydrogen bond, Isomerism, Java, Physical organic chemistry, search query, Stereochemistry, Supramolecular chemistry

This entry was posted on Thursday, April 6th, 2017 at 11:12 am and is filed under crystal_structure_mining, reaction mechanism. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.