Here is a third candidate for the C&EN “molecule of the year” vote. This one was shortlisted because it is the first example of a metal-nitrogen complex exhibiting single, double and triple bonds from different nitrogens to the same metal[1] (XUZLUB has a 3D display available at DOI: 10.5517/CC1JYY6M). Since no calculation of its molecular properties was reported, I annotate some here.
Firstly, the 14N spectra were recorded, and so it is of interest to see if the chemical shifts reported can be replicated using calculation (ωB97XD/Def2-TZVPP/SCRF=thf). The method selected is not in the least “optimised” for this nucleus; it is often the case that various permutations of functional and basis set must be probed for the best combination for any particular nucleus. Another limitation of the calculation is that it has been done without the (rather large) counterion in place; a full model should certainly include this. The shifts below are referenced with respect to the internal N≡N signal reported at 310 ppm. The calculations have DOI: 10.14469/hpc/1980 (N2) and 10.14469/hpc/1983 (CrN123).
| Nucleus | N-Cr | N=Cr | N≡Cr |
|---|---|---|---|
| N(obs,thf), ppm | 214 | 560 | 963 |
| N(calc,thf), ppm | 213;223 | 558 | 1093 |
The match is reasonable for three nitrogens; less so for the Cr≡N variety (DOI: 10.14469/hpc/1982) but no doubt could be improved by playing with the method as noted above and probably also correcting for spin-orbit coupling perturbations of the N nucleus by the Cr nucleus. The 14N shifts of quite a number of other intermediates in the synthesis of this molecule are reported and having a method to hand which can be used to check if the structural assignment matches that calculated for it is always useful.
Next, I have a look at the nature of the Cr-N bonds themselves. The observed lengths are Cr-N: 1.863 (1.862) 1.881 (1.873); Cr=N 1.736 (1.714); Cr≡N 1.556 (1.518)Å. Calculated values in parentheses. To put this into context, I show CSD (Cambridge structure database) searches (search query DOI:10.14469/hpc/1981) for the three types of CrN bond. Firstly the triple bond (65 examples) which reveals the most probable value of ~1.54Å. This matches fairly well with the above values.
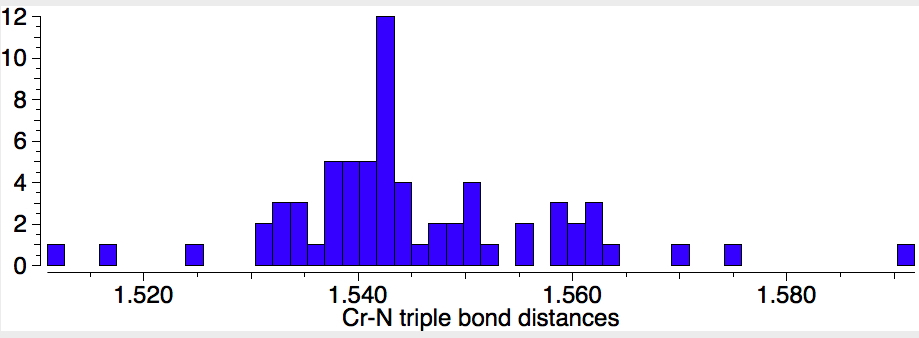
Next, Cr=N (50 examples) with a most probable value of 1.65Å. The value reported for CrN123 (1.736Å) is quite a bit longer for this bond. Again a caveat; the searches specified the bond type exactly, and this does then depend very much on how each entry in the CSD was indexed, by humans perceiving the structure and assigning the bond type on the basis of their expert chemical knowledge. It is quite likely that these integer assignments are at best informed estimates and at worst poor guesses.
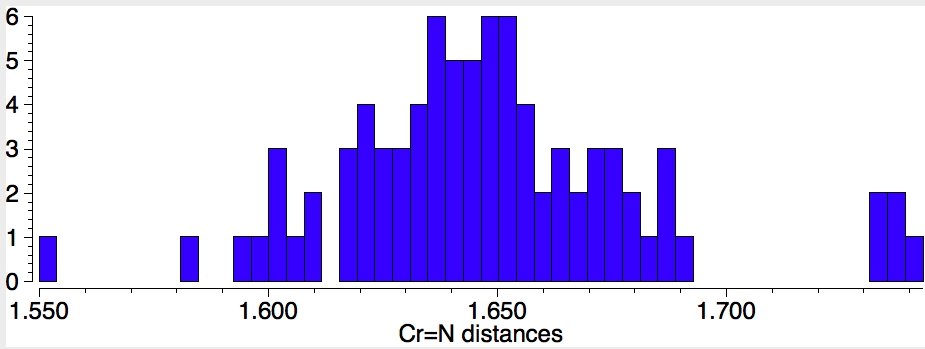
Finally, Cr-N (1398 examples) with the most probable value of 2.07Å which is a fair bit longer than the two values for CrN123. There are relatively few examples in the region of 1.87Å, which is where the CrN123 values come.
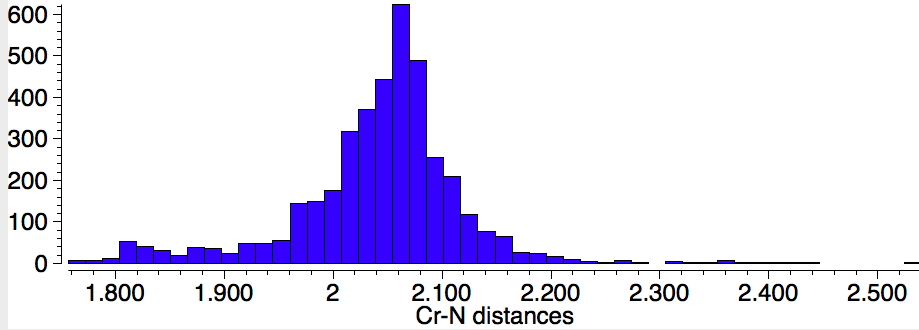
If one repeats this search, but limiting the N atom to carrying two carbons as well as a bond to Cr (as in NPri2) one gets the surprise of a bimodal (perhaps even trimodal) distribution, with an additional cluster at lengths of 1.82Å, in closer agreement with CrN123. Again I remind of the caveat that “single” bonds are often assigned by human curators on the basis of perceived chemistry. It would nevertheless be interesting to tunnel down to the possible explanation of this bimodal feature.
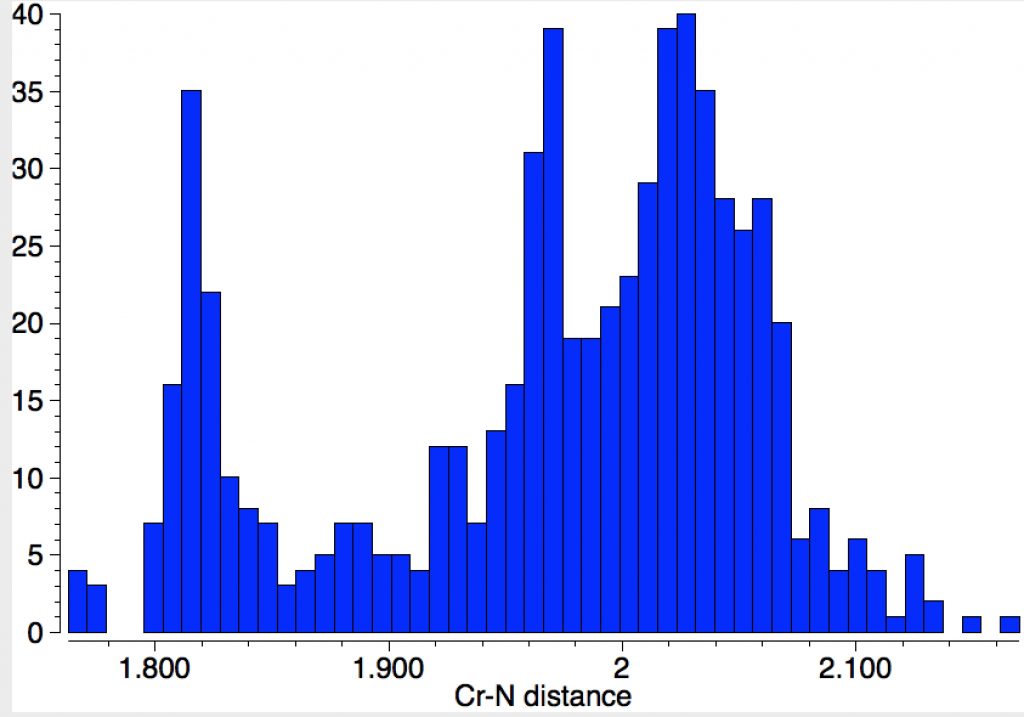
These comparisons suggest that in CrN123, the three types of bond are not isolated but may be interacting electronically in a complex manner to increase the bond order of the nominal Cr-NR2 “single” bonds (Cr=N(+)R2) whilst decreasing that of the nominal Cr=N “double” bond.
Try try to quantify the bond properties a bit more, I tried the ELF basin population technique. ELF (electron localization function) is one method of partitioning the electron density in the molecule into well defined regions or basins (which we call bonds). The results (DOI: 10.14469/hpc/1984) came out Cr-N 4.05 and 4.01e, each comprising two basins which is often typical of a bond with significant π character. The integration for a single bond is of course 2.0. The Cr=N bond was 5.07e in two basins and that for the Cr≡N 3.26e (far removed from ~6.0 in a triple bond). The valence shell total is 16.4e. These values could be said to be “challenging”, perhaps hinting that the bonding and electron density distribution in this molecule is not quite what it seems. Certainly worth a more detailed look with other methods of bond partitioning.
Well, with M123 synthesized, are there any prospects of a M1234 complex being discovered? (quadruple bonds to N HAVE been suggested!).
References
- E.P. Beaumier, B.S. Billow, A.K. Singh, S.M. Biros, and A.L. Odom, "A complex with nitrogen single, double, and triple bonds to the same chromium atom: synthesis, structure, and reactivity", Chemical Science, vol. 7, pp. 2532-2536, 2016. https://doi.org/10.1039/c5sc04608d
Tags: 10.14469, chemical shifts, expert chemical knowledge, metal, metal-nitrogen complex exhibiting single, search query
What were the values of the following at the Cr≡N line critical point:
* Density
* Laplacian
* ELF
* |lambda_1| / lambda_3
My guess is the density was well over 0.1, probably close to 0.2; the Laplacian was negative but small, with magnitude less than ~0.2; the ELF was low, near or below 0.6; and the lambda ratio was below one.
In order words, I would bet the C≡N bond has strong charge-shift character.
A full QTAIM analysis is available at DOI: 10.14469/hpc/1985.
I reproduce here the data relevant to the “Cr≡N” bond.
Type = (3,-1) BCP Cr1 N10 Rho = 3.4073546280E-01 GradRho = -7.2890912056E-15 -2.3979028398E-15 3.0012450858E-14 HessRho_EigVals = -6.5202680332E-01 -6.4311868517E-01 1.8613466408E+00 HessRho_EigVec1 = 9.7278581680E-01 6.7455915866E-02 2.2166969581E-01 HessRho_EigVec2 = -8.3848933072E-02 9.9433111002E-01 6.5383484620E-02 HessRho_EigVec3 = -2.1600257185E-01 -8.2190893979E-02 9.7292730761E-01 DelSqRho = 5.6620115236E-01 Bond Ellipticity = 1.3851437302E-02 V = -7.9145188918E-01 G = 4.6650108864E-01 K = 3.2495080055E-01 L = -1.4155028809E-01 Vnuc = 4.5249205212E+01 Ven = -1.5418008879E+01 Vrep = 1.4626556990E+01 DelSqV = -4.2358364749E+00 DelSqVen = -2.5620152134E+01 DelSqVrep = 2.1384315659E+01 DelSqG = 3.1371896243E+00 DelSqK = 1.0986468506E+00 Stress_EigVals = -4.1471432845E-01 -4.1190963540E-01 3.5172074671E-02 Stress_EigVec1 = -1.1928270549E-02 9.9676312086E-01 7.9504699586E-02 Stress_EigVec2 = 9.7329241578E-01 -6.6559816580E-03 2.2947237589E-01 Stress_EigVec3 = -2.2925878336E-01 -8.0118529708E-02 9.7006259151E-01 -DivStress = -4.9928331656E-02 -1.7422480055E-02 2.1275714125E-01 ESP = 8.3145605669E-01 ESPe = -4.4417749155E+01 ESPn = 4.5249205212E+01 BPL = 2.8695176531E+00 = 1.5563609481E+00 + 1.3131567049E+00 GBL_I = 2.8691355993E+00 GBL_II = 2.8691389353E+00 GBL_III = 2.8691370893E+00 = 1.5561464702E+00 + 1.3129906191E+00 GBL_IV = 2.8691404254E+00 = 1.5561464210E+00 + 1.3129940044E+00Specifically, ρ(r) = 0.34, which is high. The Laplacian is +0.566, but this must come with a strong caveat. It is not a homonuclear bond, and the +ve values for Laplacians indicating charge shift bonds are always derived for homonuclear combinations. Part of the unusual value for this Laplacian probably originates because the bond is heteronuclear.
Remind me, what does |lambda_1| / lambda_3 signify?
Ah, wow, 0.34 for the density, that’s *huge*. In combination with the significant positive Laplacian (even given the heteronuclear system), it *screams* charge-shift bond to me. I don’t see the ELF reported in that data summary, but it’s surely well below 0.8, and probably between 0.5 and 0.6.
The lambda ratio (called ‘epsilon’ or ε by the authors of MultiWFN) has been used as a diagnostic for ionic (non-shared) vs covalent (shared) interactions, where epsilon > 1 indicates covalent and < 1 indicates ionic. With heteronuclear bonds, where the Laplacian is not always a consistent indicator of charge-shift character, I have tentatively found this epsilon value to be much more reliable. (I haven’t run proper VB computations to establish the charge-shift character in all cases I’ve examined, though.) In other words, if an LCP has high density but epsilon < 1, it’s likely a charge-shift bond, even if the Laplacian is negative.
Here, ε = 0.35, which to my mind strongly corroborates the conclusion that this Cr≡N bond is a charge-shift bond.
I really need to download and learn a VB software package, so that I can properly test my hypotheses about ε. Either that, or I need to figure out how to implement Shaik’s MO-based method for rigorously diagnosing CSB character (10.1021/ct500367s) in ORCA.
Indeed, MultiWFN finds the ELF at the C≡N LCP to be 0.5114.
I’m generating the ELF basins now; I expect the integrated electron density for the basin to be well below the ~6 electrons expected for a ‘standard’ triple bond, probably between 2.0 and 3.0.
The Cr≡N ELF integrated density is reported as 3.26e above. MultiWFN should give the same value as Topmod (the program I used) but its integration is rather more efficient I recollect and so may differ.
Ah, indeed, I had forgotten you’d included those numbers in the original post – my apologies!
MultiWFN calculates the C≡N ELF basin at 3.18e (“high” grid generation setting), substantially in agreement with the Topmod value. I had to aggregate three of the attractors reported by MultiWFN with default settings in order to obtain the complete basin.
The Cr-N and Cr=N ELF basins are … funny. For comparison, the basin for the N-Ph bond at the “Cr=N” nitrogen looks fairly typical, neatly contained between the N and C atoms:

The basins for the (nominal) Cr-N bonds are not so well localized to the bonding region. Here are the basins for one of the Cr-N bonds:
As can be seen, the basins spread significantly to the far side of the nitrogen atom. The two basins for the other Cr-N bond are similarly spread out. For the pair of basins shown above, I get a total of 3.96e, similar to the ~4e reported in the original post.
One of the two basins for the (nominal) Cr=N bond is somewhat better confined to the internuclear region, but still spread around to roughly “even” with the nitrogen:
The other basin for the Cr=N bond isn’t confined to the interior of the molecule at all — it extends to the boundary of the system:
Across both basins, I find 4.98e, similar to the 5.07e reported in the original post.
Thus, none of the Cr-N or Cr=N bonds appear to be ‘traditional’ single or double bonds, at least per the ELF topography. They tentatively appear to me to be much more like dative/coordinative interactions between the nitrogens and the chromium.
The ELF basin for the (nominal) Cr≡N bond is pretty well contained in the internuclear region:
However, it doesn’t really seem to be ‘self-contained’ in the way that the ‘standard’ nitrogen-carbon bond is, in the first image above. Instead, it appears that the basin is confined by the surrounding isopropyl and phenyl groups, as well as the basin representing the “1.5 lone pairs” (3.02e) of the Cr≡N nitrogen:
This is the first organometallic and/or metal-ligand coordination system for which I’ve examined the ELF topology in detail, so it’s possible these sorts of behaviors are the norm. It does seem a bit of a stretch to me, though, to call the “Cr-(N-iPr)” bonds ‘single bonds’, though, given their wide volumetric spread and their high integrated electron density. If I had to call them covalent bonds, I would place them as some sort of imide: Cr=N(iPr)2. That throws quite a wrench into assignment of the formal charges of the system, though.
Yes, “throwing a wrench” into the assignment pretty much sums it up; indeed a “challenging” system.
I did play around with alternative Lewis electron pair representations, and did not find any one that really represented the ELF partitioning. It also serves to remind us that a bond is not just what happens “along the line connecting the two nuclei” and one can often get different “personalities” depending on how that partitioning is done.
Just to add some Wiberg bond orders to the data above.
Cr-N, 0.92-0.93
Cr=N, 1.56
Cr≡N, 2.82.
re MultiWFN (https://multiwfn.codeplex.com is a very powerful code for analysing wavefunctions, but it can be a challenge installing it on e.g. macOS (see https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:multiwfn). In particular, some of the dependencies need to be reinstalled each time the operating system is updated. Currently, with macOS Sierra I have not yet gotten it working.
Is it required to copy the libraries into /usr/bin/lib? I got MultiWFN working on my Debian Linux server, and it sufficed to leave the libraries in a custom location and just export those locations to the LD_LIBRARY_PATH environment variable.
Clearly, MacOS requires much more registration of libraries and applications than Linux does — but if LD_LIBRARY_PATH were to work, it seems it would eliminate a couple of the steps?