Is asking a question such as “what is the smallest angle subtended at a chain of three connected 4-coordinate carbon atoms” just seeking another chemical record, or could it unearth interesting chemistry?
A simple search of the Cambridge structure database for a chain of three carbons, each bearing four substituents (sp3 hybridized in normal paralance) reveals the following distribution:
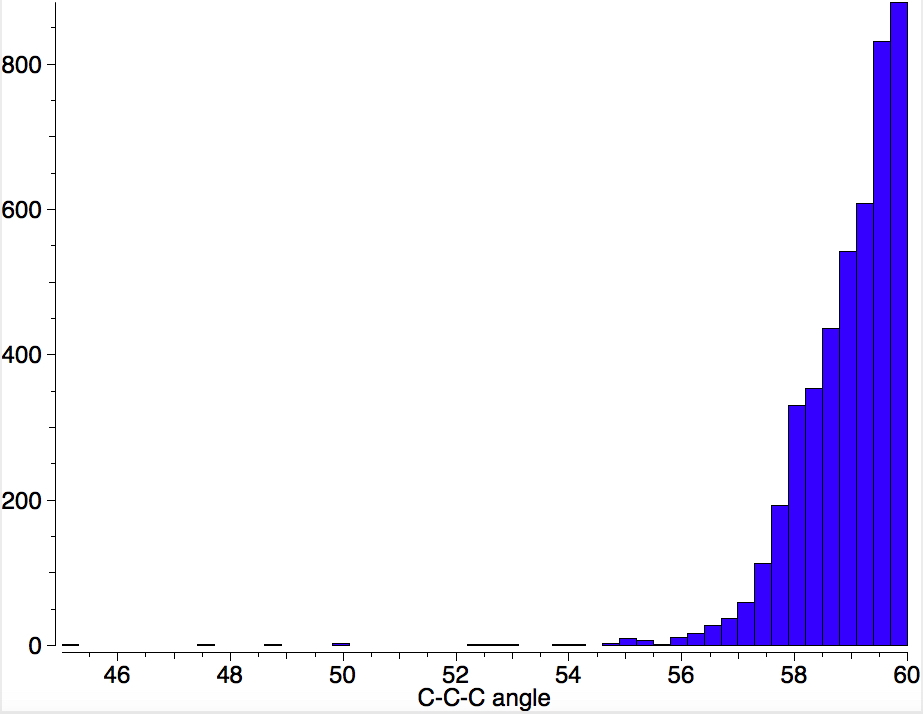
The value 60° is of course a three-membered cyclopropane ring. The tail of the distribution is very small, and there are a few small outliers with values of < 54°. Most of the time such outliers are in fact simple errors, but here we see that they are in fact semibullvalenes, of the type shown below, with the small angle subtended at the central of the three carbon atoms coloured in red.
In this diagram I have added my own semantic interpretation of what is going on. Let me itemise this:
- These molecules can undergo very rapid [3,3] sigmatropic rearrangements, shifting a σ-bond away from the 3-ring to create another such ring.
- This process elongates one of the C-C bonds and of neccessity this reduces the angle at the associated carbon.
- I have drawn two types of arrow connecting the two structures. The first is an equilibrium arrow, which implies a transition state connecting the two species. This transition state will have equal bond lengths for the forming/breaking C-C bond, and the transition state will have a rate constant which is slower than the time taken for one molecular vibration (~10-15s)
- It is also possible however that the second arrow is the correct one, and this implies an electronic resonance rather than a nuclear motion. This would have a rate constant comensurate with electron dynamics (~10-18 s) rather than nuclear vibrations.
What does x-ray crystallography measure? Well the diffraction of photons by electrons. In order to obtain a diffraction pattern, enough photons have to be diffracted to be measured, and even with most modern instruments this still takes minutes or hours. During this period, all the various nuclear positions encountered as a result of vibrations or equilibria are sampled. So if the rate constant for the [3,3] sigmatropic rearrangement is fast, x-ray diffraction will measure the average of the two sets of nuclear positions, which can be distinguished only with some difficulty (if at all) from the structure implied instead by electronic resonance.
If the equilibrium arrow applies, then the small angles of <54° are merely the average of the normal value for a 3-membered ring and a smaller value for a structure where one of the C-C bonds has been removed. In my opening sentence, I noted that the three carbon carbon atoms had to be connected in a chain. This is no longer true; the goalposts have been moved (a lot)!
If its an electron resonance, then the three carbon atoms are still connected, albeit one of the two C-C bonds is no longer a single bond but rather weaker and hence longer. The goalposts have merely been slightly shifted!
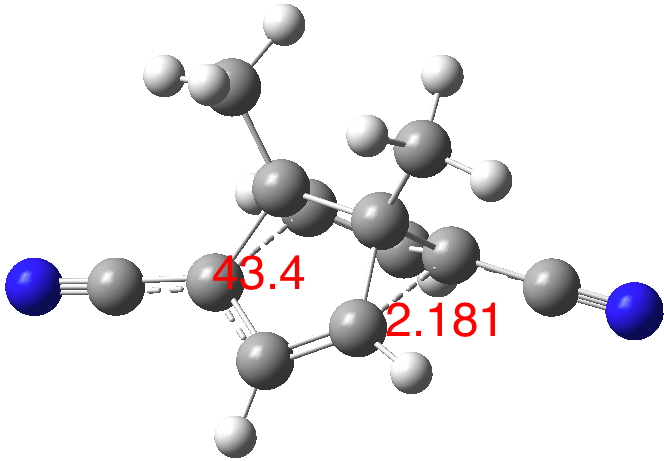
A calculation (B3LYP/Def2-TZVPP+D3 dispersion, doi: 10.14469/hpc/1850, [cite]10.14469/hpc/1850[/cite]) of the structure KUZFUE [cite]10.1021/ja00186a064[/cite] shows the C2-symmetric species shown below, with an elongated C-C bond and hence a reduced C-C-C angle, as being a true minimum (a resonance) rather than a transition state (an equilibrium). The vibration which shortens one C-C bond and lengthens the other has the real calculated wavenumber 244 cm-1.‡ But the boundary between the two possibilities (often referred to as the boundary between a single and a double minimum in a potential energy surface) is notoriously difficult to capture using calculations.
How could experiment definitively settle the issue? Well, the SLAC beam is a unique instrument. Its source of X-rays is so intense that you can get an analysable diffraction pattern from a crystal on a timescale so short that during this period no nuclear motions occur (not even vibrations). Those nuclear positions capture the true equilibrium positions of the atoms in the molecule. Now, how does one get beam time on the SLAC?
‡ Click on the image above to see an animation of this normal mode. If you are running the macOS Safari browser, make sure Preferences/Security/Plug-in settings/Java has the site ch.ic.ac.uk or ch.imperial.ac.uk set to on. If you do not do this, the somewhat unhelpful message You do not have Java applets enabled in your web browser, or your browser is blocking this applet. will appear. Note also that new system installations might tend to switch these settings to off.
Tags: animation, Bicyclic molecule, chemical record, Chemistry, City: Cambridge, Cycloalkane, Cyclopropanes, Java, Molecular geometry, Organic chemistry, potential energy surface, Safari, Web browser, X-ray
I noted in the post that if one accepts that a “half-bond” (the average of a single bond and no bond) constitutes “connected carbon atoms”, then by the same criterion, the atoms associated with the “half bond” are also connected. Thus the C-C bond length of ~2.18A must count as amongst the longest lengths between two 4-coordinate connected carbon atoms.
Roald Hoffmann has sent me the following comment:
“On small angles: not quite at C, but you might look at this series at S: ethylene sulfide, sulfoxide, sulfone. I think you will see an interesting evolution, and small angles. They can be analyzed as Walsh complexes of ethylene.”
Being urged to look at the evolution of 3-ring thiranes, here are some searches (doi for Conquest search query: 10.14469/hpc/1913)
1. 2-coordinate S, angle subtended at C; the angles are fairly normal.
2. 2-coordinate S, angle subtended at S: there is a good (albeit unsurprising) correlation between the length of the C-C bond and the angle at S. What is perhaps a surprise is the considerable variation in the C-C bond length.
3. 3-coordinate S, angle subtended at S; few crystalline examples but again much variation in the C-C length.
4. 4-coordinate S, angle subtended at S; observe the increase in the C-C bond length compared to 3-coordinate S.
Roald Hoffmann sent the following comment:
“I forgot that we published an explanation a few years ago! Here it is, basically a Dewar-Chatt-Duncanson or Walsh argument. doi: 10.1021/ja00804a017“
In the previous comment, Roald noted a 1973 study by his team rationalising the unusually long C-C distance in thiirane dioxides (sulfones). In passing, this article notes the same effect for thiadiaziridines, in which nitrogens replace the carbons of the previous example. So I thought I would conduct a search for molecules containing unusually long N-N bonds.
Four examples with N-N distances >1.6Å were found (cf. the 1.67Å noted in Roald’s article)
1. 1.63Å, doi: 10.5517/CCQLRHJ (with Hf as the third atom in a 3-ring)
2. 1.83Å, doi: 10.5517/CCQLWTZ
3. 1.66Å, doi : 10.1016/S0022-328X(00)98992-7 (with B as the third atom in a 3-ring)
4. 1.66Å, doi: 10.1248/cpb.47.601
Of these, the second is indeed extreme. The reason for this long bond is however not the same as analysed by Roald in the thiirane dioxides.
Indeed, molecule 2 is a beast of a different color. It is connected to the general weakness of N-N bonds flanked by lone-pair bearing substituents. As, for instance in the NO2 dimer, where NN is 1.78Å. We recently had a paper on the dimerization of the parent aminoxyl radical H2NO, DOI: 10.1021/acs.jpca.5b12674, and found an NN-bonded weak minimum with NN over 2Å.
Completing the homology started in the previous comments here, there are 47 O-O distances > 1.50Å (R < 0.05, no errors, no disorder).
The longest of these has O-O 1.56Å, doi 10.1021/ja9910614 and the next 1.54Å doi 10.5517/CC6WP1S
Again, the reasons for such long distances seem well worth exploring!