Clar islands are found not so much in an ocean, but in a type of molecule known as polycyclic aromatic hydrocarbons (PAH). One member of this class, graphene, is attracting a lot of attention recently as a potential material for use in computer chips. Clar coined the term in 1972 to explain the properties of PAHs, and the background is covered in a recent article by Fowler and co-workers (DOI: 10.1039/b604769f). The concept is illustrated by the following hydrocarbon:

Clar islands in a polybenzenoid hydrocarbon
The Clar islands are shown in red, and represent in effect the resonance form of this species which maximises the number of aromatic electronic sextets possible to achieve via a cyclohexatriene resonance form. It encapsulates the concept that maximum stabilization is achieved when the π-electrons in the molecule cluster together (or localize) in cyclic groups of six (rather than eg other allowed values as predicted by the 4n+2 rule of aromaticity). As a historical note, although Clar popularized the concept in the 1970s, the (C) representation had in fact been introduced almost one hundred years earlier, by Henry Armstrong (DOI: 10.1039/PL8900600095). Many demonstrations that Clar islands are reasonably based in quantum mechanical reality have been made; a very graphical and convincing one is that by Fowler and coworkers in the reference noted above, using the calculated magnetic response property known as π current densities (although this shows that the six outer islands tend merge into a single continuous outer periphery).
- Current density maps showing Clar islands for the molecule above (taken from DOI: 10.1039/b604769f)
Previous posts on this blog have mentioned the application of another computed quantum mechanical property known as ELF, the electron localization function introduced by Becke and Edgecombe in 1990 (DOI: 10.1063/1.458517 ) and subsequently adapted for use with DFT-based wavefunctions. ELF is normally applied to help analyze the bonding in a molecule; the value of the function is normalized to lie between 1.0 (a simple interpretation is that this is the value associated with a perfectly localized electron pair) and 0.0. ELF has no association with magnetic response (the latter being an excitation phenomenon), but since the Clar islands can also be considered a localizing property of the π electrons, it is tempting to ask whether the ELF function can also reveal their characteristics (this question was first posed in DOI: 10.1039/b810147g).

The ELF function, as isosurfaces contoured at various thresholds. Click for 3D
The diagram above shows the ELF function computed for the π-electrons of the molecule above (B3LYP/6-31G(d), as isosurfaces contoured at various values. At the value of 1.0, no features are discernible, but at 0.95 features which resemble basins associated with each atom centre have appeared, in the region of the 2p-valence atomic orbital on each carbon atom we regard as contributing the π-electron to the system. As the ELF threshold is reduced, these objects start to merge into what are called valence basins associated with bonds in the molecule. The outer periphery is the first to start coalescing. By a value of 0.75 (click on the diagram above to see a 3D model) the basins have merged to form seven clear-cut rings which happen to coincide exactly with the Clar islands. This feature persists down to a threshold of 0.55. Below this value, the seven individual basins merge into a single basin contiguous across the top (and bottom) surfaces of the molecule. One can also conceptualize the journey in the other direction. At low ELF values, the function is continuous, but as the threshold increases, it starts to bifurcate into separated basins. The first clear-cut bifurcation is indeed into the Clar islands, and this persists across a relatively wide range of ELF values, which suggests it is a significant feature. What is somewhat surprising is the close apparent correspondence of this way of analysing the electronic properties of the π electrons with their magnetic response computed via current densities. But association with aromaticity has previously been made (DOI: 10.1063/1.1635799). Thus Santos and co-workers have shown that the value of the ELF function at the point where it bifurcates from a ring into discrete valence or atomic basins can be related to other metrics of aromaticity. Here, that value is around 0.75 for the Clar basins, which is also within the range of values that Santos et al associate with prominent aromaticity (benzene itself has a value around 0.95).

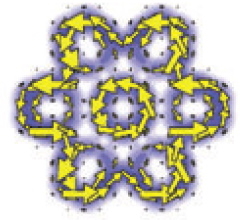
A C114 PAH
The ELF function for the 114-carbon unit shown above again reveals prominent Clar islands, the inner heptet being very similar to the picture painted using current densities.

Clar islands in the ELF function for a C114 carbon PAH
The final example involves diboranyl isophlorin (DOI: 10.1002/chem.200700046), a 20 π-electron antiaromatic system. Such systems are particularly prone to forming locally aromatic Clar islands as an alternative to global antiaromaticity (DOI: 10.1039/b810147g).

A Diboranyl isophlorin.
The ELF function is shown for both the neutral diboranyl system and its (supposedly more aromatic) dication. Here a mystery forms. No Clar islands are seen, and instead it is the periphery that bifurcates, at ELF thresholds of 0.5 for the neutral and 0.7 for the dication. The latter value clearly is that of an aromatic species, but the former is somewhat in no-man’s land, but certainly less aromatic that the dication. One for further study I fancy!

ELF Function for diboranyl molecules (red=neutral, green=dication). Click for 3D
Does the ELF function have any possible advantage over the use of current density methods for analysing aromaticity? Well, the latter is normally applied to flat systems with planes of symmetry defining the π-system, and with respect to which an applied magnetic field is oriented. How to orient this magnetic field is not so obvious for prominently non-planar or helical molecules. Since the ELF function does not depend on the orientation of an applied magnetic field, it may be a useful adjunct for studying the properties of π-electrons in non-planar systems.
Tags: aromaticity, Clar, Clar islands, Cloud Clar islands, computer chips, ELF, Henry Armstrong, Interesting chemistry, non-planar systems, pence, Santos
[…] is one further concept that can be introduced. Clar (for a discussion, see DOI: 10.1021/cr0300946) proposed that benzenoid 6π-electron local […]