The outcome of pericyclic reactions con depend most simply on three conditions, any two of which determine the third. Whether the catalyst is Δ or hν (heat or light), the topology determining any stereochemistry and the participating electron count (4n+2/4n). It is always neat to conjure up a simple switch to toggle these; heat or light is simple, but what are the options for toggling the electron count? Here is one I have contrived by playing a game with the periodic table. The ring closure of a divinylketone is called the Nazarov reaction, it being promoted thermodynamically by coordination of a Lewis acid to atom X. Divinyl ketone can be regarded as a hidden pentadienyl cation, since the C=O bond is polarised Cδ+Oδ- in the time-honoured manner of organic chemistry. In this (formal) resonance form, it becomes part of a pentadienyl cation and can electrocyclise via a 4-electron reaction involving a stereochemical process known as conrotation. The new bond is formed antarafacially (from opposite faces) at the termini of the pentadienyl cation (ωB97XD/6-311G(d,p)/SCRF=dichloromethane.[1]). Note that for the uncatalysed reaction, the barrier is high and the reaction is endothermic but adding a BF3 to the oxygen lowers the barrier and removes the endothermicity.[2]
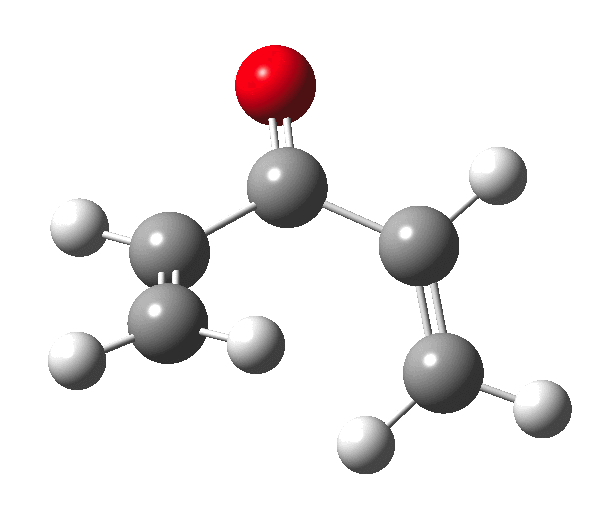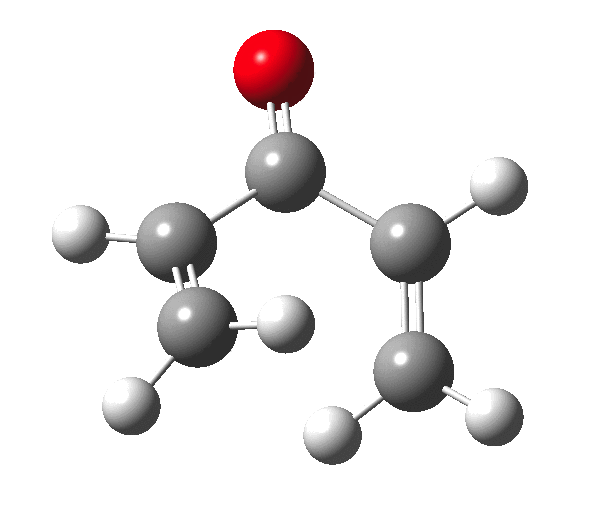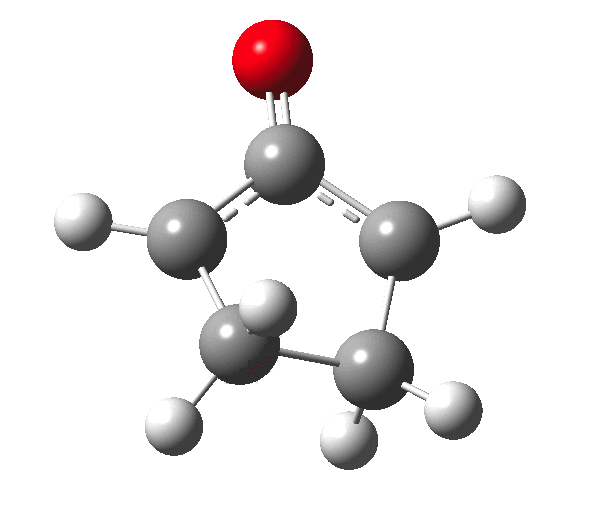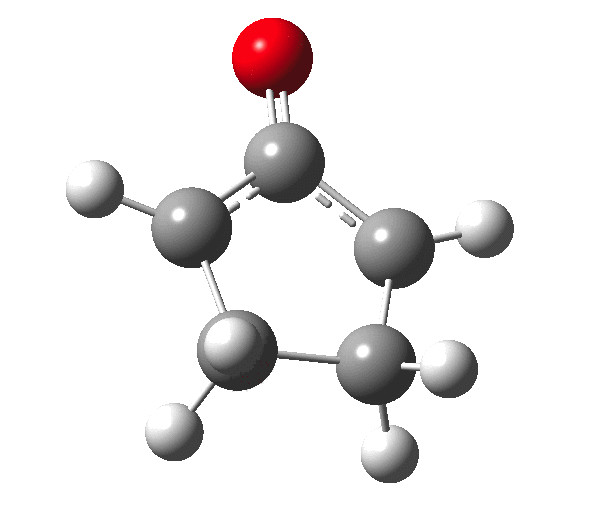
So, one can play a game and ask what would happen if the polarity of the C=X bond were to be reversed. This means going left of oxygen in the periodic table, ending at Be.[3] The reaction has a high barrier, but it is strongly exothermic.† However the most noteworthy aspect is that the stereochemistry of the electrocyclisation is now disrotatory, with suprafacial bond formation (from the bottom face in the animation below). The stereochemical outcome of this reaction has been flipped by reversing the polarity of the CX bond.‡
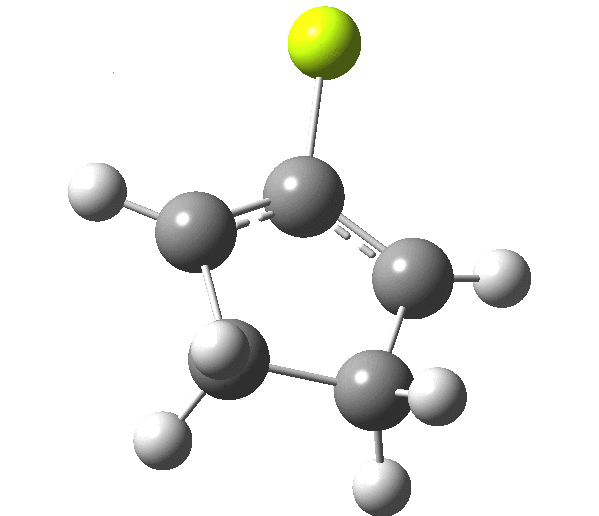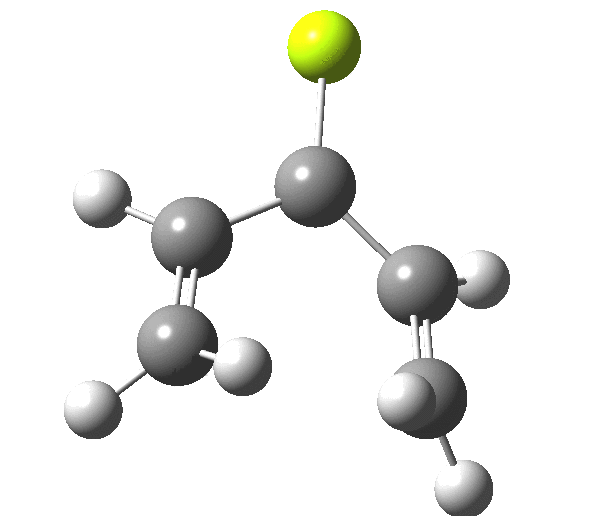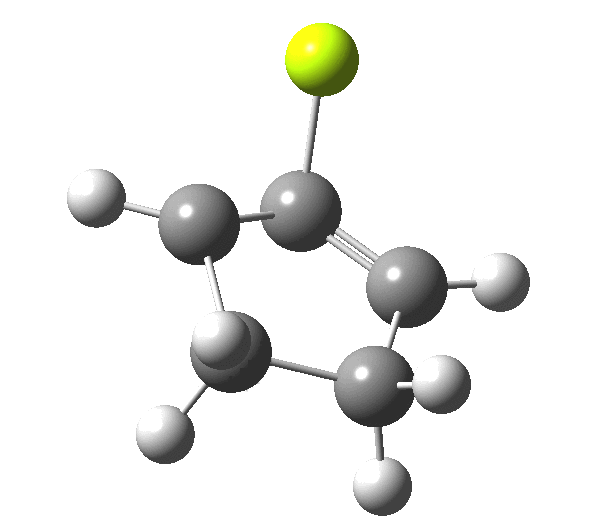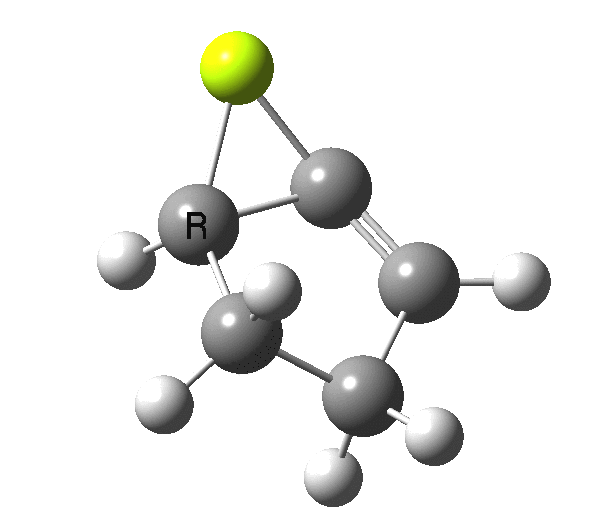
This little example shows how a thought game played using the periodic table can then be reality tested by solving appropriate quantum mechanical equations. In this instance, one is not going to rush into the laboratory to try to replicate the experiment, but it might help catalyse new thoughts amongst the readers of this blog.
‡Things are likely to get more complicated when one starts playing with the spin state of the molecule. Here it is modelled as a closed shell singlet, but open shell (triplets) may well also decide to get involved. †By virtue of a hidden intermediate (HI), which can be seen at IRC = +2, where the symmetry breaks and an unsymmetrical product forms exothermically. This really is an artefact of using just a naked Be atom in our game.
References
- Henry S. Rzepa., "Gaussian Job Archive for C5H6O", 2014. http://dx.doi.org/10.6084/m9.figshare.1125721
- Henry S. Rzepa., "Gaussian Job Archive for C5H6BF3O", 2014. http://dx.doi.org/10.6084/m9.figshare.1125724
- Henry S. Rzepa., "Gaussian Job Archive for C5H6Be", 2014. http://dx.doi.org/10.6084/m9.figshare.1125792
Tags: animation, Interesting chemistry, pericyclic