Following the discussion here of Kekulé’s suggestion of what we now call a vibrational mode (and which in fact now bears his name), I thought I might apply the concept to a recent molecule known as [2.2]paracyclophane. The idea was sparked by Steve Bachrach’s latest post, where the “zero-point” structure of the molecule has recently been clarified as having D2 symmetry.[cite]10.1002/chem.201304972[/cite]
Let me start with a ωB97XD/6-311G(d,p) calculation of this mode. Because the mode is a mixture of C and H motions (which differ according to the molecule), I am going to try to normalise the mode by reducing the mass of the all atoms except the core six to effectively zero. The mode itself looks as below with the H-weighting applied. The hydrogens are riding, massless, on each of the six carbons.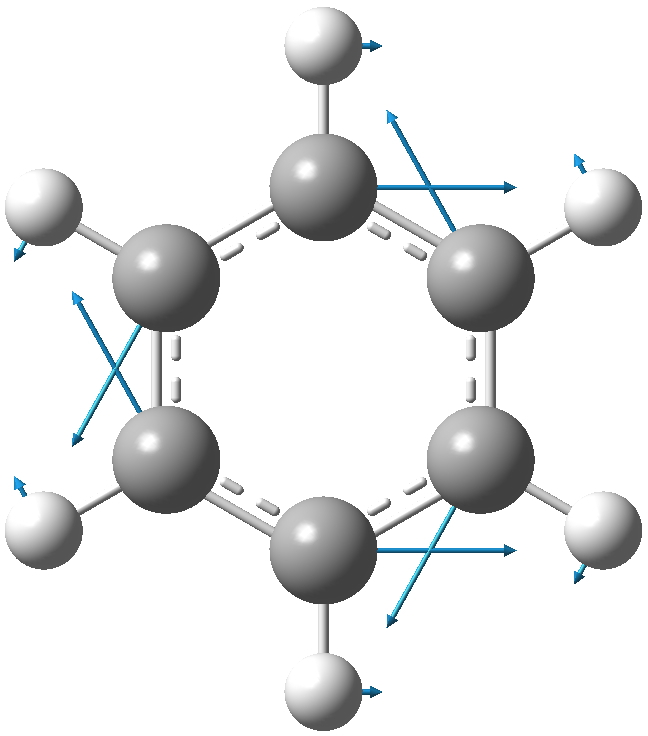
The results are presented in the table below for the paracyclophane, in three different spin states.
| System | Mass-weighted modes, s, a | Reduced mass, sym | Reduced mass, asym | DOI |
|---|---|---|---|---|
| Benzene, singlet | 1342 | 1318 | [cite]10042/30857/cite] | |
| paracyclophane, singlet | 1335, 1330 | 1257 | 1237 | [cite]10042/30858[/cite] |
| paracyclophane, singlet | 1335, 1330 | 1257 | 1237 | [cite]10042/30858[/cite] |
| paracyclophane, triplet | 1413, 1418 | 1403 | 1394 | [cite]10042/30859[/cite] |
| paracyclophane, quintet | 1566, 1563 | 1521 | 1522 | [cite]10042/30860[/cite] |
There are three effects which manifest.
- The first is that the Kekulé mode is depressed in the cyclophane compared to benzene itself. I have previously discussed how even in benzene this mode is depressed from its expected value because of the natural tendency of the π-system to adopt a localised cyclohexatriene motif (a tendency that is overcome by the σ-framework). So we conclude that this tendency (famously highlighted by Shaik, Hiberty and co[cite]10.1021/cr990363l[/cite]) is even slightly stronger in [2.2]paracyclophane. One might presume that the two π-clouds, in an enforced proximity which is certainly repulsive, co-operate to enhance the effect (see below).
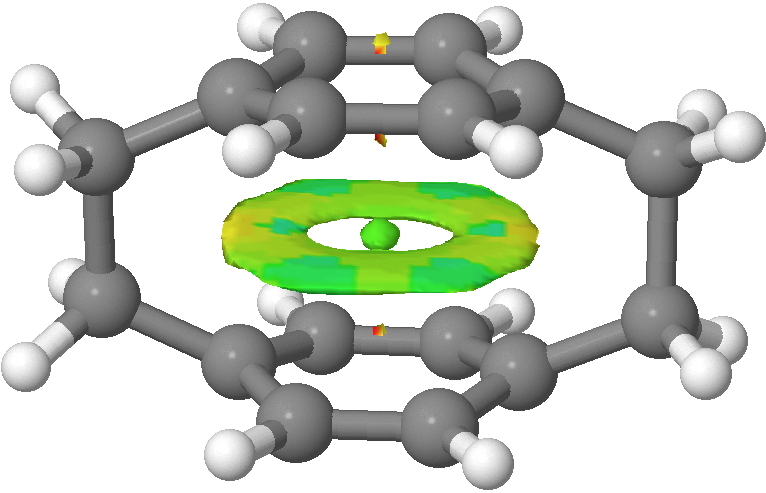
NCI surface showing π-repulsions (yellow). Click for 3D
Perhaps this cooperation would be even stronger were it not from the distinct distortion from planarity that the cyclophane bridges enforce, and which might discourage the π-tendency to form cyclohexatriene.
- The interaction between the two π-clouds splits the Kekulé mode into a symmetric and antisymmetric pair, by either 5 or 20 cm-1 depending on the mass weighting.
- As one promotes the π-electrons into antibonding orbitals (triplet, then quintet) one increasingly weakens the π-resistivity. The π-electrons no longer want to collect into double bonds and so resist the symmetrising tendency of the σ-electrons less. The splitting of the Kekulé mode also decreases.
My point with this post was to show how interesting new effects can be teased out of systems of contemporary interest by invoking Kekulé’s famous (vibrational) mode. Whether this corresponds to what the man himself had in mind is quite another matter of course.
Tags: 10.1002, 201304972, Hiberty and co, Steve Bachrach