As my previous post hints, I am performing my annual spring-clean of lecture notes on pericyclic reactions. Such reactions, and their stereochemistry, are described by a set of selection rules. I am always on the lookout for a simple example which can most concisely summarise these rules. The (hypothetical) one shown below I think nicely achieves this, and raises some interesting issues in the process.
The reaction is a hydrogen shift (as either a proton or a hydride), and the interesting issue is immediately how the nomenclature of either process should be applied.
- This cationic rearrangement is shown as a [1,2] sigmatropic proton shift. The rules declare that as a thermal process involving 4n+2 electrons (two electrons, n=0, red arrow) the shift should occur suprafacially (red hydrogen) with a plane of symmetry at the transition state.
- BUT! It could also be represented as a four electron process (4n, n=1, blue arrows) involving a [1,4] shift. There is now a conflict in the outcome. The magenta coloured resonance arrow implies the same product is formed as with the [1,2] shift. But the pericyclic rules declare that this cannot be the case. The resolution is to declare that a [1,4] shift would result in a different stereochemical outcome (blue hydrogen, an antarafacial shift from the top face of the reactant to the bottom face of the product) with an axis of symmetry.
- The anionic series involves two more electrons, an increment that inverts the 4n+2/4n assignment. Reaction 3 is still a [1,2] shift, but it now belongs to the 4n rule and so we infer it should proceed antarafacially (blue hydrogen, but a 1,2 antarafacial shift would be unprecedented).
- The anionic series can also be represented alternatively (red arrows) as a 4n+2 process, involving a [1,4] suprafacial shift.
So for both cation and anion, two different pericyclic circulations are possible, leading to different stereochemical outcomes. Which might actually occur in practice? This is where the simple selection rules have to be augmented with calculations, ωB97XD/6-311G(d,p) in this case.
- The IRC for reaction 1 is shown below.[1] It shows a smooth suprafacial migration of a hydrogen. The transition state has a Cs plane of symmetry. This calculation also reveals another important facet of pericyclic reactions; their transition states are aromatic. One can infer this from the length of the C1-C2 bond (from which the [1,2] numbering is derived), which is 1.383Å[2], which is a typically aromatic value, compared with the very non-aromatic value for the cyclobutene alkene bond of 1.332Å. The starting values for both lengths were respectively 1.509Å and 1.382Aring;. In other words, the C-C bond along which migration takes place changes from a single bond to a (delocalized) aromatic bond at the transition state, and the spectating remote C=C bond changes from that for a delocalised allylic cation to a conspicuously localised alkene.
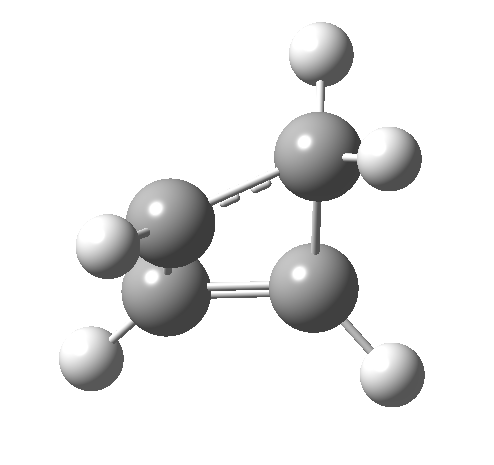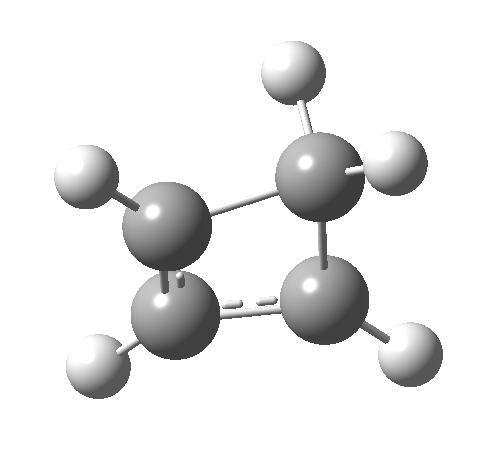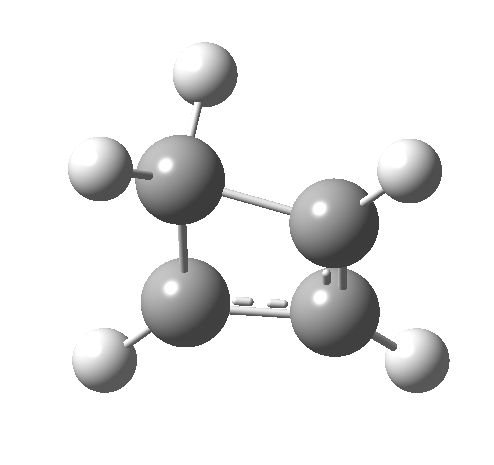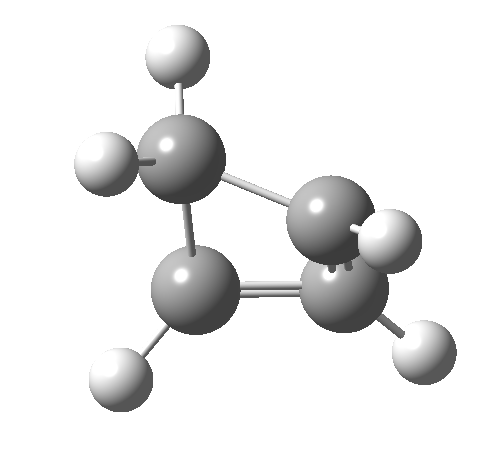
- How about the antarafacial mode, reaction 2? The stereochemistry clearly involves a migration from the bottom face of the reactant to the top face of the product. Notice the chirality indicated at the transition state (R,R), associated with the disymmetric C2 axis of symmetry present at this point.[3]‡
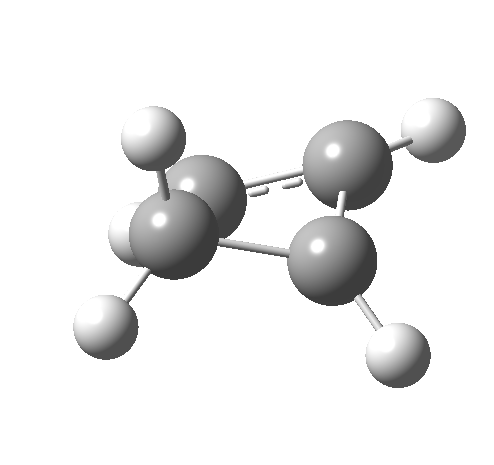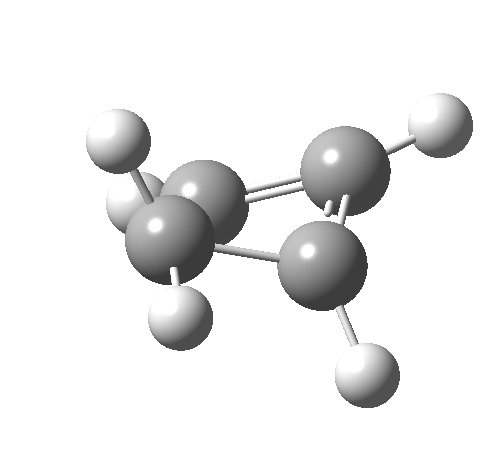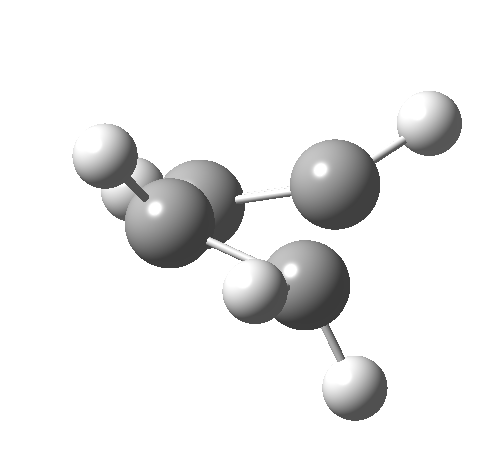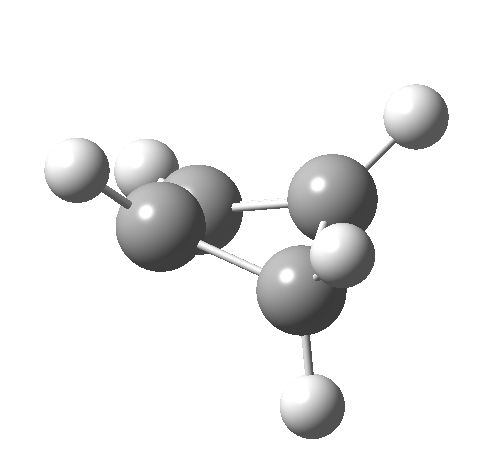 Such contortions bring a penalty, the energy of this mode is a lot higher (85 kcal/mol in free energy)† What of the bond lengths? The length of the C-C bond along which the H apparently migrates is 1.509Å at the start and 1.527Å at the transition state. This latter value is clearly NOT aromatic! As for the C2-C3 bond, it starts at 1.382Å (the same typical allylic cation) but is largely unchanged at the transition state is 1.396Å (also a typical aromatic value). So clearly it is the [1,4] shift that sustains the aromaticity, not any [1,2] shift.
Such contortions bring a penalty, the energy of this mode is a lot higher (85 kcal/mol in free energy)† What of the bond lengths? The length of the C-C bond along which the H apparently migrates is 1.509Å at the start and 1.527Å at the transition state. This latter value is clearly NOT aromatic! As for the C2-C3 bond, it starts at 1.382Å (the same typical allylic cation) but is largely unchanged at the transition state is 1.396Å (also a typical aromatic value). So clearly it is the [1,4] shift that sustains the aromaticity, not any [1,2] shift. - Now for the anionic series, with two extra electrons involved. Again, an antarafacial path is attempted.[4]‡ Although C2 disymmetric symmetry is achieved, the distortion required for the antarafacial stereochemistry across just a single bond brings a heavy toll, and the C1-C2 bond springs open. What little can be inferred is that the remote C=C bond does not seem to achieve aromatic status at the transition state, preferring localisation (1.356Å). We have pushed the system a bit too far.
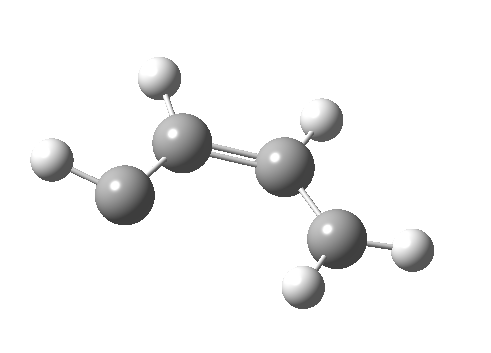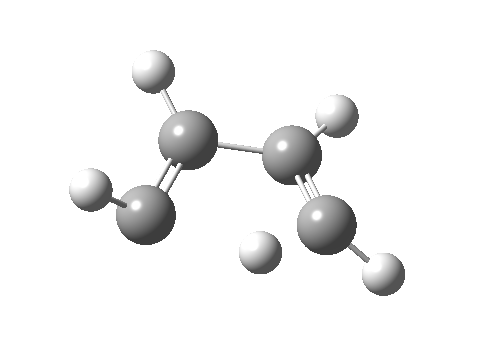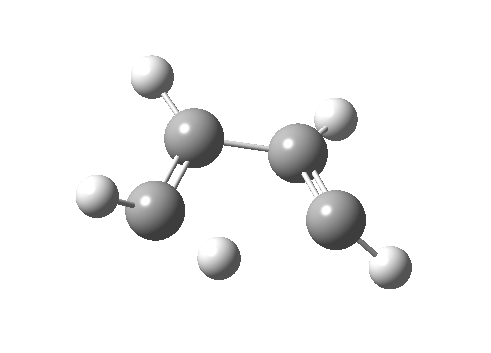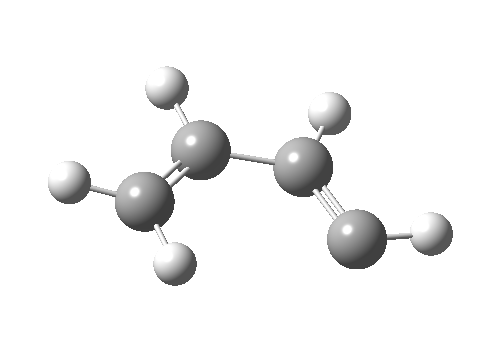
- Route 4 is again a conventional suprafacial migration[5]. The C-C length for the apparent [1,2] migration starts at 1.542Å and achieves 1.583Å at the transition state. Not aromatic then. The C2-C3 bond starts at 1.407Å (a typical delocalized allylic anion) and changes merely to 1.405Å (a very delocalized aromatic value). So we again see clear evidence of a [1,4] rather than a [1,2] shift, involving a very aromatic six electrons.
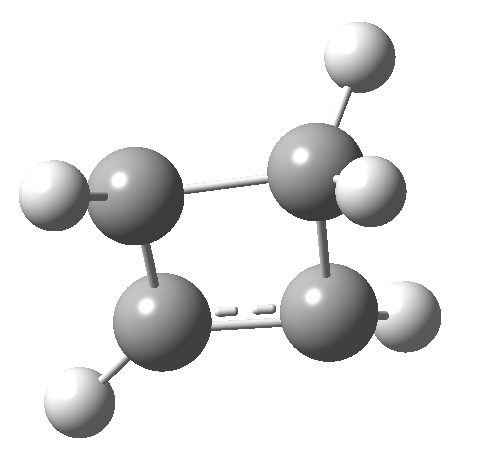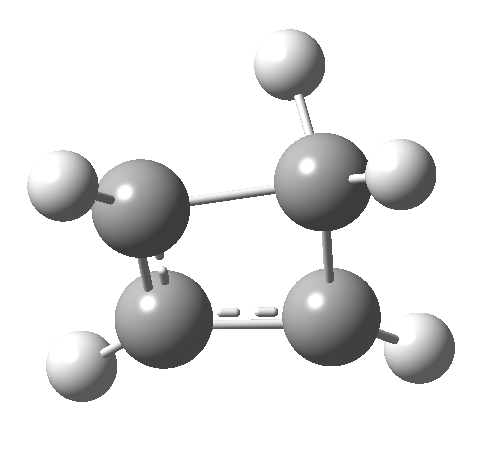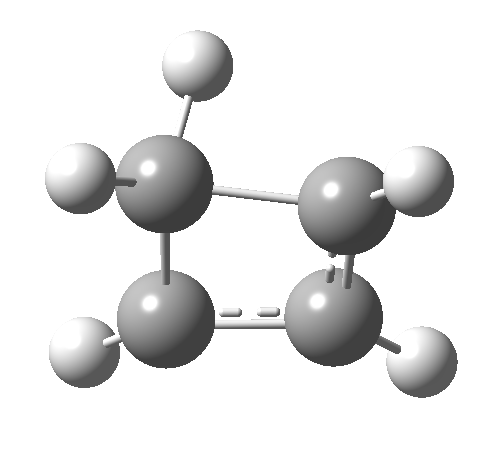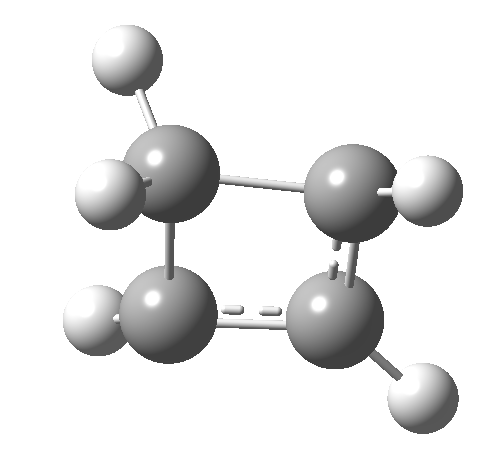
So here we have a simple reaction involving only four carbon atoms that can be used to exemplify the four thermal selection rules for pericyclic processes. It is doubtful that such an example could ever be obtained by synthesis and experiment; rather it represents a quantum mechanical experiment on the rules. And we have teased out the associated transition state aromaticities from the computed geometries.
‡This is not actually computed as a transition but as a second-order saddle point, diverting the reaction to another manifold which is not of interest here. If you want to explore this diversion yourself, get the files yourself[6].
†I am not concerned with explaining the overall reaction barriers here; in such a small ring system they are all actually too large to be feasible reactions. Rather, the point is merely to use quantum mechanics to illustrate the geometric and stereochemical characteristics of the transition states.
References
- H.S. Rzepa, "Gaussian Job Archive for C4H5(1+)", 2014. https://doi.org/10.6084/m9.figshare.892333
- H.S. Rzepa, "Gaussian Job Archive for C4H5(1+)", 2014. https://doi.org/10.6084/m9.figshare.892335
- H.S. Rzepa, "Gaussian Job Archive for C4H5(1+)", 2014. https://doi.org/10.6084/m9.figshare.892332
- H.S. Rzepa, "Gaussian Job Archive for C4H5(1-)", 2014. https://doi.org/10.6084/m9.figshare.892371
- H.S. Rzepa, "Gaussian Job Archive for C4H5(1-)", 2014. https://doi.org/10.6084/m9.figshare.892334
- H.S. Rzepa, "Gaussian Job Archive for C4H5(1+)", 2014. https://doi.org/10.6084/m9.figshare.892336