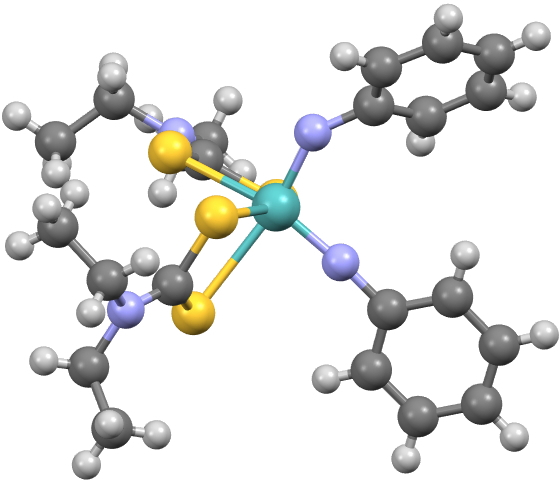
This potential example of a molecule on the edge of chaos was suggested to me by a student (thanks Stephen!), originating from an inorganic tutorial. It represents a class of Mo-complex ligated by two dithiocarbamate ligands and two aryl nitrene ligands (Ar-N:).
I focus on two specific examples[1], where R=R’ = H or Me, with crystal structures available for both. The reason for its appearance in a tutorial is that it provides a nice example of electron counting. Relocated to a tutorial on organic chemistry, it might also provide an interesting challenge for drawing a Lewis structure. So before we deal with the edge of chaos, let me start with the electron counting/Lewis structure. I have set out three possibilities for these above.
- This one is drawn with nine bonds (= 9 electron pairs = 18 electrons) associated with the Mo. This is the 18-electron valence shell rule for transition elements, originally set out by Langmuir. Of these nine bonds, six are normal, nominally covalent, shared electron bonds formed from the six valence electrons of the Mo (ground state electronic configuration [Kr].4d5.5s1) and six electron from the ligands (two from a S- pair , and four from a N= pair). Three more bonds are formed by donation of electron pairs, two from S and one from N. This last results in the creation of (nominal) positive charges on each of the S atoms and on ONE of the nitrogen atoms (note not BOTH). In particular, one of the nitrene ligands now becomes sp-hybridised and hence linear, whilst the other remains sp2 hybridized and hence bent. As a result, the Mo formally assumes a charge of 3-.
- This Lewis resonance form returns one S-Mo covalent electron pair to having lone pair status, and replaces the shared electron pair with a Mo-N bond formed from the remaining nitrogen lone pair. Both nitrogen atoms are now sp-hybridized, and hence linear.
- This form removes an electron pair from one C=S double bond, and replaces it with a N=C double bond formed from the lone pair on the Et2N group.
- Structures 1 and 3 each show the nitrogen ligands to contribute a total of five bonds (ten shared electrons) to the Mo-N bonding. In the forms shown above, one N contributes 6, the other 4. But equally one might imagine a situation where partial bond orders of 2.5 allow each nitrogen to in effect contribute 5 electrons equally. This would result in the angle at each nitrogen being “half-bent” rather than having one fully bent and the other not bent at all. So now we have set up our molecule on the edge of chaos, where it might exist in a form best described by the resonance structures 1-3, and an alternative form where the two nitrogen atoms are “half-bent”.
We can now apply the reality check of inspecting the crystal structure.
- For R=H, one Mo-N-C angle is 171° and the other is 141°, a difference of 30°.
- The consequence of the differentiated nitrogens is that the Mo-S bond immediately co-linear with the Co-N bond is 2.61A for the linear nitrogen and 2.76 for the bent nitrogen. The lone pair on the bent nitrogen can stereoelectronically align with the Mo-S bond to lengthen it. But the p-orbital on the linear sp-nitrogen is precisely orthogonal to the Mo-S bond, and hence does not interact with it.
Click for 3D
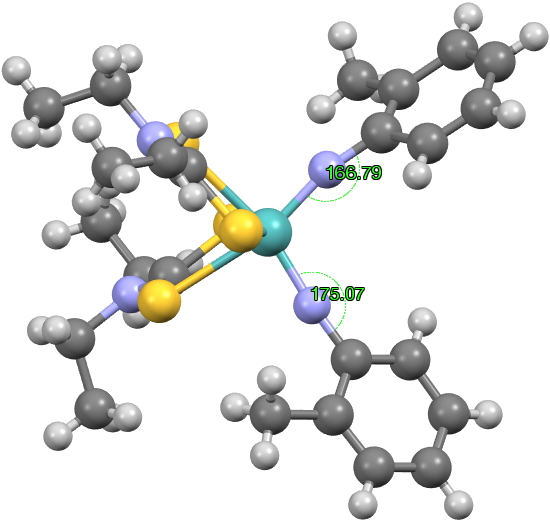
What happens with R=Me? The two angles are now 167 and 175°, a mere 8° different. The system appears to have “flipped” from 6+4 bonding heading to 5+5 bonding, all because of an apparently innocuous change on the two aryl groups.
click for 3D
With this sort of behaviour, one has to ask if it might in fact be a crystallographic artefact. One way of checking this is to calculate the geometries of the two molecules, at the ωB97XD/Def2-TZVPD level in this instance. Any errors are at least systematic, and not subject to crystallographic effects. For R=H,[2] the two angles subtended at N are 175.1 and 146.6, a difference of 28.5°, in good agreement with the crystallographic value of 30°. For R=Me, the values are 169 and 152°, a difference of 17°. It is certainly less than for R=H, but a bit more than is apparently measured (8°).
On balance, I think we probably can assign these two Mo complexes to the category of molecules on the edge of chaos, where the mere replacement of an o-H by an o-Me can have a big change on the angles at N.
References
- P. Barrie, T.A. Coffey, G.D. Forster, and G. Hogarth, "Bent vs. linear imido ligation at the octahedral molybdenum(VI) dithiocarbamate stabilised centre", Journal of the Chemical Society, Dalton Transactions, pp. 4519-4528, 1999. https://doi.org/10.1039/a907382e
- H.S. Rzepa, "Gaussian Job Archive for C22H30MoN4S4", 2013. https://doi.org/10.6084/m9.figshare.746899
Here is another example of bimodal bond angles (thanks Mark!), from doi: 10.1002/anie.201100816
The unique feature here is that at each Ru centre, one equatorial nitroso ligand is clearly bent (124°) and one axial is perfectly linear. This is replicated with a calculation (ωB97XD/Def2-SVPD), which gives one nitroso bent with angle 126.9° and the other linear (doi: 10.6084/m9.figshare.810402).
If Ru2+ is [Kr].4d6, it receives six electrons from respectively the two-electron donors axial Cl–: (obs. Cl-Ru distance 2.349Å), ether O: and bent O=N: (obs. N-Ru distance 1.915Å), requiring six more electrons to achieve an 18-electron configuration. To explain why the second nitroso group is linear, I suggest a four-electron ON=Ru bond (obs. N-Ru distance 1.727å) rather than ON-Ru, which leaves just two electrons from one of the two asymmetrically bridging chlorines (obs. Cl-Ru distances 2.392Å and a longer 2.812Å) to make up the 18. So, rather than each Ru receiving four electrons in total (two each) from the two bridging chlorines, which would require both nitroso groups to be bent as two electron donors, the molecule decides to linearise one of the NO groups instead as a four-electron donor and to downgrade one of the bridging chlorines as a donor by lengthening its bond length to the Ru.
Certainly, a further interesting example not only of bimodal angle behaviour, but of associated bimodal bond length behaviour!
Mark (in an email) has raised the possibility of a counting scheme for the nitroso complex above that starts from Ru(IV); [Kr].4d4. If one follows the (formal) covalencies outlined above, one must get to a 16-electron valence shell for Ru. The two electrons ionised from the Ru must end up on the ligands somewhere, but not in the covalent bonds to Ru. One might think this should then be reflected in the calculated partial atomic charge on Ru.
In this regard, an interesting new charge scheme has been proposed in 2012 (CM5: doi: 10.1021/ct200866d) which has been parametrised by “fitting to reference values of the gas-phase dipole moments of 614 molecular structures”. This enables, in an empirical manner, a direct correlation between partial atomic charges and the measurable property of a dipole moment.
When the CM5 analysis is applied to the complex above (doi: 10.6084/m9.figshare.810445), the Ru = +0.77. The older Hirshfeld charge is +0.15. On the face of it, this probably does not provide any overwhelming evidence for Ru(IV) involvement. But of course charge schemes are only one way of partitioning electrons! (I wonder for example if the CM5 scheme is equally successful at predicting quadrupole moments in molecules?)
The Ru(II)/Ru(IV) debate (along with others, i.e. Pd(II)/Pd(IV), Cu(I)/Cu(III) etc) can be juxtaposed with the Hg(IV) story at doi: 10.1002/anie.200703710). It may be that many of these systems exhibit multi-reference character in their wavefunctions, which makes any single-reference analysis of the charge distribution only a very approximate estimation (I should note that multi-reference character further degrades the concept of integer formal charges, and one is forced to accept non-integer formal charges as inevitable. Which rather destroys their conceptual simplicity).